968. 监控二叉树 - 力扣(LeetCode)
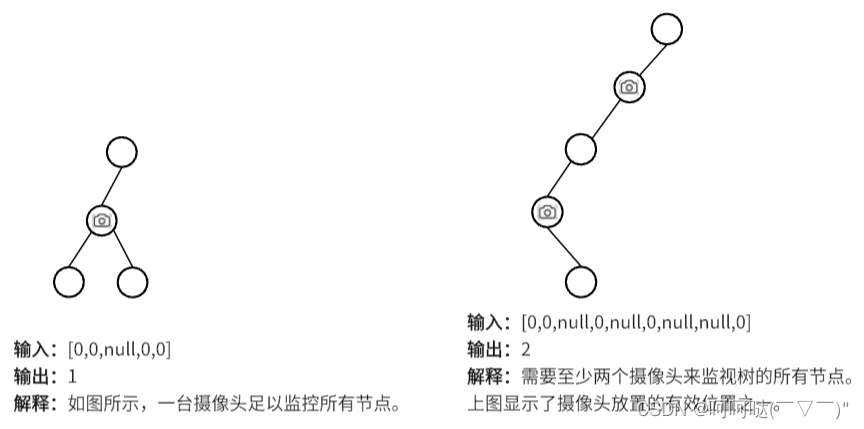
给定一个二叉树,我们在树的节点上安装摄像头。节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。计算监控树的所有节点所需的最小摄像头数量。
>>解题思路:
重要线索->题目示例中的摄像头都没有放在叶子节点上!
摄像头可以覆盖上中下三层,若把摄像头放在叶子节点上,就浪费一层的覆盖。因此把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖范围
>>思考(ˇˍˇ) 想~为啥不从头结点开始看起呢?为啥从叶子节点看起呢?
因为头结点放不放摄像头只能省下一个摄像头,叶子节点放不放摄像头省下来了的摄像头数量是指数级别的。也就说我们会从下往上看。局部最优:让叶子节点的父节点安摄像头,所用摄像头最少。整体最优:摄像头所用最少!
也就说可以用局部最优推出全局最优,且找不出反例,可用贪心!
>>难点:
① 二叉树的遍历(后序遍历:左右中,可以在回溯的过程中从下到上进行推导)
② 隔两个节点放一个摄像头
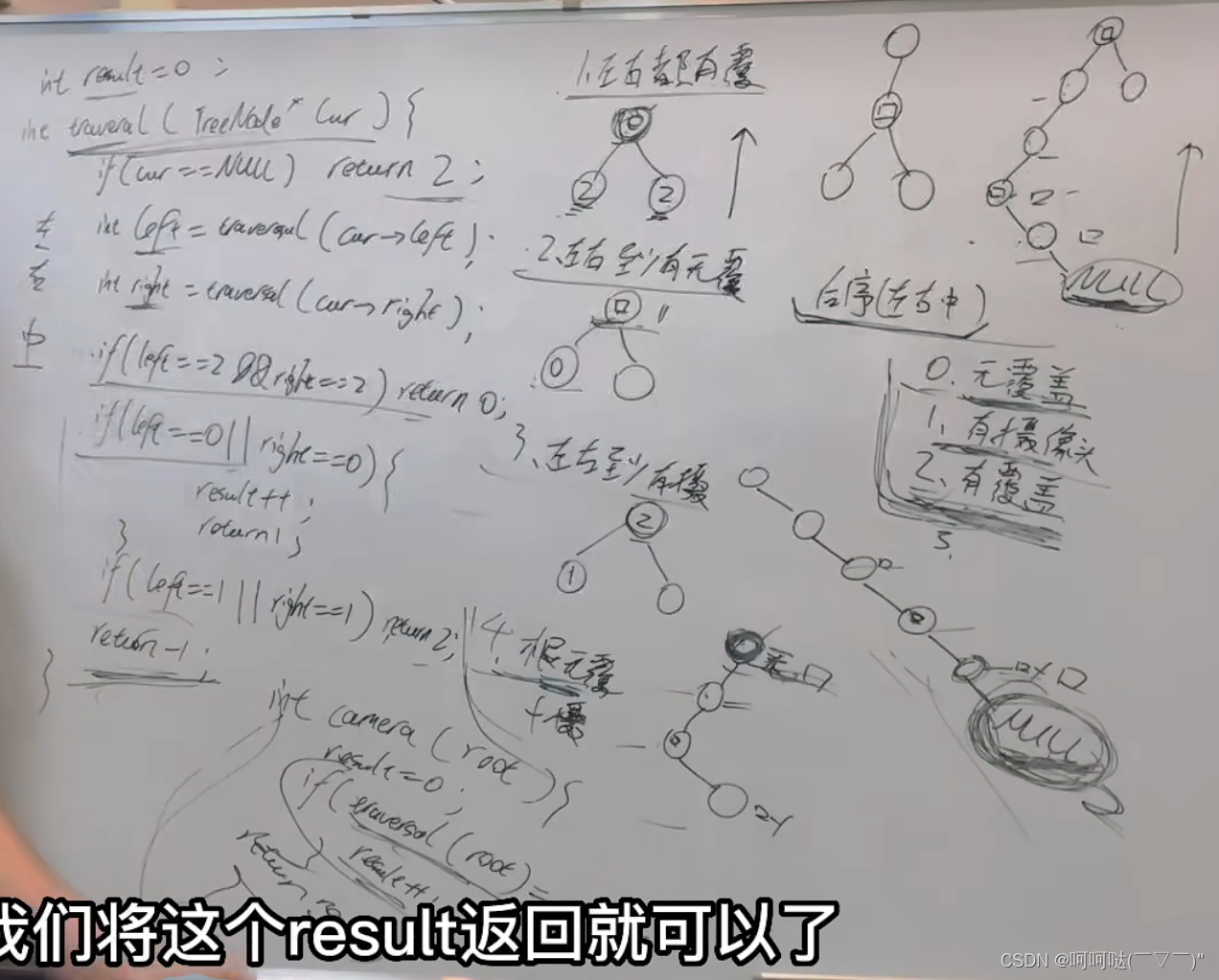
>>如何隔两个节点放一个摄像头![]()
由于本题状态转移并没有择优的过程,只是单纯的状态转移!所以不需要用动态规划的状态转移公式!!!
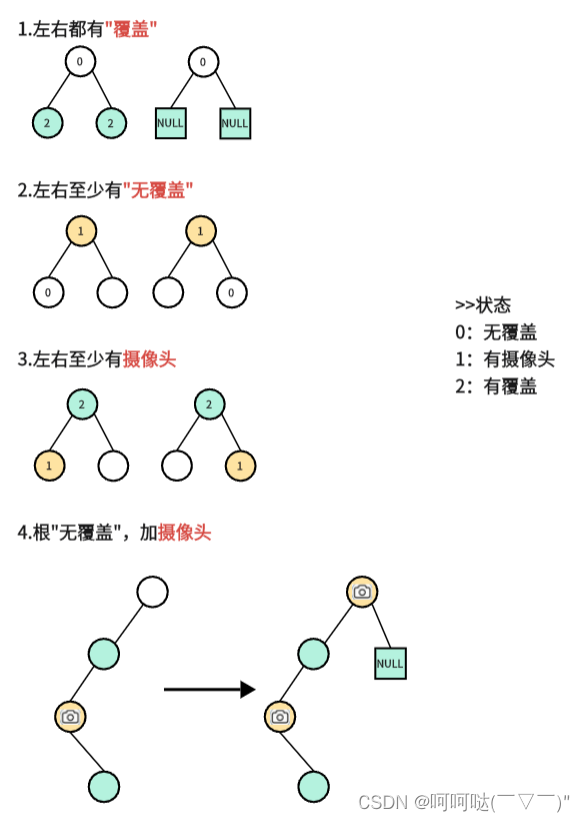
- 节点的三种状态
- 0:无覆盖
- 1:有摄像头
- 2:有覆盖
![]() 思考:为什么没有第四种状态,即无摄像头状态?
思考:为什么没有第四种状态,即无摄像头状态?
因为其实无摄像头就是 无覆盖 或者 有覆盖的状态,所以节点就一共还是三个状态。
分情况讨论
class Solution {
public:
int minCameraCover(TreeNode* root) {
result = 0;
if(traversal(root) == 0) {
result++;
}
return result;
}
private:
int traversal(TreeNode* cur) {
// 空节点,该节点有覆盖
if(cur == NULL) return 2;
int left = traversal(cur->left); // 左
int right = traversal(cur->right); // 右
// 情况1:左右节点都有覆盖
if(left == 2 && right == 2) return 0;
// 情况2
if(left == 0 || right == 0) {
result++;
return 1;
}
// 情况3
if(left == 1 || right == 1) return 2;
return -1;
}
int result;
};
// 状态
// 无覆盖:0
// 有摄像头:1
// 有覆盖:2
// 1.左右都有"覆盖",父节点就设置为"无覆盖"
// 2.左右至少有"无覆盖",父节点就设置为"摄像头"
// 3.左右至少有"摄像头",父节点就设置为"覆盖"
// 4.根节点为"无覆盖",增加一个摄像头来自代码随想录的课堂讲解截图:
参考和推荐文章:
代码随想录 (programmercarl.com)
贪心算法,二叉树与贪心的结合,有点难...... LeetCode:968.监督二叉树_哔哩哔哩_bilibili