数学建模系列文章：

以下是个人在准备数模国赛时候的一些模型算法和代码整理，有空会不断更新内容：

评价模型（一）层次分析法（AHP）,熵权法，TOPSIS分析 及其对应 PYTHON 实现代码和例题解释
评价模型（二）主成分分析、因子分析、二者对比及其对应 PYTHON 实现代码和例题解释
优化模型（零）总述，分类，解析各类优化模型及普适做题步骤
优化模型（一）线性规划详解，以及例题，用python的Pulp库函数求解线性规划
优化模型（二）非线性规划详解，以及例题，Scipy.optimize 求解非线性规划

优化类问题

(本文是在备战数模过程中，基于清风课件和一些个人理解所得到一些知识点整理)

优化问题概述

什么是数学规划

数学规划是运筹学一个分支，用来研究，在给定条件下 （约束条件） ，如何按照某一衡量指标 （目标函数） 来寻求计划，管理工作中的最优方案 ==> 求目标函数在一定约束条件下的极值问题。

一般形式

$$minZ=f(x)x:决策变量$$

$$s.t.g(x)<=0,i=1,2,3,4f(x):目标函数$$

小 demo

分 类

一些规划问题的小练习

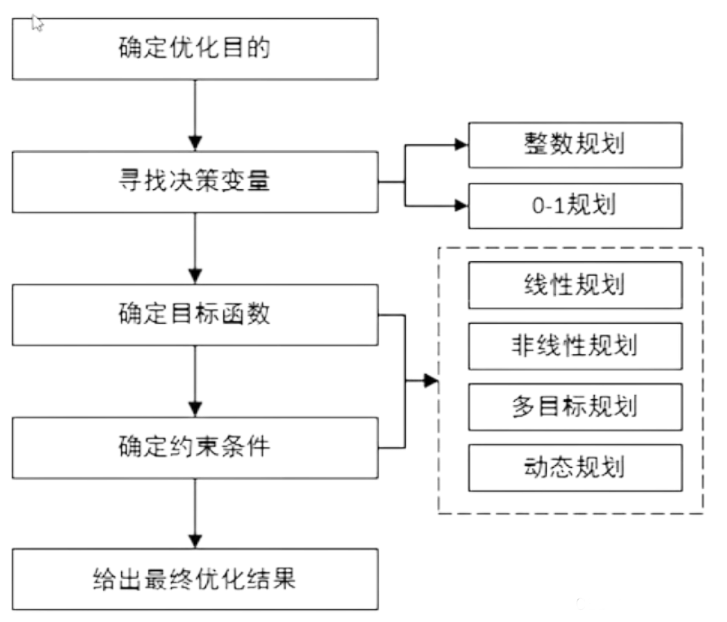
优化类问题一般的解题步骤

(1)首先确定决策变量，也就是需要优化的变量;
(2)然后确定目标函数，也就是优化的目的;
(3)最后确定约束条件，决策变量在达到最优状态时，受到那些客观限制.

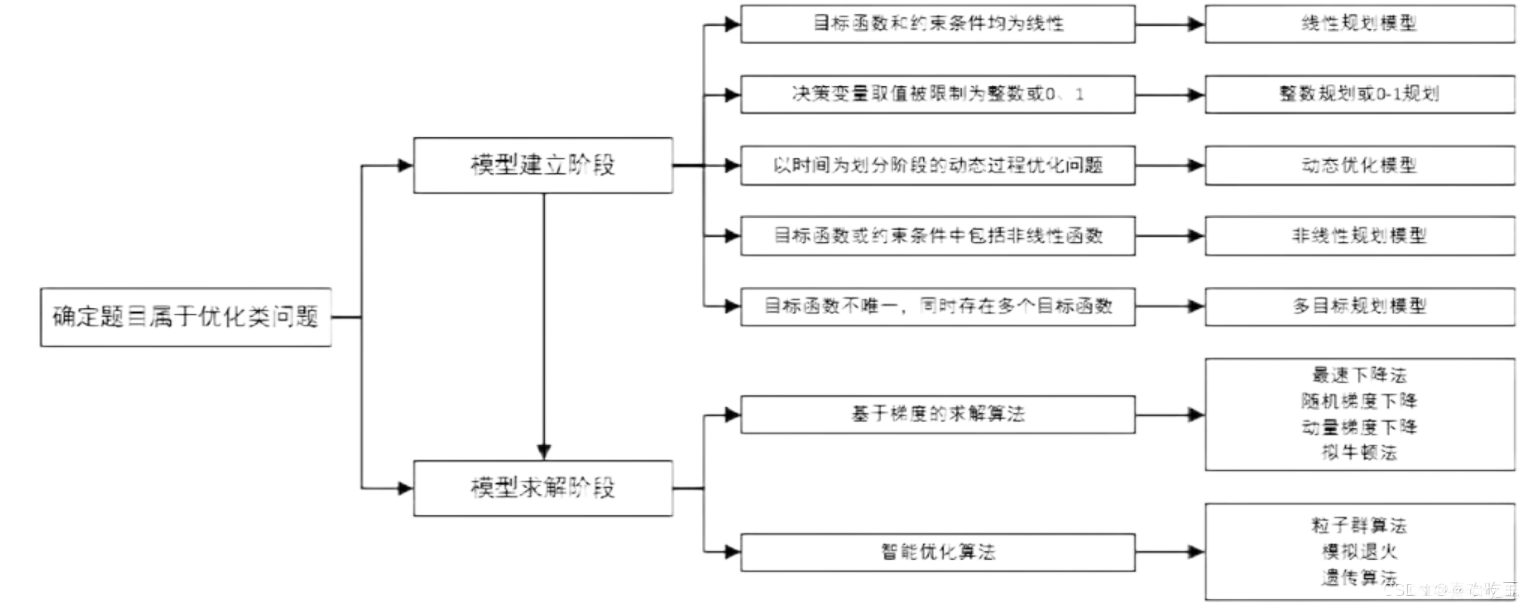
如何选择合适的优化方法

优化类问题中常用的数学模型和求解算法，其中包括线性规划、非线性规划、整数规划、多目标规划等。在模型求解中，对于凸优化模型，可以采用基于梯度的求解算法;对于非凸的优化模型，可以采用智能优化算法。

多目标优化问题

多目标优化问题，我们一般转化为单目标进行求解，主要有以下两种方法。

(1) 主要目标法

多目标优化问题中，多个目标之间可能不可兼得。即使是可以兼得的多个目标，可能也有主次。此时，我们可以选取我们最为关注的目标作为我们的主目标，而将其它次要目标转换为约束条件

(2) 线性加权法

多目标优化问题中，对多个分目标分别赋予一定的权重，合成一个总目标。通过总目标，兼顾各个目标。通过权重的大小体现我们对各个分目标的重视程度

关键，在转化到单目标的时候的合理性，可以用到层次分析法