今天给大家带来的是SIGIR 2022 一篇短文《Enhancing Hypergraph Neural Networks with Intent Disentanglement for Session-based Recommendation》，论文通过引入多意图解耦视角，分别从微观角度（超图构造和Intent Graph方法）与宏观角度（自监督意图分离）完成了会话推荐问题。论文由清华大学、美团共同完成，提出模型HIDE（Hypergraph Neural Networks with Intent DisEntanglement）。

论文地址：https://doi.org/10.1145/3477495.3531794

Introduction

作者在 intro 中回顾了会话推荐（Session-based Recommendation, SBR）的主要问题：

• 用户兴趣是动态的，复杂的
• Session 序列中除了能够体现user intent 的交互以外还包含 noises。

因此，作者提出了HIDE，主要思路就是将一个 item 对应到多个（$K$ 个）embedding，每个 embedding 对应到一个 intent，通过在微观角度、宏观角度分别完成对意图的解耦（Disentanglement），完成SBR预测。

具体来说，微观角度，主要通过构造超图，通过 n2e （节点到超边）和 e2n （超边到节点）完成节点的embedding更新。宏观角度，对 $K$ 个 intent 进行分离，主张多个 intent 应该对应到不同的 target item click，进行自监督训练，构成 auxiliary task。

下面进行详细介绍。

Preliminaries

问题形式化

V = { v 1 , v 2 , ⋯   , v m } \mathcal{V}=\{v_1, v_2, \cdots, v_m \} V={v1​,v2​,⋯,vm​} 表示物品集合，个数一共 $m$ 个。 一个匿名会话序列 $s$ 由若干通过时间顺序排列的交互物品组成，表示为：$s=\left[v_{s,1},v_{s,2},\cdots ,v_{s,n}\right]$，$v_{s,i}\in \mathcal{V}$ 表示交互物品，$n$ 表示会话长度。

问题形式化表示为：给定一个会话 session $s$ 的前 $n$ 个交互物品，需要预测第 $n+1$ 个物品（$v_{s,n+1}$）是什么。具体来说，完成一个排序问题，生成 $K$ 个候选物品，完成模型的 evaluation。

Hypergraph

超图（Hypergraph），其实就是点集。正常图通过点，以及两点之间的连线组成边构成。
超图就是在这个概念上更进一步，若干个点构成一个超边（Hyperedge），可以理解为超边中的节点两两连接。具体表示为：$\mathcal{G}=\left(\mathcal{V},\mathcal{E}\right)$，$\mathcal{V}$ 还是原来那个 $\mathcal{V}$， E = { e } \mathcal{E} = \left\{ e \right\} E={e} 表示超边集合，每条超边表示为 e = { v i 1 , v i 2 , ⋯   , v i k } e = \left\{ v_{i_{1}}, v_{i_{2}}, \cdots, v_{i_{k}} \right\} e={vi1​​,vi2​​,⋯,vik​​}，就是一个$\mathcal{V}$的子集，即$e\subseteq \mathcal{V}$。

Methodology

嵌入层 （Intent-Aware Embedding）

引入 Intent 概念，将 embedding 分为 $K$ 组，每组保持独立。
即，对于任意 $v\in \mathcal{V}$，其 intent-aware embedding表示为 ${\mathbf{h}}_{v_i}=\left({\mathbf{h}}_{v_i}^1,{\mathbf{h}}_{v_i}^2,\dots ,{\mathbf{h}}_{v_i}^K\right)$。每个物品具备$K$ 个 intent embedding ${\mathbf{h}}_{v_i}^k\in {\mathbb{R}}^{\frac{d}{K}}$，用于表示物品不同的 intent。
多个 intent 的中心概念化为 intent prototype， 通过平均池化表示为：${\mathbf{h}}_p^k=\mathrm{Mean}\left({\mathbf{h}}_{v_i}^k\mid v_i\in \mathcal{V}\right)$。

会话超图构建

如图1(a) 所示，通过 $3$ 种 超边构造超图，分别如下：

• Transition Hyperedges ${\mathcal{E}}_s^t$：每个 session 的会话图中所有 指向节点 $v$ 的节点 （incoming nodes）构成超边。
• Context Hyperedges ${\mathcal{E}}_s^c$：通过一个窗口大小为 $w$ 的滑动窗口，沿着会话序列方向移动，所有窗口内的物品构成超边。最大窗口为 $W$，取所有窗口截取到的超边并集作为上下文超边集合，即 ${\mathcal{E}}_s^c={\cup }_{w=1}^W{\mathcal{E}}_{s_w}^c$。
• Intent Hyperedges ${\mathcal{E}}_s^i$：对任意意图 k ∈ { 1 , 2 , ⋯   , K } k \in \left\{1, 2, \cdots, K\right\} k∈{1,2,⋯,K}，任意物品与intent prototype的相似性表示为 $S_{ki}=\cos \left({\mathbf{h}}_p^k,{\mathbf{h}}_{v_i}^k\right)$。Top-$\epsilon \cdot n$ 相似性分数的物品构成超边。其中，$\epsilon$ 为 比例系数， $n$ 为 session 长度。

上述所有超边的并集构成超边组合，即${\mathcal{E}}_s={\mathcal{E}}_s^t\cup {\mathcal{E}}_s^c\cup {\mathcal{E}}_s^i$。重合的边进行去除操作。

微观解耦

micro-disentanglement，实际上就是构造超图，完成 node->hyperedge->node 的embedding传播过程。具体而言：
1） Node to hyperedge (n2e) 可以表示为：

$${\mathbf{f}}_j^k={\mathbf{AGG}}_{n2e}\left({\alpha }_{jo}^k{\mathbf{h}}_{v_o}^k\mid v_o\in e_j\right)\text{\hspace{1em}(1)}$$
即通过GAT完成，GAT系数计算通过 softmax 进行归一化如下所示：

$${\alpha }_{jo}^k=\frac{\exp \left(\mathrm{LeakyReLU}\left({\mathbf{q}}_1^{k^{\top }}\left({\mathbf{h}}_{c_j}^k\odot {\mathbf{h}}_{v_{\mathbf{o}}}^k\right)\right)\right)}{{\sum }_{v_{o^{\prime }}\in e_j}\exp \left(\mathrm{LeakyReLU}\left({\mathbf{q}}_1^{k^{\top }}\left({\mathbf{h}}_{c_j}^k\odot {\mathbf{h}}_{v_{o^{\prime }}}^k\right)\right)\right)}\text{\hspace{1em}(2)}$$

2）Hyperedge to node (e2n) 可以表示为：

$${{\mathbf{h}}_{v_i}^k}^{\prime }={\mathbf{AGG}}_{e2n}\left({\beta }_{ij}^k{\mathbf{f}}_j^k\mid e_j\in {\mathcal{E}}_{s_{v_i}}\right)\text{\hspace{1em}(3)}$$
其中，GAT 网络注意力系数计算如下：

$${\beta }_{ij}^k=\frac{\exp \left(\mathrm{LeakyReLU}\left({\mathbf{q}}_2^{k^{\top }}\left({\mathbf{h}}_{q_{v_i}}^k\odot {\mathbf{f}}_j^k\right)\right)\right)}{{\sum }_{e_{j^{\prime }}\in {\mathcal{E}}_{s_{v_i}}}\exp \left(\mathrm{LeakyReLU}\left({\mathbf{q}}_2^{k^{\top }}\left({\mathbf{h}}_{q_{v_i}}^k\odot {\mathbf{f}}_{j^{\prime }}^k\right)\right)\right)}\text{\hspace{1em}(4)}$$

这里，${\mathbf{h}}_{q_{v_i}}^k={\mathbf{h}}_{v_i}^k+{\mathbf{s}}^k$，${\mathbf{s}}^k$ 表示当前 intent 下 session 中所有物品 embedding 的期望。

通过n2e, e2n，得到 refined embedding ${{\mathbf{h}}_{v_i}^k}^{\prime }$。

宏观解耦

Macro-disentanglement，即预测当前 intent 下的 target 目标，并计算损失：

$${\hat{\mathbf{y}}}_s^p=\mathrm{Softmax}\left(\mathrm{MLP}\left(\left\{{\mathbf{h}}_{v_i}^{k^{\prime }}\mid v_i\in {\mathcal{V}}_s\right\}\right)\right),\text{\hspace{1em}(5)}$$
这里，$\mathrm{MLP}\left(\cdot \right)$ 表示单层MLP网络，得到了 ${\hat{\mathbf{y}}}_s^p$ 表示 session $s$ 下对所有物品的预测分数，只对当前 intent 进行计算，得到当前 intent 的计算分数如下：

$${\mathcal{L}}_d^s=-\sum _{k=1}^K{1}_{p=k}\log \left({\hat{y}}_{sk}^p\right),\text{\hspace{1em}(6)}$$
这里 $1_{p=k}$ 表示 指示函数，只有在预测当前 intent 时赋值为 $1$。

预测层

如上所示，针对会话 $s=\left[v_{s,1},v_{s,2},\cdots ,v_{s,n}\right]$，任意物品 $v_{s_i}$ 具有intent-specific embedding chunks $\left({\mathbf{h}}_{v_{s_i}}^1{}^{\prime },{\mathbf{h}}_{v_{s_i}}^2{}^{\prime },\dots ,{{\mathbf{h}}_{v_{s_i}}^K}^{\prime }\right)$。

Inspired by GCE-GNN，通过将最后一个物品作为锚，计算注意力系数 ${\gamma }_i^k$ 对物品 embedding 进行整合，具体如下：

$$\begin{array}{rl}& {\mathbf{z}}_i^k=\tanh \left({\mathbf{W}}_1^k\left[{\mathbf{h}}_{v_{s_i}}^k{}^{\prime }\Vert {\mathbf{p}}_{n-i+1}\right]\right),{\mathbf{h}}_{s^{\ast }}^k={\mathbf{W}}_2^k\left[{\mathbf{h}}_{v_{s_i}}^k{}^{\prime }\Vert {\mathbf{h}}_{v_{s_n}}^k{}^{\prime }\right],\\ & {\gamma }_i^k={\mathrm{q}}^{k^{\top }}\sigma \left(\left({\mathbf{W}}_3^k\left[{\mathbf{h}}_{v_{s_i}}^k{}^{\prime }{}^{\prime }\odot {\mathbf{h}}_{s\ast }^k\right]\right)\Vert \left({\mathbf{W}}_4^k{\mathbf{h}}_{s\ast }^k\right)\Vert \left({\mathbf{W}}_5^k{\mathbf{z}}_i^k\right)+{\mathbf{b}}^k\right),\end{array}\text{\hspace{1em}(7)}$$
其中，${\mathbf{p}}_{n-i+1}$ 表示位置embedding，具体实现没说，应该是参考 GAT 的做法进行位置编码。${\mathbf{h}}_{v_{s_i}}^{\prime }$ 是物品 embedding。

${\mathbf{W}}_1^k,{\mathbf{W}}_2^k\in {\mathbb{R}}^{\frac{d}{K}\times \frac{2d}{K}}$，${{\mathbf{W}}_i^k|}_{i=3}^5\in {\mathbb{R}}^{\frac{d}{K}\times \frac{d}{K}}$，${\mathbf{b}}^k$，及 ${\mathbf{q}}^k\in {\mathbb{R}}^{\frac{3d}{K}}$ 都是 可训练权重参数。

从而得到 session 表示：
$${\mathbf{h}}_s^k=\sum _{i=1}^n{\gamma }_i^k\cdot {\mathbf{h}}_{v_{si}}^k{}^{\prime },\text{\hspace{1em}(8)}$$
对 $K$ 个 intent 进行加和，得到预测分数：
$$p_{si}=\sum _{k=1}^K{\mathbf{h}}_s^{k^{\top }}{\mathbf{h}}_{v_i}^k.\text{\hspace{1em}(9)}$$

模型训练

损失项通过 primary & auxiliary 方式进行，如下所示：
$${\mathcal{L}}_r^s=-\sum _{i=1}^m{y}_{si}\log \left({\hat{y}}_{si}\right)+\left(1-y_{si}\right)\log \left(1-{\hat{y}}_{si}\right),\text{\hspace{1em}(10)}$$

$${\mathcal{L}}^s={\mathcal{L}}_r^s+\lambda {\mathcal{L}}_d^s\text{\hspace{1em}(11)}$$

Experiments

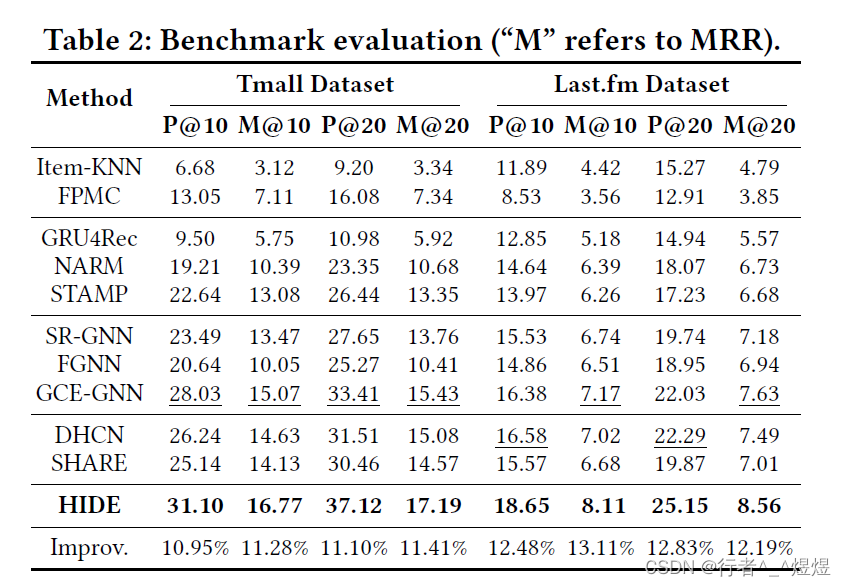
• 数据集：TMall 和 LastFM
• Metric：Precision@K、MRR@K
• 实验结果如下：

论文总结

文章整体较为完整，由于短文篇幅限制，一些内容语焉不详，例如超图在 $K$ 个意图下的划分，除此以外比较突出。