1 原理说明
原理部分网上其他文章[1][2]也已经说的比较明白了,这里不再赘述。
2 总体流程
参考论文作者开源的Matlab代码[3]和github上的C++代码[4]进行说明(不得不说还是Matlab代码更优雅)
论文方法总体分两部,第一部是在画面中找到所有的类棋盘格角点,第二步是角点的基础上构建出棋盘格形状。

3 模块说明
3.1 寻找角点
论文寻找角点的思想是用2x4个模板对输入图像进行逐像素匹配,得到类棋盘格角点,然后使用优化方法对角点进行亚像素优化得到最终角点;

寻找角点算法流程如下:
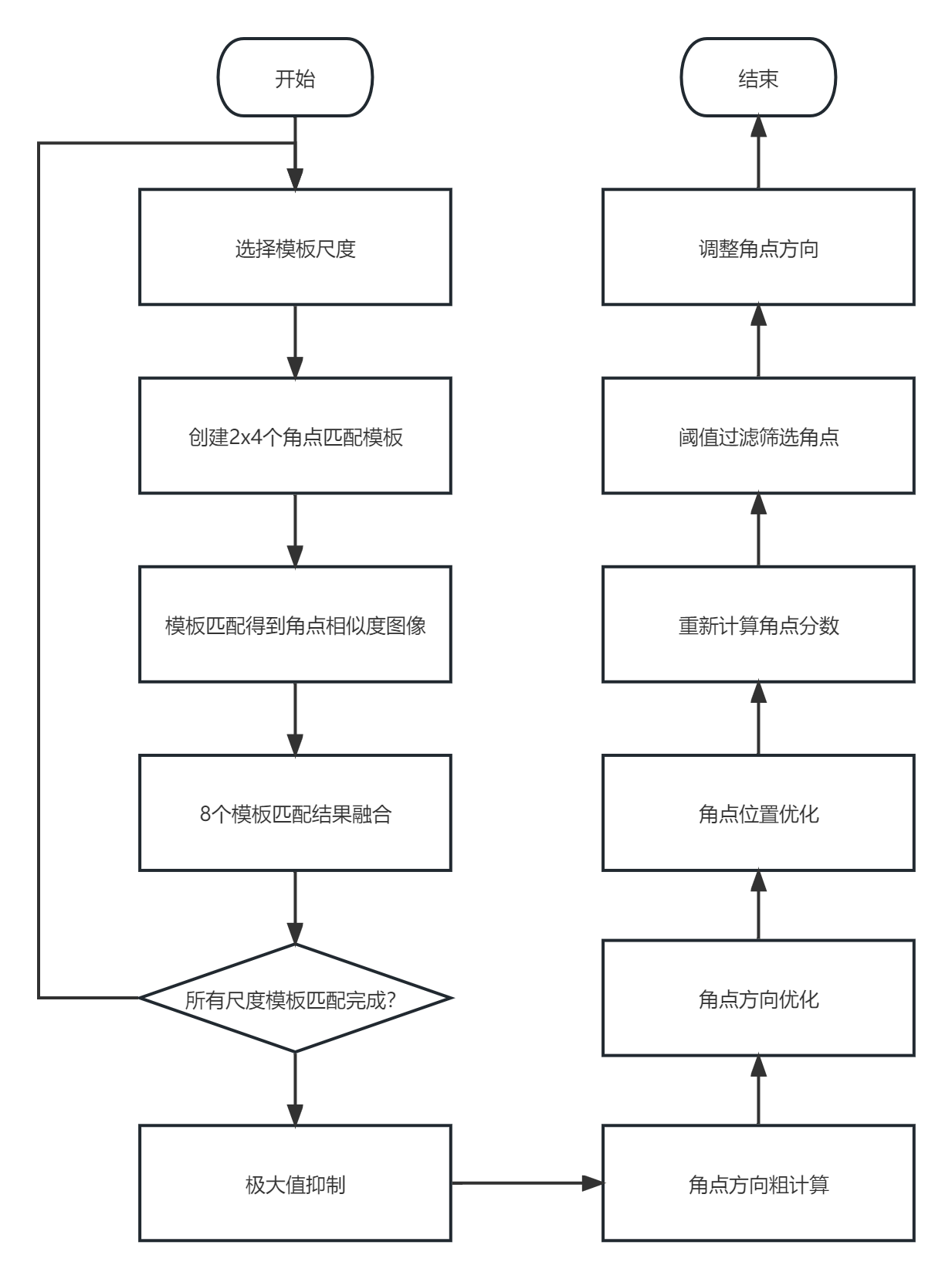
总体来说寻找角点的流程可分为4步:
- 模板匹配:包括选择尺度、模板创建、模板匹配、结果融合
- 非极大值抑制
- 角点优化:包括角点方向计算和优化、角点位置优化
- 分数计算和角点调整:包括分数计算、角点调整
3.1.1 模板匹配
论文中模板匹配使用了2x4个模板(见上述)对全图像进行匹配,为了适应不同尺度的棋盘格图像,论文创建了3种不同尺度的2x4个模板。
% 3 scales
radius(1) = 4;
radius(2) = 8;
radius(3) = 12;
% template properties
template_props = [
0 pi/2 radius(1); pi/4 -pi/4 radius(1); % 小尺度
0 pi/2 radius(2); pi/4 -pi/4 radius(2); % 中尺度
0 pi/2 radius(3); pi/4 -pi/4 radius(3)]; % 大尺度
disp('Filtering ...');
% filter image
img_corners = zeros(size(img,1),size(img,2));
for template_class=1:size(template_props,1)
% create correlation template
template = createCorrelationPatch(template_props(template_class,1),template_props(template_class,2),template_props(template_class,3));
% filter image according with current template
img_corners_a1 = conv2(img,template.a1,'same');
img_corners_a2 = conv2(img,template.a2,'same');
img_corners_b1 = conv2(img,template.b1,'same');
img_corners_b2 = conv2(img,template.b2,'same');
end在得到不同模板的结果后需要进行结果融合,论文给的公式是:
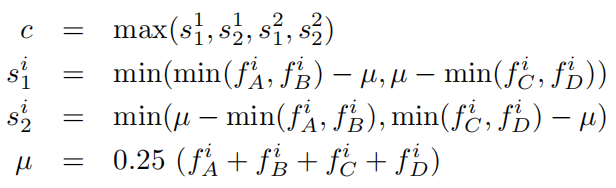
对应的实现是:
% compute mean
img_corners_mu = (img_corners_a1+img_corners_a2+img_corners_b1+img_corners_b2)/4;
% case 1: a=white, b=black
img_corners_a = min(img_corners_a1-img_corners_mu,img_corners_a2-img_corners_mu);
img_corners_b = min(img_corners_mu-img_corners_b1,img_corners_mu-img_corners_b2);
img_corners_1 = min(img_corners_a,img_corners_b);
% case 2: b=white, a=black
img_corners_a = min(img_corners_mu-img_corners_a1,img_corners_mu-img_corners_a2);
img_corners_b = min(img_corners_b1-img_corners_mu,img_corners_b2-img_corners_mu);
img_corners_2 = min(img_corners_a,img_corners_b);
% update corner map
img_corners = max(img_corners,img_corners_1);
img_corners = max(img_corners,img_corners_2);3.1.2 非极大值抑制
这个就不详细介绍了,反正就是非极大值抑制...
3.1.3 角点优化
论文中对于角点优化说的不咋详细,所以主要参考作者的开源代码。这一部分主要的步骤是:
- Sobel算子计算图像x,y方向梯度
- 根据图像梯度计算图像梯度方向和权重(强度)
- 根据图像附近区域像素梯度方向和权重,计算角点方向
- 对应论文中的梯度方向直方图统计过程
function [v1,v2] = edgeOrientations(img_angle,img_weight)
% init v1 and v2
v1 = [0 0];
v2 = [0 0];
% number of bins (histogram parameter)
bin_num = 32;
% convert images to vectors
vec_angle = img_angle(:);
vec_weight = img_weight(:);
% convert angles from normals to directions
vec_angle = vec_angle+pi/2;
vec_angle(vec_angle>pi) = vec_angle(vec_angle>pi)-pi;
% create histogram
angle_hist = zeros(1,bin_num);
for i=1:length(vec_angle)
bin = max(min(floor(vec_angle(i)/(pi/bin_num)),bin_num-1),0)+1;
angle_hist(bin) = angle_hist(bin)+vec_weight(i);
end
% find modes of smoothed histogram
[modes,angle_hist_smoothed] = findModesMeanShift(angle_hist,1);
% if only one or no mode => return invalid corner
if size(modes,1)<=1
return;
end
% compute orientation at modes
modes(:,3) = (modes(:,1)-1)*pi/bin_num;
% extract 2 strongest modes and sort by angle
modes = modes(1:2,:);
[foo idx] = sort(modes(:,3),1,'ascend');
modes = modes(idx,:);
% compute angle between modes
delta_angle = min(modes(2,3)-modes(1,3),modes(1,3)+pi-modes(2,3));
% if angle too small => return invalid corner
if delta_angle<=0.3
return;
end
% set statistics: orientations
v1 = [cos(modes(1,3)) sin(modes(1,3))];
v2 = [cos(modes(2,3)) sin(modes(2,3))];- 角点方向优化
- 步骤3中计算角点方向比较粗糙,这里对方向进行优化处理
- 优化方法对应论文公式(4),主要是计算角点附件有效点的梯度累加矩阵的最小特征值对应的特征向量(有点拗口:D)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% corner orientation refinement %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A1 = zeros(2,2);
A2 = zeros(2,2);
for u=max(cu-r,1):min(cu+r,width)
for v=max(cv-r,1):min(cv+r,height)
% pixel orientation vector
o = [img_du(v,u) img_dv(v,u)];
if norm(o)<0.1
continue;
end
o = o/norm(o);
% robust refinement of orientation 1
if abs(o*v1')<0.25 % inlier?
A1(1,:) = A1(1,:) + img_du(v,u) * [img_du(v,u) img_dv(v,u)];
A1(2,:) = A1(2,:) + img_dv(v,u) * [img_du(v,u) img_dv(v,u)];
end
% robust refinement of orientation 2
if abs(o*v2')<0.25 % inlier?
A2(1,:) = A2(1,:) + img_du(v,u) * [img_du(v,u) img_dv(v,u)];
A2(2,:) = A2(2,:) + img_dv(v,u) * [img_du(v,u) img_dv(v,u)];
end
end
end
% set new corner orientation
[v1,foo1] = eig(A1); v1 = v1(:,1)'; corners.v1(i,:) = v1;
[v2,foo2] = eig(A2); v2 = v2(:,1)'; corners.v2(i,:) = v2;- 角点位置优化
- 优化方法对应论文公式(2),求解方法对应论文公式(3)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% corner location refinement %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
G = zeros(2,2);
b = zeros(2,1);
for u=max(cu-r,1):min(cu+r,width)
for v=max(cv-r,1):min(cv+r,height)
% pixel orientation vector
o = [img_du(v,u) img_dv(v,u)];
if norm(o)<0.1
continue;
end
o = o/norm(o);
% robust subpixel corner estimation
if u~=cu || v~=cv % do not consider center pixel
% compute rel. position of pixel and distance to vectors
w = [u v]-[cu cv];
d1 = norm(w-w*v1'*v1);
d2 = norm(w-w*v2'*v2);
% if pixel corresponds with either of the vectors / directions
if d1<3 && abs(o*v1')<0.25 || d2<3 && abs(o*v2')<0.25
du = img_du(v,u);
dv = img_dv(v,u);
H = [du dv]'*[du dv];
G = G + H;
b = b + H*[u v]';
end
end
end
end
% set new corner location if G has full rank
if rank(G)==2
corner_pos_old = corners.p(i,:);
corner_pos_new = (G\b)';
corners.p(i,:) = corner_pos_new;
% set corner to invalid, if position update is very large
if norm(corner_pos_new-corner_pos_old)>=4
corners.v1(i,:) = [0 0];
corners.v2(i,:) = [0 0];
end
% otherwise: set corner to invalid
else
corners.v1(i,:) = [0 0];
corners.v2(i,:) = [0 0];
end3.1.4 分数计算和角点调整
- 分数计算
分数计算是用来计算每个角点的得分,然后与用户设置的阈值进行比较,如果超过阈值则为合格角点。这里论文说的和代码里面的有点对不上感觉,论文说方法的是求角点附近图像的二阶导,然后和一个模板做normalized cross-correlation;但是代码里面实现的方式是:
- 计算论文中Figure 2.e中的模板T
% center
c = ones(1,2)*(size(img_weight,1)+1)/2;
% compute gradient filter kernel (bandwith = 3 px)
img_filter = -1*ones(size(img_weight,1),size(img_weight,2));
for x=1:size(img_weight,2)
for y=1:size(img_weight,1)
p1 = [x y]-c;
p2 = p1*v1'*v1;
p3 = p1*v2'*v2;
if norm(p1-p2)<=1.5 || norm(p1-p3)<=1.5
img_filter(y,x) = +1;
end
end
end- 将模板T与之前得到的图像梯度权重分别做归一化,然后做相关,得到相关系数score_gradient
% convert into vectors
vec_weight = img_weight(:);
vec_filter = img_filter(:);
% normalize
vec_weight = (vec_weight-mean(vec_weight))/std(vec_weight);
vec_filter = (vec_filter-mean(vec_filter))/std(vec_filter);
% compute gradient score
score_gradient = max(sum(vec_weight.*vec_filter)/(length(vec_weight)-1),0);- 按角点的2个主方向生成4个模板
- 计算模板匹配值score_intensity(过程与3.1.1的模板匹配一样)
% create intensity filter kernel
template = createCorrelationPatch(atan2(v1(2),v1(1)),atan2(v2(2),v2(1)),c(1)-1);
% checkerboard responses
a1 = sum(template.a1(:).*img(:));
a2 = sum(template.a2(:).*img(:));
b1 = sum(template.b1(:).*img(:));
b2 = sum(template.b2(:).*img(:));
% mean
mu = (a1+a2+b1+b2)/4;
% case 1: a=white, b=black
score_a = min(a1-mu,a2-mu);
score_b = min(mu-b1,mu-b2);
score_1 = min(score_a,score_b);
% case 2: b=white, a=black
score_a = min(mu-a1,mu-a2);
score_b = min(b1-mu,b2-mu);
score_2 = min(score_a,score_b);
% intensity score: max. of the 2 cases
score_intensity = max(max(score_1,score_2),0);- 计算score = score_intensity * score_gradient
- 改变模板尺度(与 3.1.1一样),重复步骤1~5,计算所有尺度中的分数最大值
不知道论文和代码中的方法是否等价,留以后考证。
- 角度调整
这部分主要是对计算角点的主方向做一个调整,以减少后面多图像匹配(我们用不到)过程中的歧义性
% make v1(:,1)+v1(:,2) positive (=> comparable to c++ code)
idx = corners.v1(:,1)+corners.v1(:,2)<0;
corners.v1(idx,:) = -corners.v1(idx,:);
% make all coordinate systems right-handed (reduces matching ambiguities from 8 to 4)
corners_n1 = [corners.v1(:,2) -corners.v1(:,1)];
flip = -sign(corners_n1(:,1).*corners.v2(:,1)+corners_n1(:,2).*corners.v2(:,2));
corners.v2 = corners.v2.*(flip*ones(1,2));3.2 构建棋盘格
论文提出的棋盘格构建是基于生长的方法,所以首先要选定几个点作为初始棋盘格,然后在初始棋盘格的基础上向外生长,在生长的过程中需要对多种可能的生长方式进行判断,判断新生长出来的棋盘格是不是最优,最终得到最优的棋盘格结构。

通过上述步骤,可以得到多个棋盘格结构,如果这些棋盘格结构中有重叠的话,则需要做一个去重处理。
对于判断生长和去重过程中的哪个棋盘格结构更优,论文给出了一种棋盘格能量计算方法,参考论文公式(6)。
所以整体棋盘格构建流程如下:
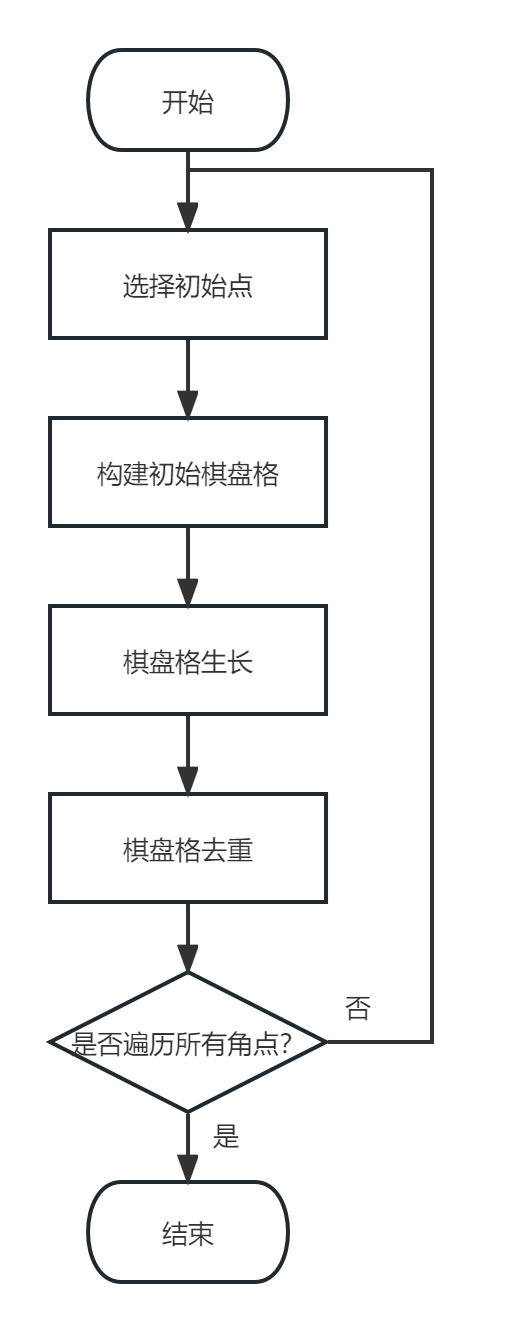
3.2.1 选择初始点
没什么讲究,所有点都拿来试一试...
3.2.2 构建初始棋盘格
构建初始棋盘格是将选择的初始点扩展成3x3共9个点,组成一个小小的初始棋盘格。方法是从初始点开始,往2个主方向和2个主方向的反方向(一共4个方向)各找一个距离最近的点,这样就有了5个点,然后再从上下两个点以同样的方法往左右扩展,最终形成3x3棋盘格。
% return if not enough corners
if size(corners.p,1)<9
chessboard = [];
return;
end
% init chessboard hypothesis
chessboard = zeros(3,3);
% extract feature index and orientation (central element)
v1 = corners.v1(idx,:);
v2 = corners.v2(idx,:);
chessboard(2,2) = idx;
% find left/right/top/bottom neighbors
[chessboard(2,3),dist1(1)] = directionalNeighbor(idx,+v1,chessboard,corners);
[chessboard(2,1),dist1(2)] = directionalNeighbor(idx,-v1,chessboard,corners);
[chessboard(3,2),dist2(1)] = directionalNeighbor(idx,+v2,chessboard,corners);
[chessboard(1,2),dist2(2)] = directionalNeighbor(idx,-v2,chessboard,corners);
% find top-left/top-right/bottom-left/bottom-right neighbors
[chessboard(1,1),dist2(3)] = directionalNeighbor(chessboard(2,1),-v2,chessboard,corners);
[chessboard(3,1),dist2(4)] = directionalNeighbor(chessboard(2,1),+v2,chessboard,corners);
[chessboard(1,3),dist2(5)] = directionalNeighbor(chessboard(2,3),-v2,chessboard,corners);
[chessboard(3,3),dist2(6)] = directionalNeighbor(chessboard(2,3),+v2,chessboard,corners);
% initialization must be homogenously distributed
if any(isinf(dist1)) || any(isinf(dist2)) || ...
std(dist1)/mean(dist1)>0.3 || std(dist2)/mean(dist2)>0.3
chessboard = [];
return;
end可以看到,在通过directionalNeighbor扩展了之后,还对扩展出去的距离做了一个判断,避免产生太过离谱的初始棋盘格。
directionalNeighbor的具体实现如下,其中dist_point+5*dist_edge作为距离这一个有点迷,可能是想兼顾考虑径向和切向距离,但是不知道数学原理是什么(虽然效果确实不错)
function [neighbor_idx,min_dist] = directionalNeighbor(idx,v,chessboard,corners)
% list of neighboring elements, which are currently not in use
unused = 1:size(corners.p,1);
used = chessboard(chessboard~=0);
unused(used) = [];
% direction and distance to unused corners
dir = corners.p(unused,:) - ones(length(unused),1)*corners.p(idx,:);
dist = (dir(:,1)*v(1)+dir(:,2)*v(2));
% distances
dist_edge = dir-dist*v;
dist_edge = sqrt(dist_edge(:,1).^2+dist_edge(:,2).^2);
dist_point = dist;
dist_point(dist_point<0) = inf;
% find best neighbor
[min_dist,min_idx] = min(dist_point+5*dist_edge);
neighbor_idx = unused(min_idx);3.2.3 棋盘格生长
这个流程没啥好说的,确定了初始棋盘格之后,就不断往4个方向生长,然后选一个能量最低的作为最优解,作为新的初始棋盘格。
% try growing chessboard
while 1
% compute current energy
energy = chessboardEnergy(chessboard,corners);
% compute proposals and energies
for j=1:4
proposal{j} = growChessboard(chessboard,corners,j);
p_energy(j) = chessboardEnergy(proposal{j},corners);
end
% find best proposal
[min_val,min_idx] = min(p_energy);
% accept best proposal, if energy is reduced
if p_energy(min_idx)<energy
chessboard = proposal{min_idx};
% otherwise exit loop
else
break;
end
end3.2.4 棋盘格去重
当棋盘格中包含的任意一个角点在已存在的棋盘格中也存在了,则认为存在棋盘格重复。去重采用的方法是看看当前棋盘格的和已存在的棋盘格哪个更优(哪个能量更低),如果当前棋盘格能量更低,则替换掉原来的棋盘格。
% if chessboard has low energy (corresponding to high quality)
if chessboardEnergy(chessboard,corners)<-10
% check if new chessboard proposal overlaps with existing chessboards
overlap = zeros(length(chessboards),2);
for j=1:length(chessboards)
for k=1:length(chessboards{j}(:))
if any(chessboards{j}(k)==chessboard(:))
overlap(j,1) = 1;
overlap(j,2) = chessboardEnergy(chessboards{j},corners);
break;
end
end
end
% add chessboard (and replace overlapping if neccessary)
if ~any(overlap(:,1))
chessboards{end+1} = chessboard;
else
idx = find(overlap(:,1)==1);
if ~any(overlap(idx,2)<=chessboardEnergy(chessboard,corners))
chessboards(idx) = [];
chessboards{end+1} = chessboard;
end
end
end4 参考资料
[1] Geiger, A., Moosmann, F., Car, Ö. and Schuster, B., 2012, May. Automatic camera and range sensor calibration using a single shot. In 2012 IEEE international conference on robotics and automation (pp. 3936-3943). IEEE.
[2] 基于生长的棋盘格角点检测方法--(1)原理介绍_findchessboardcornerssb原理介绍_计算机视觉life的博客-CSDN博客
[3] Andreas Geiger (cvlibs.net)
[4] onlyliucat/Multi-chessboard-Corner-extraction-detection-: chess board corner extraction and chess board recovery "Automatic Camera and Range Sensor Calibration using a single Shot" (github.com)


![[架构之路-221]:鸿蒙系统和安卓系统的比较:微内核VS宏内核, 分布式VS单体式](https://img-blog.csdnimg.cn/9690df1791a041a8b848d3080ca01510.png)