89. 格雷编码

news2025/1/11 11:50:48

解题思路：

解法一：找规律，2-4位格雷码的码表如下图所示（二进制表示）：

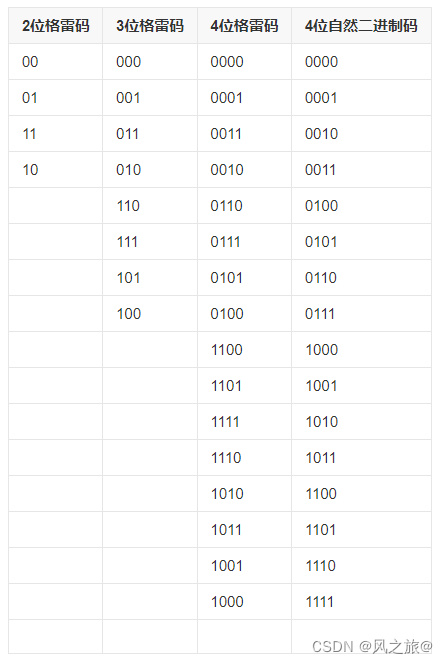
可以发现，n位格雷码序列可以由n-1位格雷码序列得到，满足递归规则，具体构造规则如下：

1位格雷码有两个码字：0，1。n=1时，递归终止。
n位格雷码序列中的前2^n个码字等于n-1位格雷码的码字，按顺序书写，加前缀0
n位格雷码序列中的后2^n个码字等于n-1位格雷码的码字，按逆序书写，加前缀1
即：n位格雷码的序列集合 = n-1位格雷码集合(顺序)加前缀0 + n-1位格雷码集合(逆序)加前缀1

通过上述递归求解出n位格雷码中每一个码字的二进制序列，然后将该二进制序列转为十进制，即所求

AC代码：

class Solution {
    public static List<Integer> grayCode(int n) {
        List<String> result = binGrayCode(n);
        List<Integer> ans = new ArrayList<>();
        for (String str : result) {
            int num = Integer.parseInt(str, 2);
            ans.add(num);
        }
        return ans;
    }

    public static List<String> binGrayCode(int n){
        ArrayList<String> result = new ArrayList<>();
        if (n==1){
            result.add("0");
            result.add("1");
            return result;
        }
        List<String> ans = binGrayCode(n - 1);
        for (String an : ans) {
            result.add("0" + an);
        }
        for (int i = ans.size()-1; i >=0; i--) {
            result.add("1"+ans.get(i));
        }

        return result;
    }
}

方法二：公式法：

第i个格雷码等于：

$g_{i}=i\bigoplus \left \lfloor \frac{i}{2}\right \rfloor$

即 i 与 i/2向下取整的异或值

AC代码：

class Solution {
    public static List<Integer> grayCode(int n) {
        ArrayList<Integer> result = new ArrayList<>();
        for (int i = 0; i < 1 << n; i++) {
            result.add(i ^ (i >> 1));
        }
        return result;
    }
}