机器学习西瓜书+南瓜书吃瓜教程学习笔记第五章神经网络

news2025/1/11 11:34:34

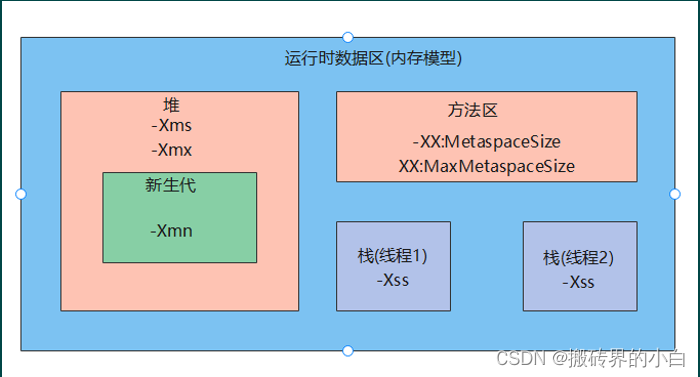
来自吃瓜教程】《机器学习公式详解》（南瓜书）与西瓜书公式推导直播合集第五章神经网络
和周志华老师的机器学习西瓜书
以下是我的学习笔记：
神经网络：
神经网络是由具有适应性的简单单元组成的广泛并行互联的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
标准神经网络算法工作流程：
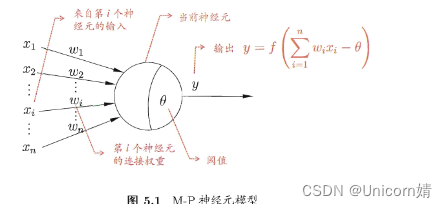
在这里插入图片描述

1、M-P神经元

（一个用来模拟生物行为的数学模型）：接收n个输入(通常是来自其他神经元)，并给各个输入赋予权重计算加权和，然后和自身特有的阈值进行比较（作减法），最后经过激活函数（模拟“抑制（小于0）”和“激活（大于0）”）处理得到输出（通常是给下一个神经元（当作输入））
$y=f\left( \sum ^{n}_{i=1}w_{i}x_{i}-\theta \right) =f\left( w^{T}x+b\right)$ （向量化，抽象为线性模型形式）
单个M-P神经元：感知机（sign作激活函数）、对数几率回归（sigmoid作激活函数）
多个M-P神经元：神经网络
在这里插入图片描述

从数学角度
在这里插入图片描述

线性可分的数据集是指存在一个超平面（在二维空间中即为一条直线，三维空间中为一个平面，
高维空间中为一个超平面），能够将不同类别的数据完全分开的数据集。
具体而言，对于一个二分类问题，如果存在一个超平面能够将所有正类样本和负类样本完全分开
，且没有任何样本点处于超平面上或超平面两侧靠得非常近，那么这个数据集就被称为线性可分的。

从几何角度来说，给定一个线性可分的数据集T，感知机的学习目标是球的能对数据集T中的正负样本完全正确划分的超平面，其中 $w^{T}x+b=0$ 即为超平面方程。（令方程=0把 $-\theta$ 看作-b）
n维空间的超平面的性质：

超平面方程不唯一
法向量w垂直与超平面
法向量w和位移项b确定一个唯一超平面
法向量w指向的那一半空间为正空间（正空间上的点是大于0的），另一半为负空间（负空间上的点是小于0的），而在这个超平面上的点是等于0的。

2、感知机学习策略

随机初始化w,b，将全体训练样本代入模型找出误分类样本。对于任意一个误分类样本来说，当 $W^{T}x-\theta$ 大于等于0时，模型输出值为y=1,样本真实标记为y=0；反之，当 $W^{T}x-\theta$ 小于0时，模型输出值为y=0，样本真实标记值记为y=1，所以可以得出：
$\left( \widehat{y}-y\right) \left( w^{T}x-\theta \right) \geq 0$ 这个式子恒成立
所以，当给出数据集T，我们可以定义其损失函数为
$L\left( W,\theta \right) =\sum _{x\in M}\left( \widehat{y}-y\right) \left( w^{T}-\theta \right)$
显然，此损失函数是非负的。如果没有误分类点，损失函数值是0.而且，误分类点越少，误分类点离超平面越近，损失函数值就越小。
在这里插入图片描述

3、感知机学习算法

描述：当误分类样本集合M固定时，那么可以求得损失函数L(w)地梯度为
$\Delta _{w}L\left( w\right) =\sum _{x_{i}\in M}\left( \widehat{y_{i}}-y_{i}\right) x_{i}$
感知机的学习算法具体采用的是随机梯度下降法，也就是极小化过程中不是一次使M中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。
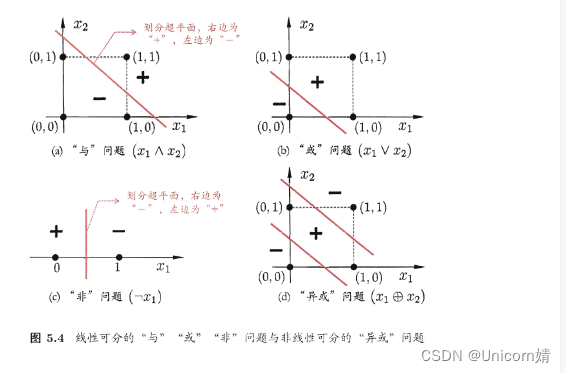
在这里插入图片描述

感知机属于单个神经元分类能力有限，只能分类线性可分的数据集，
如果要解决非线性可分的问题，需考虑使用多层功能神经元。
且有理论证明（通用近似定理）：只需一个包含足够多神经元的隐层，多层前馈网络（最经典的神经网络之一）就能以任意精度逼近任意复杂度的连续函数（自己需要构造特征，输入进神经网络会帮忙构造出一些特征，可能恰好就构造出了符合的特征,自己对数据进行加工）。因此，神经网络既能做回归，也能做分类，而且不需要复杂的特征工程。

特征工程（Feature Engineering）是指通过数据预处理和特征处理等手段，将原始数据转换为更有意义、更易于被机器学习算法使用的特征表示的过程。特征在机器学习中起着至关重要的作用，合适的特征能够提高模型的准确性和泛化能力，而不合适的特征则会降低模型的性能。
特征工程包括以下几个方面：
数据清洗：对数据进行去重、缺失值处理、异常值处理等操作，确保数据质量和完整性。
特征选择：根据领域知识、统计分析、特征重要性等方法，选取对目标变量具有较强预测能力的特征。
避免冗余特征和无用特征对模型性能的影响。
特征提取：通过特定的方法将原始数据转化为新的特征表示。例如，数值型特征可以进行离散化、分箱、
标准化等预处理；文本数据可以进行词袋模型、TF-IDF等特征提取方式。
特征构建：人工构造新的特征，使得特征表现出更好的分类或回归性质。该过程需要一定的领域知识
和创造性思维。
特征组合：将不同的特征进行组合，形成新的复合特征，提高模型的表达能力和泛化性能。
例如，对时间和地理位置进行组合，可以得到更具有区分度的特征。

理想很丰满，现实很骨感，神经网络还存在一些问题等待解决：
如面对一个具体的场景，神经网络该做多深，多宽？神经网络的结构该如何设计最合理？神经网络的输出结果该如何解释？

4、多层前馈网络

每层神经元与下一层神经元全互联，神经元之间不存在同层连接，也不存在跨层连接（隐层阈值 $y_{h}$ ，输出层阈值 $\theta _{j}$ ）
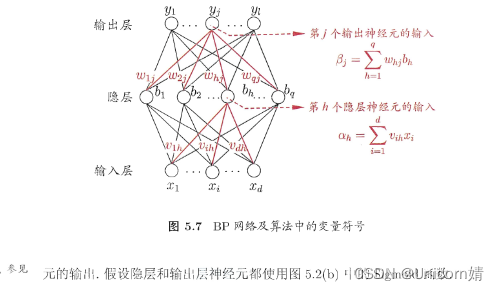
在这里插入图片描述
将神经网络（记为NN）看作一个特征加工函数
$x\in R^{d}\rightarrow NN\left( x\right) \rightarrow y=x^{\ast }\in R^{1}$
（单输出）回归：后面接一个 $R^{1}\rightarrow R$ 的神经元。例如：没有激活函数的神经元
$y=w^{T}x^{\ast }+b$
分类：后面接一个 $R^{1}\rightarrow \left[ 0,1\right]$ 的神经元，例如：激活函数为Sigmoid函数的神经元
$y=\dfrac{1}{1+e^{-\left( w^{T}x^{\ast }+b\right) }}$
在模型训练过程中，神经网络（NN）自动学习提取有用的特征，因此，机器学习向“全自动数据分析”又前进了一步。
但由于其强大的表示能力，BP神经网络经常遭遇过拟合，其训练误差持续降低，但测试误差却可能上升。由两种策略常用来缓解BP网络的过拟合，第一种策略是“早停”，第二种策略是“正则化”。回归任务损失函数可以采用均方误差，分类任务则用交叉熵。
误差逆传播算法（BP算法）：基于随机梯度下降的参数更新算法。
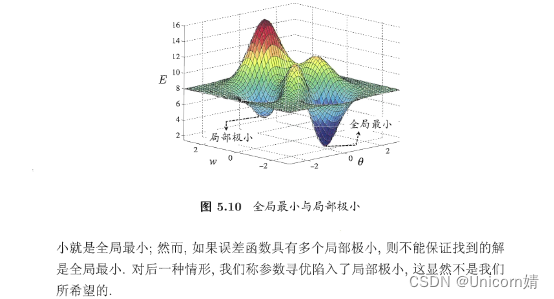
在这里插入图片描述
其中只需推导出E这个损失函数关于参数的一阶偏导数（梯度）即可（链式求导）。值得一提的是，由于NN(x)通常是极其复杂的非凸函数，不具备像凸函数这种良好的数学性质，因此随机梯度下降不能保证一定能走到全局最小值点，更多情况下走到的都是局部极小值点。
在这里插入图片描述