机器人学中有些问题是二值问题,对于这种二值问题的概率评估问题可以用二值贝叶斯滤波器binary Bayes filter来解决的。比如机器人前方有一个门,机器人想判断这个门是开是关。这个二值状态是固定的,并不会随着测量数据变量的改变而改变。就像门一样,不是开就是关。
现在我利用二值贝叶斯滤波来在跟踪阶段判断4d毫米波聚类后目标的动态和静态属性
当状态静止时。置信度仅是测量的函数:
b e l t ( x ) = p ( x ∣ z 1 : t , u 1 : t ) = p ( x ∣ z 1 : t ) (1) bel_t(x) = p(x|z_{1:t},u_{1:t}) = p(x|z_{1:t}) \tag 1 belt(x)=p(x∣z1:t,u1:t)=p(x∣z1:t)(1)
这里有两个状态,用 x x x和 ¬ x \neg x ¬x表示,具体来说: b e l t ( ¬ x ) = 1 − b e l t ( x ) bel_t(\neg x)= 1-bel_t(x) belt(¬x)=1−belt(x),状态 x x x不随时间变化。
置信度通常是以概率比的对数(log odds ratio)的形式实现的。 状态x的概率(odds)被定义此事件的概率除以该事件不发生的概率:
p
(
x
)
p
(
¬
x
)
=
p
(
x
)
1
−
p
(
x
)
(2)
\frac{p(x)}{p(\neg x)} = \frac{p(x)}{1-p(x)} \tag 2
p(¬x)p(x)=1−p(x)p(x)(2)
概率对数是这个表达式的对数:
l ( x ) : = p ( x ) 1 − p ( x ) (3) l(x): = \frac{p(x)}{1-p(x)} \tag 3 l(x):=1−p(x)p(x)(3)
概率对数假设值为 − ∞ ∼ ∞ - \infty \sim \infty −∞∼∞,避免了概率接近0或1引起的截断问题
事实上,任何对测量做出反应的变量的递增和递减都可以解释为贝叶斯滤波的概率对数形式。该二值贝叶斯滤波利用一个反向测量模型 p ( x ∣ z t ) p(x|z_t) p(x∣zt)代替熟悉的前向测量模型 p ( z t ∣ x ) p(z_t|x) p(zt∣x)。反向测量模型将关于(二值)状态变量的一个分布指定为测量 z t z_t zt的一个函数。
l t = l t − 1 + l o g p ( x ∣ z t ) 1 − p ( x ∣ z t ) − l o g p ( x ) 1 − p ( x ) (4) l_t = l_{t-1} + log \frac{p(x|z_t)}{1-p(x|z_t)} - log \frac{p(x)}{1-p(x)} \tag 4 lt=lt−1+log1−p(x∣zt)p(x∣zt)−log1−p(x)p(x)(4)
l t l_t lt是状态变量的后验置信度的概率对数,该二值状态变量不随时间变化
根据式(3)概率对数的定义证明,置信度
b
e
l
t
(
x
)
bel_t(x)
belt(x)可以根据概率比对数
l
t
l_t
lt通过下面的方式来求得:
b
e
l
t
(
x
)
=
1
−
1
1
+
e
x
p
{
l
t
}
bel_t(x) = 1- \frac{1}{1+exp\{l_t\}}
belt(x)=1−1+exp{lt}1
下面证明二值贝叶斯滤波算法的正确性:


在动态和静态属性更新中,
p
(
x
∣
z
t
)
p(x|z_t)
p(x∣zt)计算为速度大于给定值
v
d
v_d
vd的点数与目标点云中的点总数的比值。
t=0: 机器人对外界环境一无所知,p(x=静态)= p(x=动态)= 0.5
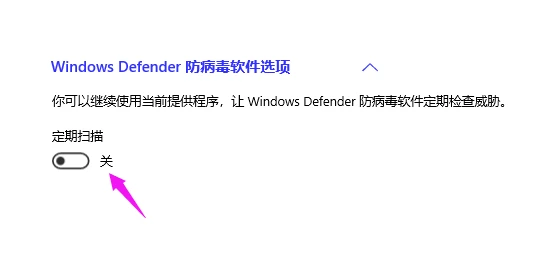
今天写代码验证效果!!!
参考:
- Thrun, S. Probabilistic Robotics. Commun. ACM 2002, 45, 52–57
- Tracking of Multiple Static and Dynamic Targets for 4D Automotive Millimeter-Wave Radar Point Cloud in Urban Environments. Remote. Sens. 15(11): 2923 (2023)