问题概述

 一家钢琴专卖店，根据以往的销售经验，平均每周只能售出一架钢琴，现在经理指定的存贮策略是，每周末检查库存存量，仅当库存量为零时，才订购3架供下周销售；否则就不订购。试估计这种策略下失去销售机会的可能性有多大，以及每周的平均销售量是多少。

【问题分析】 

1. 在商品销售中，顾客到大往往是独立的。在服务系统里，认为商品需求量近似服从泊松分布，其参数可由均值为每周销售1架钢琴得到，由此可以计算不同需求量的分布率。
2. 周末的库存可能是0,1,2,3这3种状态，每周不同的需求将导致周初的库存状态的变化，于是可以用马尔可夫链来描述这个过程。
3. 当需求超过库存时就会失去销售机会，可以计算这种情况发生的概率。在动态过程种这个概率每周不同，每周的销售量也不同。通常采用的办法时在时间充分长久后，按稳态情况进行计算。

【模型假设】

1. 钢琴周需求量服从参数为1的泊松分布
2. 存贮策略是：当周末库存量为0时，订购3架，周初到；否则，不订购
3. 以每周初的库存量为状态变量，状态转移无后效性
4. 在稳态情况下计算本案存贮策略失去销售的机会概率和周平均销售量

 【模型建立】

1、钢琴周需求量的分布规律

设Dn为第n周钢琴的需求量，由假设Dn服从P(1)，即

2、状态转移规律 

  设第n周初的库存量为Sn，则Sn∈{1,2,3}是这个系统的状态变量，有假设（2），状态转移规律为

 

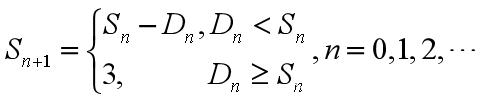
3、状态转移矩阵 

设状态转移矩阵为P=(pij)3×3,即 

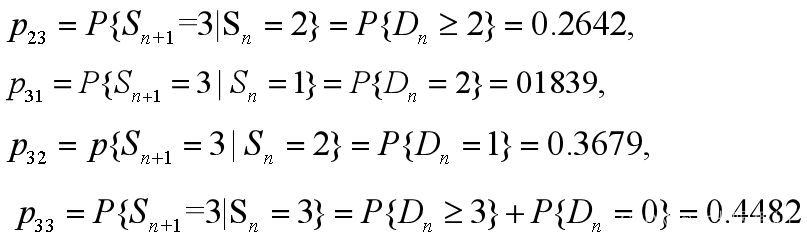 即，转移矩阵为

设ai(n)=P{Sn=i}为状态概率，i=1,2,3，根据无后效性，设 a(n)=[a1(n),a2(n),a3(n)],根据无后效性，得

4、稳态概率

p=[0.3679 0 0.6321;0.3679 0.3679 0.2642;0.1839 0.3679 0.4482];
[u,d]=eig(p');
w=u(:,1);w=w/sum(w)
w =
    0.2847
    0.2632
    0.4521

则稳态概率为w=[0.2847 0.2632 0.4521]

5、计算该存贮策略下周损失概率

当周需求量Dn大于周初存贮量Sn时，就存在销售损失。所以损失概率为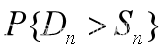

按照全概率公式有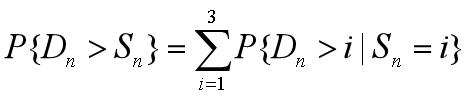 

根据假设4，这里P{Sn=i}=wi,i=1,2,3。计算结果为

p=[0.3679 0 0.6321;0.3679 0.3679 0.2642;0.1839 0.3679 0.4482];
[u,d]=eig(p');
w=u(:,1);w=w/sum(w);
q1=1-exp(-1)-exp(-1);
q2=1-exp(-1)-exp(-1)-exp(-1)/2;
q3=1-exp(-1)-exp(-1)-exp(-1)/2-exp(-1)/6;
q=[q1,q2,q3];
Loss=q*w
Loss =
    0.1049

 6、第n周的平均销售量E(Rn)

 第n周的销售量Rn是一个随机变量，由库存和需求两共同决定，Rn的取值情况如表5.

表5 第n周销售量取值

Sn\Rn\Dn	0	1	2	3	>=4
1	0	1	1	1	1
2	0	1	2	2	2
3	0	1	2	3	3

其中P{Sn=i}的概率用稳态概率来计算。根据二维离散随机变量的均值的定义，有 

p=[0.3679 0 0.6321;0.3679 0.3679 0.2642;0.1839 0.3679 0.4482];
[u,d]=eig(p');
w=u(:,1);w=w/sum(w);
ER=exp(-1)+w(1)*(1-exp(-1)*2);
ER=ER+2*(w(2)+w(3))*exp(-1)/2+2*w(2)*(1-exp(-1)-exp(-1)-exp(-1)/2);
ER=ER+3*w(3)*(1-exp(-1)-exp(-1)-exp(-1)/2);