R统计绘图-线性混合效应模型详解(理论、模型构建、检验、选择、方差分解及结果可视化)

一、基础理论

二、数据准备

三、构建线性混合效应模型(LMMs)

3.1 lme4线性混合效应模型formula

3.2 随机截距模型构建及检验

3.3 随机截距模型分析结果解释及可视化

3.4 随机斜率模型构建、检验及可视化

四、线性混合效应模型选择

4.1 多模型比较

4.2 模型最优子集筛选

一、基础理论

各个数据模型都包含一些假设，当数据满足这些假设时，使用这些模型得到的结果才会更准确。比如广义线性模型要满足“线性”和“独立性”等条件。为了适应更多数据类型，开发出了各种模型，可根据数据情况，选择合适的模型。比如，如果数据不满足“线性”，则可考虑广义可加模型；如果不满足“独立性”，则可以考虑混合效应模型(mixed effect model)。

多水平模型同时包含多个分类因子数据，最主要特点就是非独立性，在多个水平上都存在残差，因此适合混合效应模型，总的来说，其思想就是把高水平上的差异估计出来，这就使得残差变小，估计的结果更为可靠。混合效应模型又称随机效应模型(Random Effect model)，分层线性模型，随机系数模型，方差成分模型等。

比如，一份包含不同施肥处理的多土层微生物数据，其中不同施肥处理与不同土壤深度即是嵌套数据(多水平数据)。

如果用线性模型分析不同施肥处理间微生物群落的差异，则没有考虑到不同土壤深度的微生物群落的差异，暗含了假设：不同土壤深度的微生物群落随不同施肥处理变化的截距与斜率都是相同的。不同土壤深度土壤的微生物群落差异就被线性模型归类到误差中去了。

如何解决这一问题呢？其中一种方法就是使用固定效应模型(Fixed Effect Model)，即将不同土壤深度的微生物群落结构随不同施肥处理变化的截距差异和斜率差异都估计出来。在土壤深度分类较少时可以这么做，将次级分类水平作为虚拟变量回归，3分类，则估计2个截距差异和斜率差异。当次级分类水平过多时，需要估计的参数太多，用虚拟变量就会消耗太多的自由度，估计结果不可靠，此时即可考虑使用混合效应模型。

固定效应与随机效应因子之间没有明显的分类，但显然随机效应因子要是分类数据，且数据跟随机效应存在相关性。有文章推荐随机效应的分类水平最好大于5类，因为当分类水平较少时，模型对方差的估计不太准确。当随机因子大于1个时，随机因子间的关系也需要注意，根据随机因子间关系，可能包括交叉(Crossed)、部分交叉或嵌套(nested)。

混合效应模型也分为线性混合效应模型、广义线性混合效应模型和非线性混合效应模型。此文章介绍使用R中lme4包进行线性混合效应模型分析。

线性混合效应模型假设：

1. 残差应该是正态分布的-可以适当放宽，前提是预测值与残差没有相关性，

2. 残差的方差是同质的-非常重要的假设；

3. 随机效应的观测是相互独立的；

4. 自变量与因变量存在线性关系；

5. 自变量间不存在相关性-方差膨胀因子筛选或者数据降维。

当然，对数据中异常点的检测也是很有必要的。

二、数据准备

此套数据是嵌套数据，包含分类因子depth和tillage。嵌套数据中包含多个分类自变量，数据是非独立性的，模型构建时考虑使用混合效应模型。选择pH为因变量。

# 设置工作路径
#knitr::opts_knit$set(root.dir="D:\\EcoEvoPhylo\\MEM\\LMM")# 使用Rmarkdown进行程序运行
Sys.setlocale('LC_ALL','C') # Rmarkdown全局设置
#options(stringsAsFactors=F)# R中环境变量设置，防止字符型变量转换为因子
library(tidyverse)
library(rstatix)
library(car)
library(lme4)
library(lmerTest) # 模型固定效应系数检验
library(multilevelTools) # 模型诊断检验
library(extraoperators)
library(JWileymisc) # 模型诊断及APAStyler以表格形式输出模型结果
library(effectsize) # 计算标准化回归系数
library(influence.ME) # 检测高影响观测点
library(GGally)

# 2.1 导入数据
env <- read.csv("env.csv",row.names = 1)
env %>% head

# 2.2 计算均值与标准误
env %>%
  group_by(condition) %>%
  get_summary_stats(names(env[4:ncol(env)]),type="mean_se") %>%
  left_join(env[1:3],by = "condition") -> data
data %>% sample_n_by(tillage,size=2)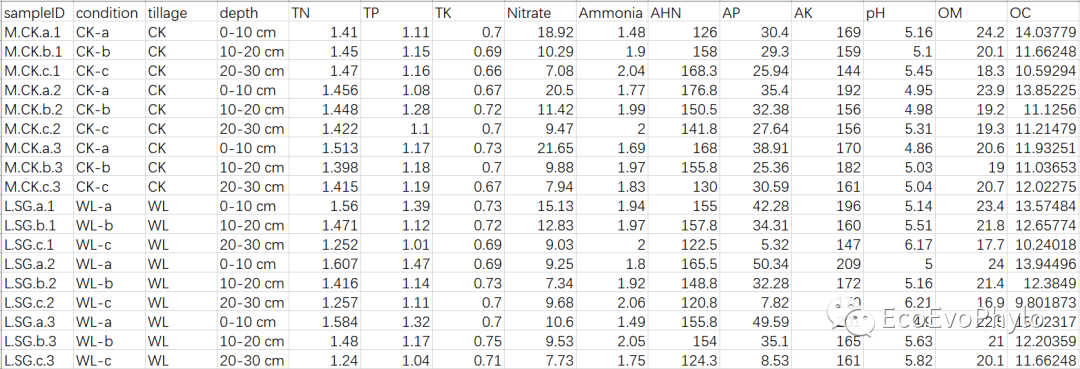

图1|原始数据表，env.csv。

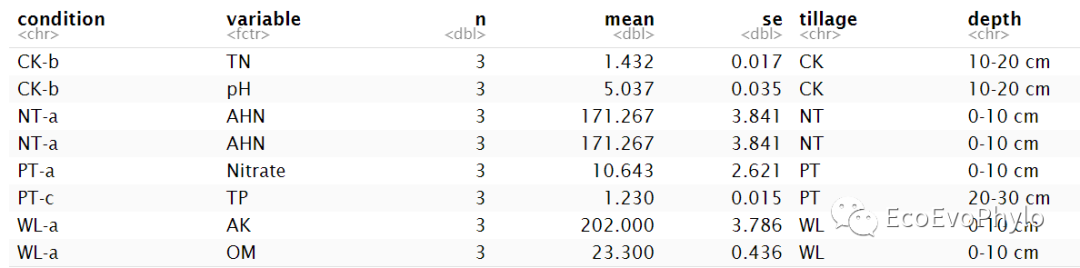
图2|均值-标准误差计算结果，data。

# 2.3 数据探索-查看数据是否适合进行线性混合效应模型分析
## 2.3.1 ICC-组内相关系数计算
icc1 <- iccMixed("pH","depth",env)
icc1
icc2 <- iccMixed("pH","tillage",env)
icc2

图3|组内相关系数计算结果，icc1。intra-class correlation coefficient (ICC)将变量差异分解为组内和组间差异，此处将depth作为随机截距，Sigma列依次为随机截距方差(组间差异)，残差(组内差异)。ICC=0表示差异全部来自组内个体差异，ICC=1表示变量差异全部来自组间，此处ICC=0.5062462表明depth水平间的方差挺大的，可以考虑使用混合效应模型。

## 2.3.2 计算有效样本大小
nEffective(n = length(unique(env$depth)),
           k = nrow(env)/length(unique(env$depth)),
           dv = "pH",
           id = "depth",data=env
                  )

图4|effective sample size。对数据提供的有效独立样本数量的估计。N为独立的样本数量，k为每个独立样本的重复测量次数。

## 2.3.3 因变量分布、极端值探索
### 将因变量按照分类因子进行均值分解
#### depth
tmp1 <- meanDecompose(pH ~ depth, data = env)
tmp1
tmp1$`pH by depth`
tmp1$`pH by residual`
plot(testDistribution(tmp1[["pH by depth"]]$X,
                      extremevalues = "theoretical", ev.perc = .001),
     varlab = "Between Depth")

plot(testDistribution(tmp1[["pH by residual"]]$X,
                      extremevalues = "theoretical", ev.perc = .001),
     varlab = "Within Depth")#图中黑色点表示极端值。

#### tillage
tmp2 <- meanDecompose(pH ~ tillage, data = env)
tmp2
do.call(cowplot::plot_grid, c(lapply(names(tmp2), function(x) {
  plot(JWileymisc::testDistribution(tmp2[[x]]$X), plot = FALSE, varlab = x)$Density
}), ncol = 1))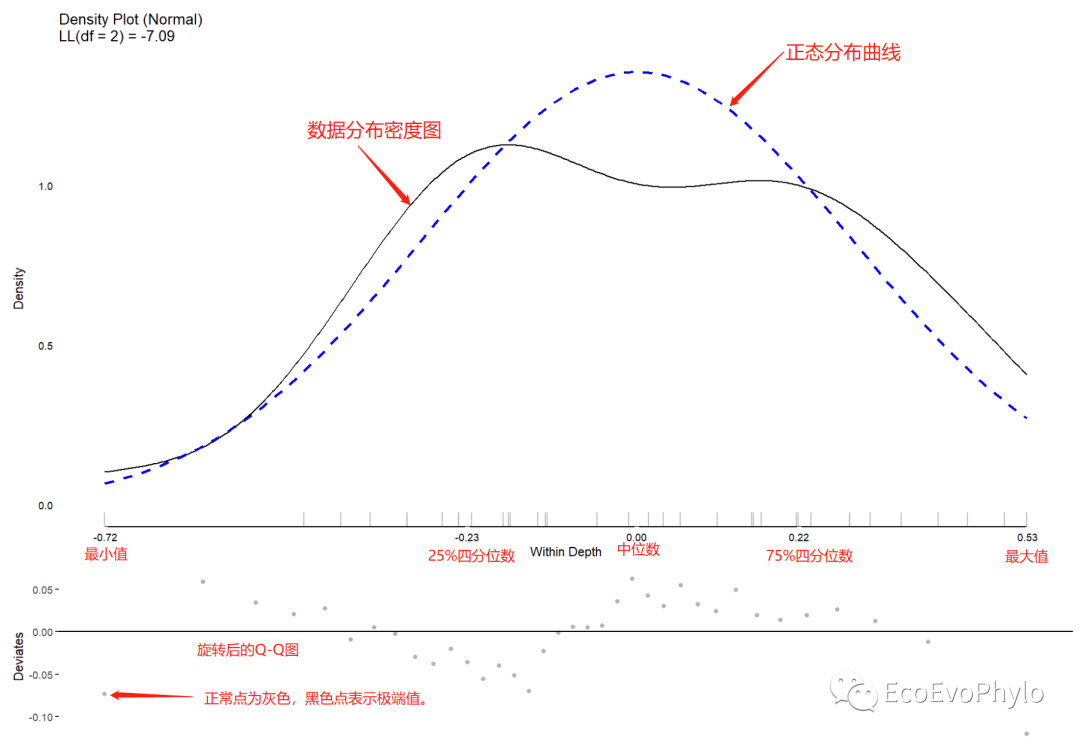

图5|均值分解图，Within Depth。

## 2.3.4 散点图可视化数据分布趋势
### width format转为long format
(env %>%
  gather(key = "variable",value = "value",-condition,-tillage,-depth) %>%
  rstatix::reorder_levels(variable,
                 order =c("pH","OM", "OC", 
                          "Ammonia", "Nitrate","AHN",  
                          "TN", "TP", "TK", 
                          "AP", "AK"
                           )) -> data.p)

### 设置颜色
col1 <- colorRampPalette(colors =c("#56B1F7","#132B43"),space="Lab") 

### 绘制分面-分组散点图
(data.p %>%  ggplot2::ggplot(aes(
  x = factor(tillage,levels=c("CK","WL","NT","PT")),
  y = value,
  color= factor(depth,levels = unique(data.p$depth))))+
  geom_point(
    position = position_dodge(0.8), #调整site之间的宽度距离。
    width = 0.5,size = 1
  )+
  scale_color_manual(name = "Depth",
                     # values = ggsci::pal_d3("category10")(10),
                     values = col1(3),
                     breaks = c(unique( as.character(data.p$depth) )))+
  facet_wrap(.~variable,ncol = 4,scales = "free")+
  labs(x = NULL, y = NULL) -> p1) # 绘图函数加上括号，赋值给变量的同时，会在屏幕上显示。

### 输出pdf图到本地
ggsave("p1.pdf", p1, device = "pdf",width = unit(10,"cm"),height = unit(8,"cm"))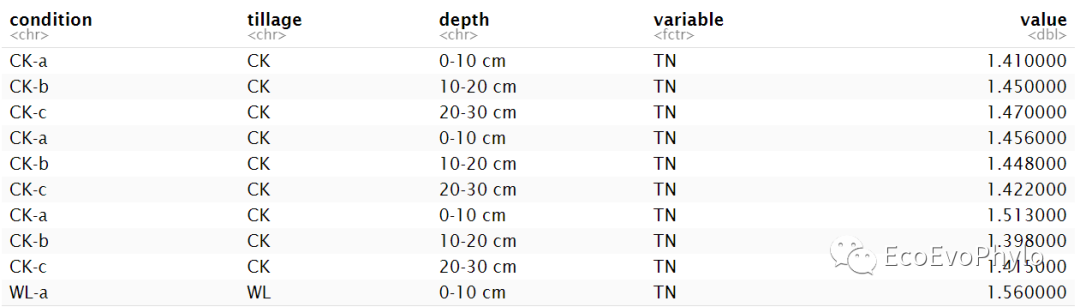

图6|long format格式数据表，data.p。

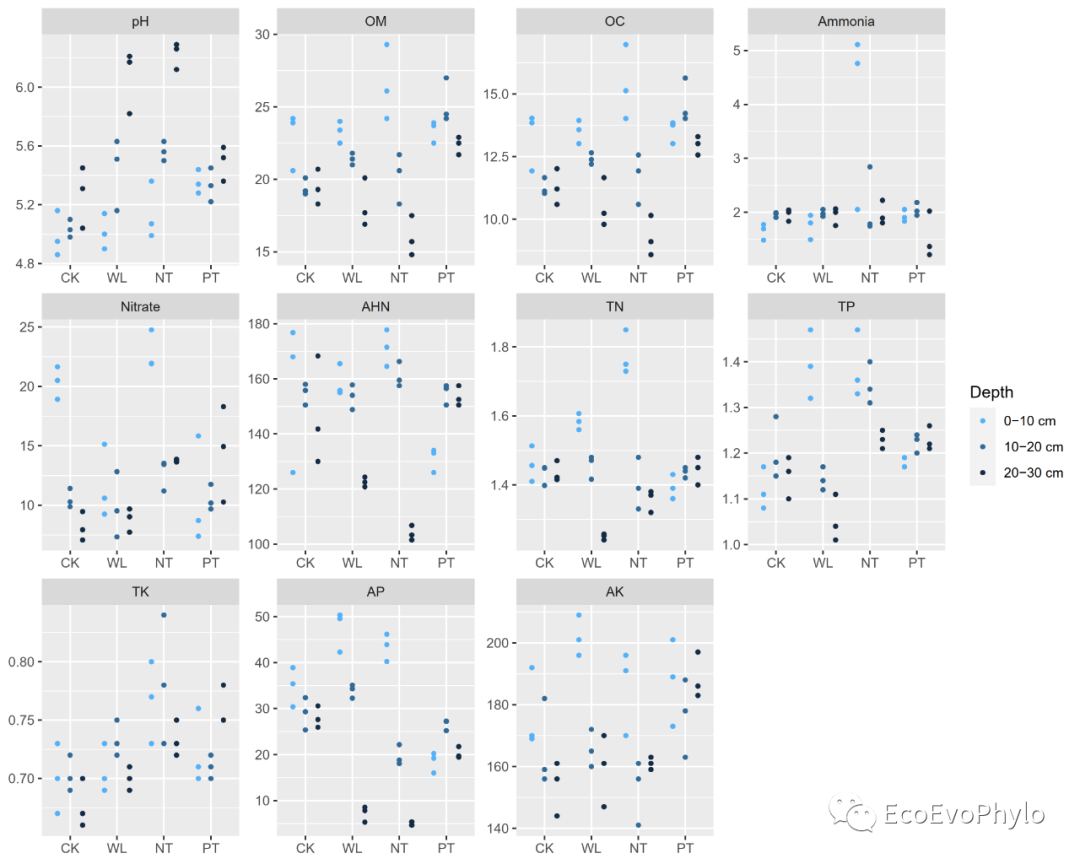
图7|可视化pH数据分布，p1.pdf。

## 2.3.5 绘制变量相关性图
### 设置绘图颜色
cols <- ggsci::pal_jco()(7) 
### 绘制相关性图
my_density <- function(data, mapping) {
 ggplot(data = data, mapping = mapping) +
 geom_density() 
} # 自定义函数

(
 ggpairs(env,columns = 4:14, 
 ggplot2::aes(color = tillage), # 按分组信息分别着色、计算相关性系数和拟合
 upper = list(continuous = "cor"), 
 lower = list(continuous = wrap("smooth",method = "lm",se = FALSE)), # se = FALSE,不展示置信区间 
 diag = list(continuous = my_density))+
 ggplot2::scale_color_manual(values = cols)+
 theme_bw() -> p2
 )

### 输出pdf图到本地
pdf("p2.pdf",height = 20,width = 20,family = "Times")
print(p2)
dev.off()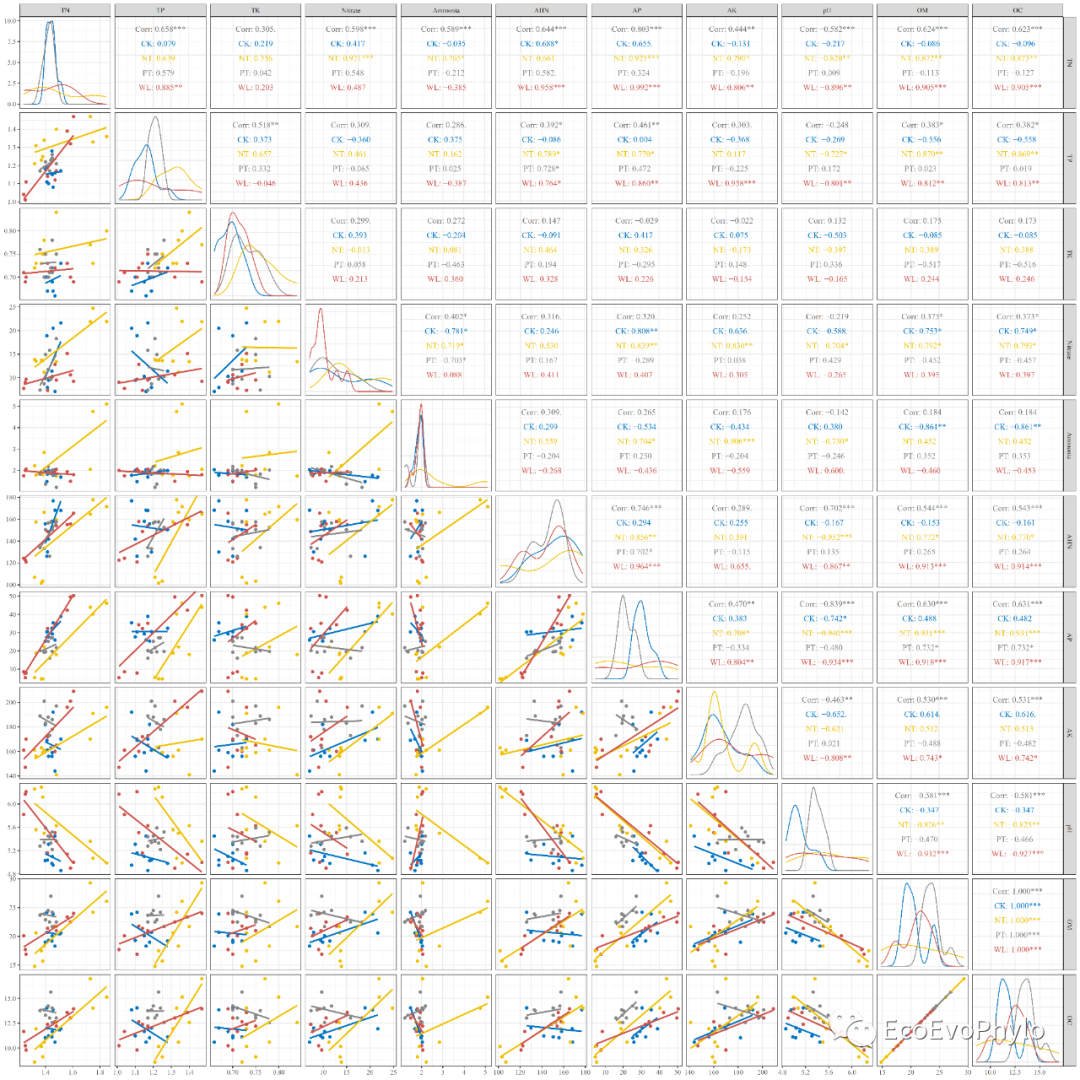

图8|变量相关性线性拟合图，p2.pdf。由图可知，很多两两变量的关系在tillage水平中的截距和斜率是不一致的。

三、构建线性混合效应模型(LMMs)

混合效应模型是指包含固定效应和随机效应的模型，固定效应部分就是线性模型模式，随机效应可以分为随机截距模型和随机斜率模型两大类。固定效应因子与随机效应因子没有很严格的区分，更多是根据自己的研究目的进行设置，最后模型都要满足线性混合模型的假设以及符合科学性。

此处使用lme4执行线性混合效应模型，(1+depth)表示depth是随机因子，截距随机。lme4包提供了进行线性混合效应模型、广义线性混合效应模型和非线性混合效应模型拟合和分析的功能。nlme包也可用于混合效应模型的建模。随机效应项在函数表达式中表现为(expr|factor)，expr是一个线性或广义线性等模型公式，factor是随机因子。lme4中用不同的formula区分交叉或嵌套数据。

此过程是模型矩阵与分组因子的一种特殊交互，用以确保固定因子模型矩阵对于分组因子各水平都有不同的影响。分组因子效应被建模为未观察到的随机变量，而不是未知的固定参数。随机截距模型的截距的平均值和标准差是要估计的参数，模型将随机效应的任何非零均值合并为固定效应参数。函数默认执行限制性极大似然估计(REML)，REML假设固定效应结构是正确的,在比较具有不同固定效应的模型时，应该使用最大似然(ML)。因为ML不依赖于固定效应的系数。但ML对两个具有嵌套随机结构的模型进行比较时，对方差项的估计量存在偏差。因此，具有相同固定效应的模型，使用REML比较随机效应不同的模型。

模型(固定效应系数和模型比较)显著性检验方法可选(效果从弱到强)：

1）Wald Z-tests，固定效应系数显著性检验，适合大数据集；

2）Wald t-tests (but LMMs need to be balanced and nested)；

3）Likelihood ratio tests，只能用于ML拟合模型，可比较固定效应或随机效应不同的两个模型，那个能更好的拟合数据；

4) Kenward-Roger and Satterthwaite approximations for degrees of freedom，可比较两个固定效应模型的差异显著性;

5）MCMC，不适合随机斜率模型;

6）parametric bootstrap confidence intervals。

当样本量足够时p值获取可以通过LRT或Wald t检验模型，但样本量较少时更推荐使用Kenward-Roger(只能用于REML)，Satterthwaite approximations(REML或ML)或parametric bootstrap。

3.1 lme4线性混合效应模型formula

随机截距模型：模型中只包含随机截距；随机斜率模型：模型中包含随机斜率。

# 3.1.1 线性回归模型
fm0 <- lm(pH ~ tillage + AP, 
           data = env)
fm0 %>% summary


# 3.1.2 随机截距模型-depth的各水平都有对应的截距，模型会估计这些截距的均值和标准差。
control <- lmerControl(
  optCtrl = list(
   algorithm = "NLOPT_LN_NELDERMEAD",
   xtol_abs = 1e-12,
   ftol_abs = 1e-12,
   check.conv.singular = .makeCC(action = "ignore", 
                                 tol = 1e-12)
  )
)

fm1 <- lmer(pH ~ tillage + AP + (1|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm1 %>% summary

# 3.1.3 随机截距模型-添加先验prior截距均值
fm2 <- lmer(pH ~ tillage + AP + offset(AP) + (1|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm2 %>% summary


# 3.1.4 混合效应模型：相关随机系数和截距模型
##lme4假设同一随机效应项的所有系数项是相关的。
fm3 <- lmer(pH ~ tillage + AP + (1+tillage|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm3 %>% summary


# 3.1.5 指定不相关随机系数和截距模型-相当于(tillage||depth)
fm4 <- lmer(pH ~ tillage + AP + (1|depth)+(0+tillage|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm4 %>% summary


# 3.1.6 考虑交互效应的随机截距模型-相当于(1|tillage) +(1|tillage:depth)。
##depth必须嵌套于tillage,不同tillage水平，depth间的pH不独立且具有差异。
fm5 <- lmer(pH ~ AP + (1|tillage/depth),
           data = env,
           REML = FALSE,
           control = control)
fm5 %>% summary

# 3.1.7 两组分类因子混合效应模型-如果同一样本在两个随机因子处都有观测， 则是交叉数据。
##将tillage与depth合并因子condition纳入分析，则是交叉数据。
##此处观察的是所有实验处理(tillage)和采样区域(condition)的对因变量的影响。
fm6 <- lmer(pH ~ AP + (1|tillage) + (1|condition), 
           data = env,
           REML = FALSE,
           control = control) # 可以与fm6进行比较，观察两者差异。
fm6 %>% summary


# 3.1.8 混合效应模型-depth各水平在tillage和AP都有不同斜率和不同截距。
fm7 <- lmer(pH ~ AP + tillage + (tillage + AP|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm7 %>% summary


# 3.1.9 随机斜率模型
fm8 <- lmer(pH ~ tillage + AP +(0 + tillage|depth), # 0表示固定截距。
           data = env,
           REML = FALSE,
           control = control)
fm8 %>% summary

出现