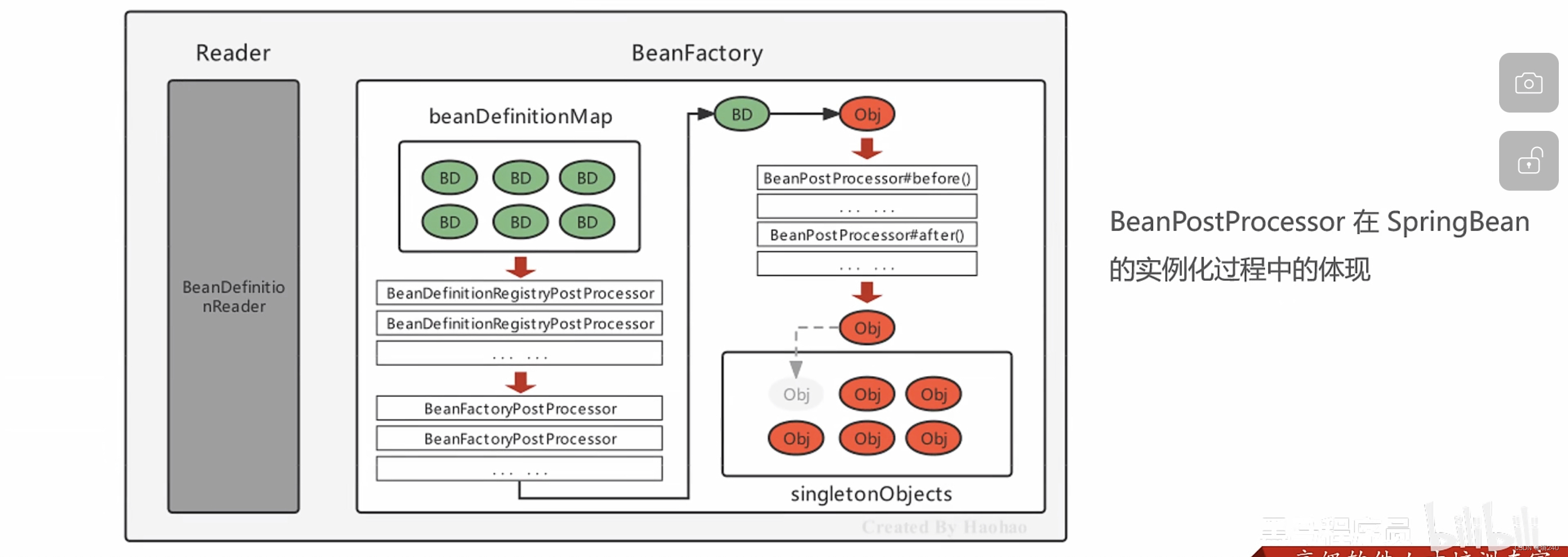
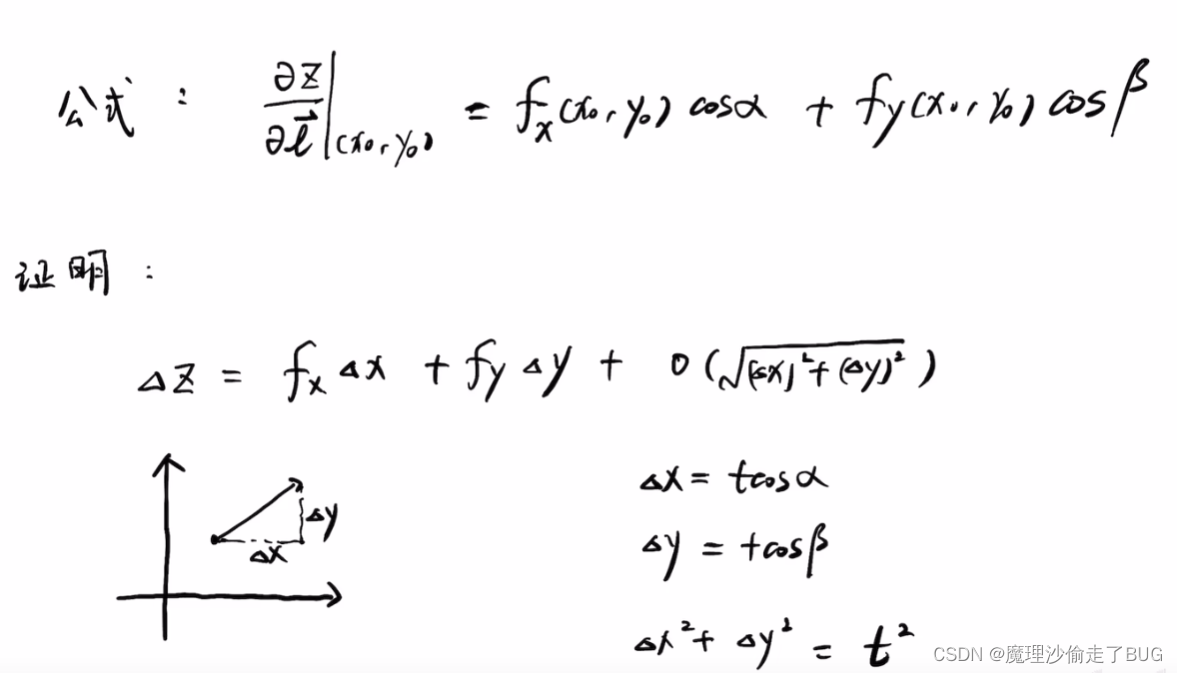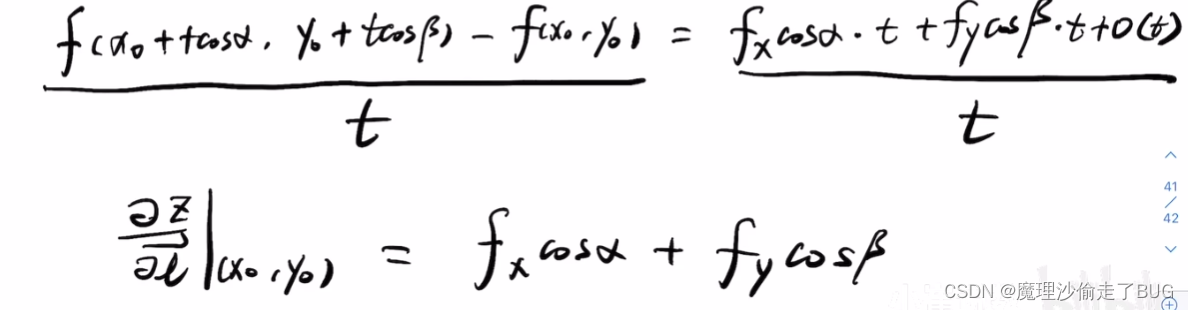课程地址和说明
线性代数实现p4
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
本节是第一篇
矩阵计算
标量导数



导数刻画的是函数在某点的瞬时变化率
这东西都是考研学过的,快速略过,如果忘记直接查表,导数定义如下:


亚导数
就是不可导点如果是左右导数不相等的情况下,就在该点取左导数或者右导数的值作为导数值,比如
f
(
x
)
=
∣
x
∣
f(x)=|x|
f(x)=∣x∣

那个其实应该是
a
∈
{
−
1
,
1
}
a\in \left\{-1,1\right\}
a∈{−1,1}
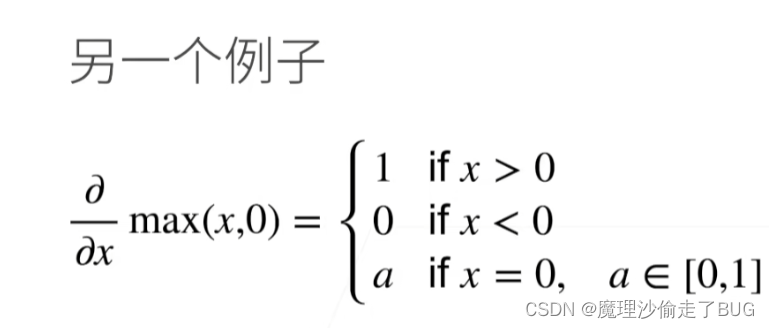
偏导数
本章节参考视频:【多元微分专题】第六期:方向导数和梯度的直观理解
在多元函数
f
(
x
,
y
,
.
.
.
)
f(x,y,...)
f(x,y,...)(以2个自变量的多元函数
f
(
x
,
y
)
f(x,y)
f(x,y)为例子,此时为3维坐标系),所谓的偏导数就是曲面上某点
(
x
0
,
y
0
)
处
(x_{0},y_{0})处
(x0,y0)处沿着
x
x
x轴或
y
y
y轴的正方向的变化率,即:
f
x
(
x
0
,
y
0
)
=
lim
△
x
→
0
f
(
x
0
+
△
x
,
y
0
)
−
f
(
x
0
,
y
0
)
△
x
f
y
(
x
0
,
y
0
)
=
lim
△
x
→
0
f
(
x
0
,
y
0
+
△
y
)
−
f
(
x
0
,
y
0
)
△
y
f_{x}(x_{0},y_{0})=\lim_{ \bigtriangleup {x} \to 0} \frac{f(x_{0}+\bigtriangleup {x},y_{0})-f(x_{0},y_{0})}{\bigtriangleup {x}}\\ f_{y}(x_{0},y_{0})=\lim_{ \bigtriangleup {x} \to 0} \frac{f(x_{0},y_{0}+\bigtriangleup {y})-f(x_{0},y_{0})}{\bigtriangleup {y}}
fx(x0,y0)=△x→0lim△xf(x0+△x,y0)−f(x0,y0)fy(x0,y0)=△x→0lim△yf(x0,y0+△y)−f(x0,y0)
从几何上直观地看就是:

方向导数
上述多元函数不一定在按某个固定轴方向上有变化率,还可以按任意方向上变化,由此引出方向导数的概念。
方向余弦
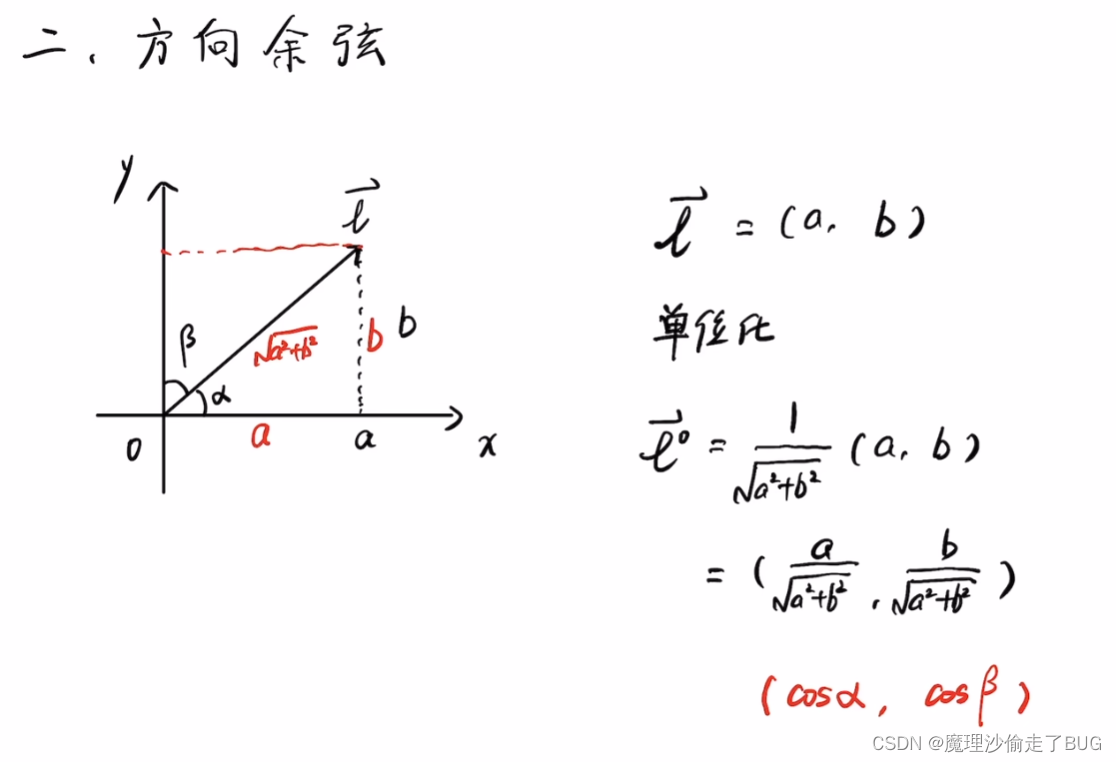
方向导数
一个多元函数在某点处的值入下图黑色点所示:

该点在xOy面的投影点为蓝色的点,这个函数可以沿着这个投影点做向量起始点的在xOy平面上的任意向量的方向上发生变化:
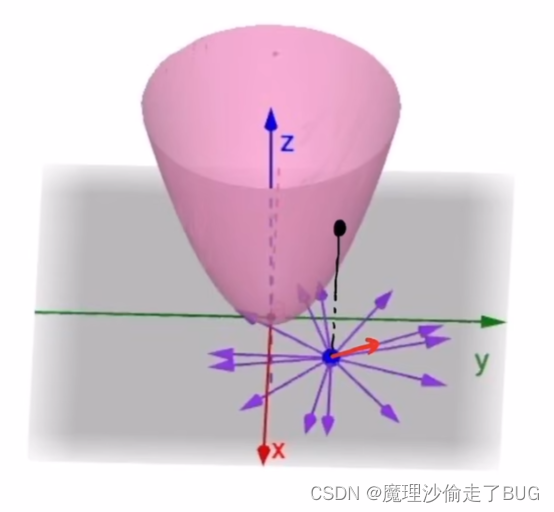
假如在该点处,函数按照下图中紫色向量的方向变化:
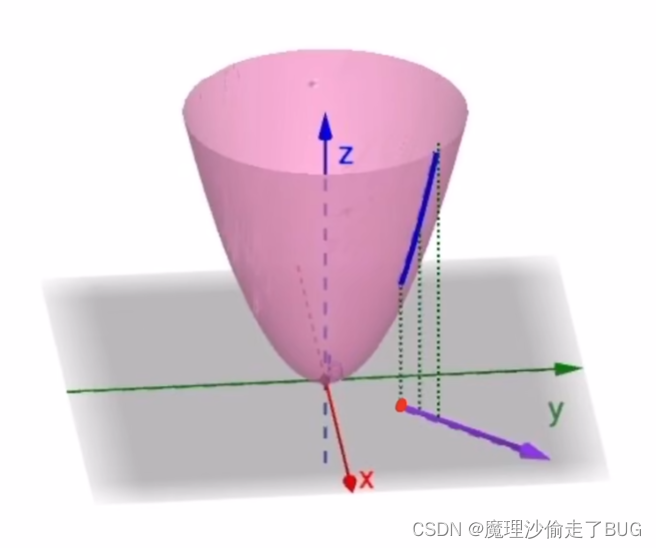
那么它会在向量方向上投影出一段曲线(以这个向量所在平面切这个曲面),由此得到了如下图的在该点处对应投影曲线的切线:
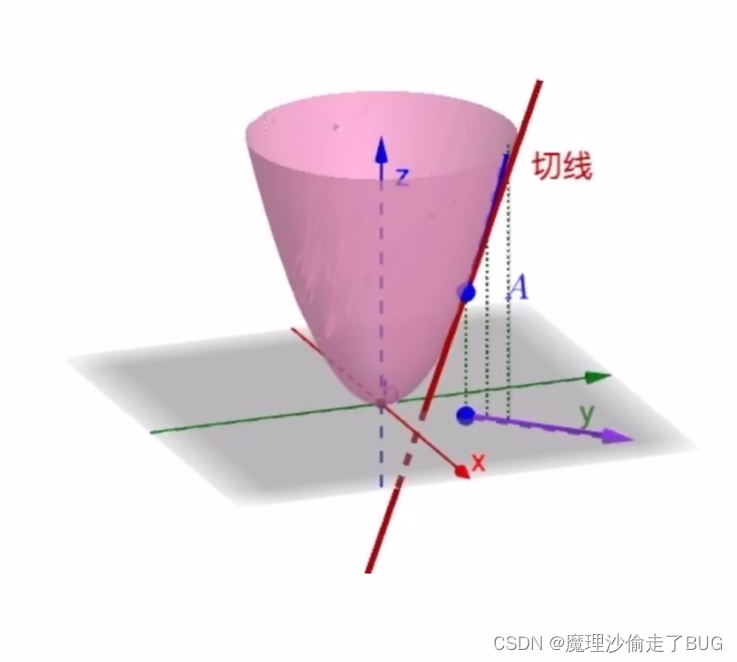
当该向量变换方向的时候,其在紫色向量所在平面1与曲线相交在平面1上的曲线在该点处的切线斜率也会发生变化,它可以360°任意方向变化,如下面三张图所示:
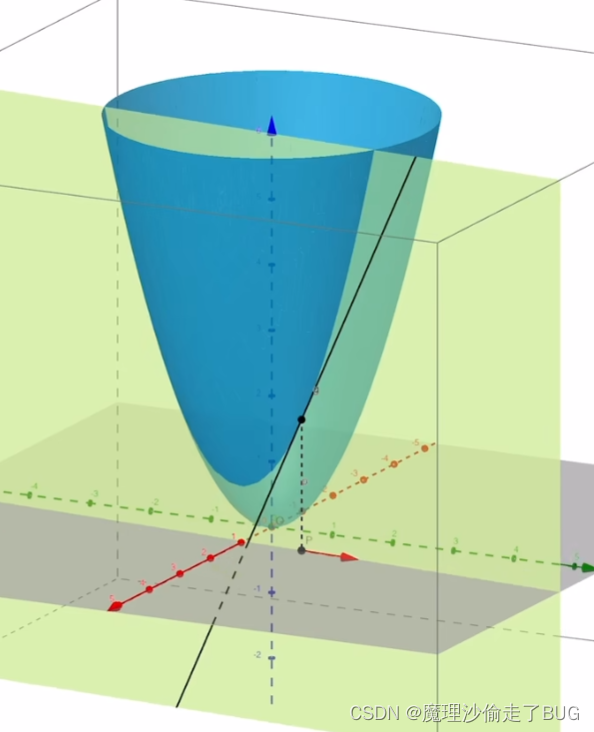
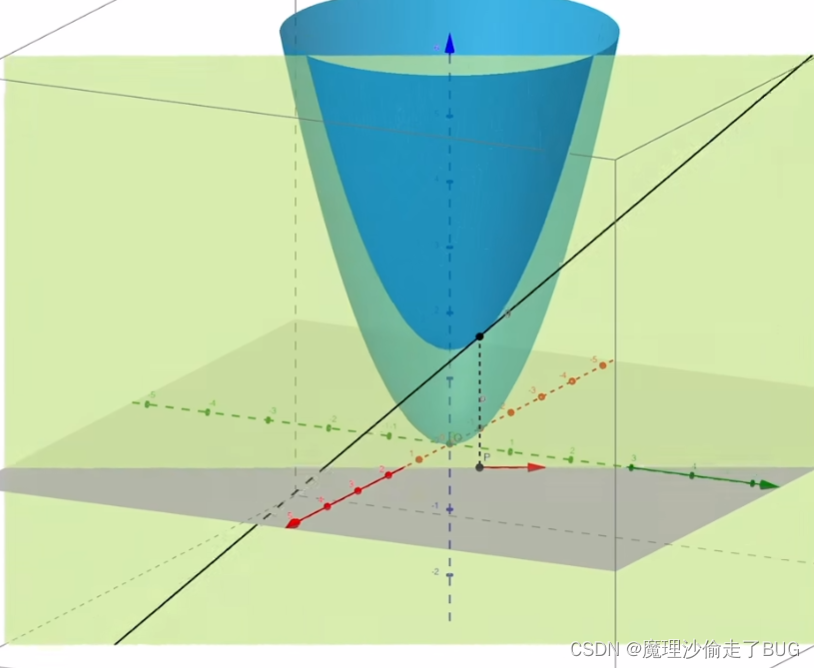
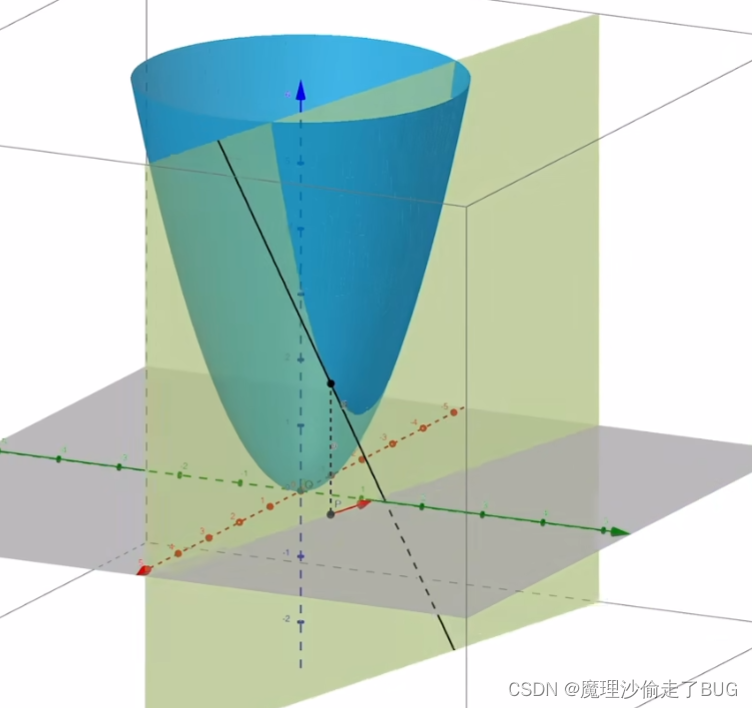
如上图所示,单位向量可以写成方向余弦形式。
当自变量从A点走到B点,因变量也会发生
△
Z
\bigtriangleup Z
△Z的改变。
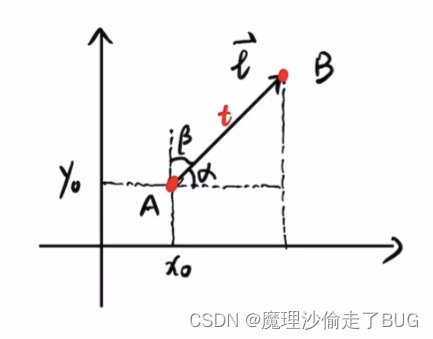
- 方向导数的定义如下:
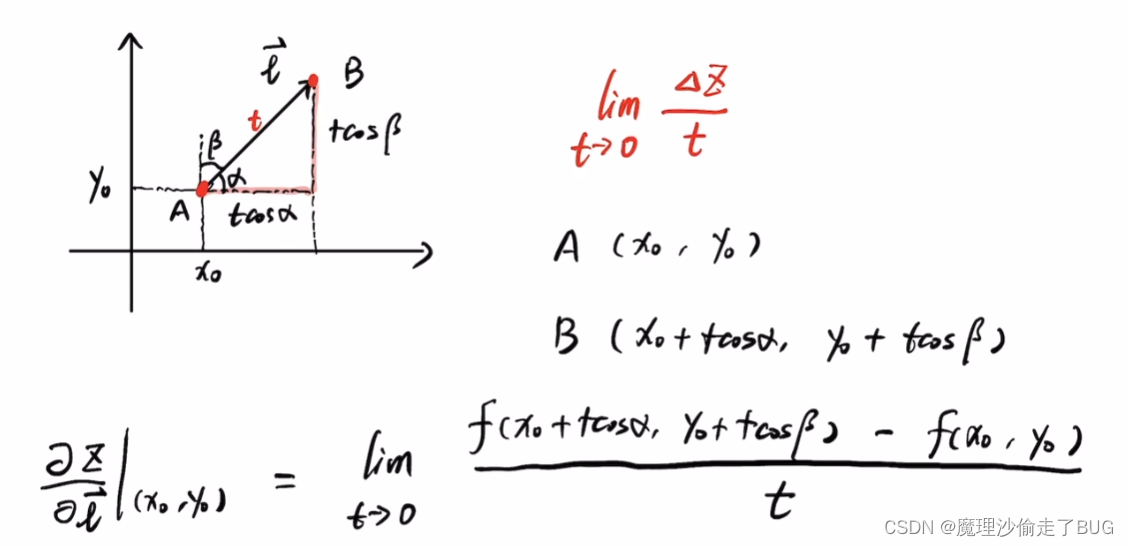
所以说偏导数是方向导数的特例,是让其沿着xOy平面中的 x x x轴的方向向量或 y y y轴的方向向量计算变化率。
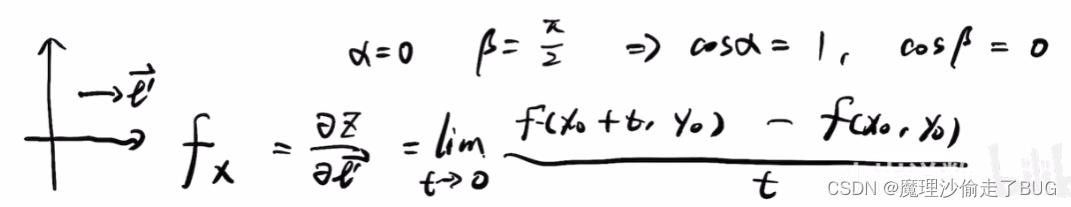
方向导数的计算