LESS的叶绿素荧光模拟实现与操作
- 前情提要
- FLUSPECT模型
- 荧光的三维面元冠层辐射传输过程
- 日光诱导叶绿素荧光模拟
前情提要
本文默认您对LESS (LargE-Scale remote sensing data and image Simulation framework) 模型和叶绿素荧光(Sun-Induced chlorophyll Fluorescence, SIF)有一定的了解。当然,您也可以在这里下载中文的简明手册,了解更多关于三维辐射模型的原理及LESS操作。
FLUSPECT模型
LESS在FLUSPECT基础上,模拟了多角度、多成像模式的冠层叶绿素荧光模拟。
FLUSPECT在PROSPECT的基础上,除了模拟叶片的反射率和透射率,还可模拟叶片正向和背向激发的叶绿素荧光。模型考虑了荧光在叶片中的再吸收。使用一种快速层加倍算法,快速求解12。
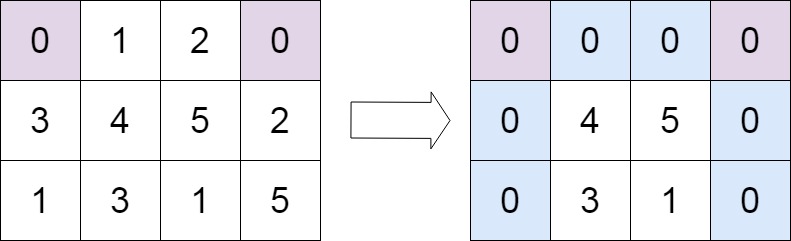
FLUSPECT通过荧光激发矩阵( E F 211 × 351 EF_{211\times 351} EF211×351将400 – 750 nm的激发光谱( E 351 × 1 E_{351\times 1} E351×1)转化为640 – 850 nm的荧光光谱( F 211 × 1 F_{211\times 1} F211×1),光谱间隔为1 nm。受限于 E F 211 × 351 EF_{211\times 351} EF211×351的光谱采样间隔,在LESS中,模拟荧光时规定,激发光谱与荧光光谱的光谱间隔相等且固定,并且为整数个nm。 E F 211 × 351 EF_{211\times 351} EF211×351重采样到其他光谱间隔的方式比较特殊,需要考虑激发光谱的累乘相加如何在其他光谱间隔上实现。这里不加推导地给出重采样方法: E F u , v ~ = ∑ ∑ E F i , j i n c , i n c ∈ N + \widetilde{EF_{u,v}}=\frac{\sum\sum EF_{i,j}}{inc},inc\in\mathbb{N}^{+} EFu,v =inc∑∑EFi,j,inc∈N+其中, E F i , j EF_{i,j} EFi,j为边缘补0后,与重采样的 E F ~ \widetilde{EF} EF 对齐的原始矩阵,inc为采样后波长间隔。下图展示了重采样带来的偏差,以5 nm间隔采样,能够较好地平衡模拟耗时与精度需求。

荧光的三维面元冠层辐射传输过程
在LESS中,沿用了“光线束(Ray bundle)”的概念,即每条光线(每个光子)是包含了多个波段的能量束。为了记录普通光子和荧光光子,需要生成波段范围在400 – 850 nm的光子,共n个波段,记普通光子携带的能量为 L t o t a l , 1 × n L_{total,1\times n} Ltotal,1×n,PSI荧光光子为 L P S I , 1 × n L_{PSI,1\times n} LPSI,1×n,PSII荧光光子为 L P S I I , 1 × n L_{PSII,1\times n} LPSII,1×n。其中,400 – 750 nm的能量会激发640 – 850 nm的叶片荧光。
此时, L t o t a l , 1 × n L_{total,1\times n} Ltotal,1×n激发 L P S I , 1 × n L_{PSI,1\times n} LPSI,1×n和 L P S I I , 1 × n L_{PSII,1\times n} LPSII,1×n的过程需要通过扩充后的荧光激发矩阵( M n × n M_{n\times n} Mn×n)描述,光子的散射过程通过散射矩阵描述,它们表示如下: M n × n = [ O E F ~ T O O ] , R n × n = d i a g { r 1 , r 2 , r 3 , . . . , r n } , M_{n\times n}=\begin{bmatrix}O&\widetilde{EF}^\mathrm{T}\\O&O\end{bmatrix},R_{n\times n}=diag\{r_1,r_2,r_3,...,r_n\}, Mn×n=[OOEF TO],Rn×n=diag{r1,r2,r3,...,rn},其中, E F ~ T \widetilde{EF}^\mathrm{T} EF T表示光线交点处的重采样荧光激发矩阵的转置,并认为后向荧光与反射光线一同传输,前向荧光与透射光线一同传输,r表示光线交点处的反射率或透过率。当r取反射率时, E F ~ \widetilde{EF} EF 取后向荧光激发矩阵;当r取透过率时, E F ~ \widetilde{EF} EF 取前向荧光激发矩阵。则荧光激发过程描述如下: { L P S I , 1 × n = L t o t a l , 1 × n × M P S I , n × n L P S I I , 1 × n = L t o t a l , 1 × n × M P S I I , n × n , \left.\left\{\begin{matrix}L_{PSI,1\times n}=L_{total,1\times n}\times M_{PSI,n\times n}\\L_{PSII,1\times n}=L_{total,1\times n}\times M_{PSII,n\times n}\end{matrix}\right.\right., {LPSI,1×n=Ltotal,1×n×MPSI,n×nLPSII,1×n=Ltotal,1×n×MPSII,n×n,光子散射过程描述如下: L t o t a l , 1 × n = L t o t a l , 1 × n × R n × n 。 L_{total,1\times n}=L_{total,1\times n}\times R_{n\times n}。 Ltotal,1×n=Ltotal,1×n×Rn×n。那么,当光线与能发射荧光的材质相交时,各种光子能量变化过程如下: { L P S I o u t , 1 × n = L t o t a l i n , 1 × n × M P S I , n × n L P S I I o u t , 1 × n = L t o t a l i n , 1 × n × M P S I I , n × n L t o t a l o u t , 1 × n = L t o t a l i n , 1 × n × R n × n + L P S I o u t , 1 × n + L P S I I o u t , 1 × n = L t o t a l i n , 1 × n × ( R n × n + M P S I , n × n + M P S I I , n × n ) , \left.\left\{\begin{array}{c}L_{PSIout,1\times n}=L_{totalin,1\times n}\times M_{PSI,n\times n}\\L_{PSIIout,1\times n}=L_{totalin,1\times n}\times M_{PSII,n\times n}\\L_{totalout,1\times n}=L_{totalin,1\times n}\times R_{n\times n}+L_{PSIout,1\times n}+L_{PSIIout,1\times n}\\=L_{totalin,1\times n}\times\left(R_{n\times n}+M_{PSI,n\times n}+M_{PSII,n\times n}\right)\end{array}\right.\right., ⎩ ⎨ ⎧LPSIout,1×n=Ltotalin,1×n×MPSI,n×nLPSIIout,1×n=Ltotalin,1×n×MPSII,n×nLtotalout,1×n=Ltotalin,1×n×Rn×n+LPSIout,1×n+LPSIIout,1×n=Ltotalin,1×n×(Rn×n+MPSI,n×n+MPSII,n×n),不妨记 T n × n = R n × n + M P S I , n × n + M P S I I , n × n T_{n\times n}=R_{n\times n}+M_{PSI,n\times n}+M_{PSII,n\times n} Tn×n=Rn×n+MPSI,n×n+MPSII,n×n。
在每个交点处计算荧光光子是可行的,但计算量庞大,一般不在每处计算荧光光子能量。一般采取累乘转移矩阵的方式,计算光源能量与传感器接受能量之间的转化矩阵。
考虑一条有荧光的光线前向追踪路径中,两个面片对光子能量的改变,如下图。
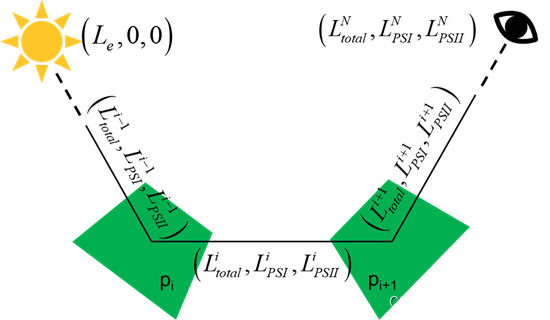
对于荧光来说,光线与荧光面片i相交后,除了激发的荧光,还有散射的荧光,则出射的光线为:
{
L
P
S
I
i
=
L
t
o
t
a
l
i
−
1
×
M
P
S
I
i
+
L
P
S
I
i
−
1
×
R
i
L
P
S
I
I
i
=
L
t
o
t
a
l
i
−
1
×
M
P
S
I
I
i
+
L
P
S
I
I
i
−
1
×
R
i
L
t
o
t
a
l
i
=
L
t
o
t
a
l
i
−
1
×
R
i
+
L
P
S
I
i
+
L
P
S
I
I
i
\begin{cases}L_{PSI}^i=L_{total}^{i-1}\times M_{PSI}^i+L_{PSI}^{i-1}\times R^i\\L_{PSII}^i=L_{total}^{i-1}\times M_{PSII}^i+L_{PSII}^{i-1}\times R^i\\L_{total}^i=L_{total}^{i-1}\times R^i+L_{PSI}^i+L_{PSII}^i\end{cases}
⎩
⎨
⎧LPSIi=Ltotali−1×MPSIi+LPSIi−1×RiLPSIIi=Ltotali−1×MPSIIi+LPSIIi−1×RiLtotali=Ltotali−1×Ri+LPSIi+LPSIIi面片i出射的光线与面片i+1相交后,出射的光线为:
{
L
P
S
I
i
+
1
=
L
t
o
t
a
l
i
×
M
P
S
I
i
+
1
+
L
P
S
I
i
×
R
i
+
1
L
P
S
I
I
i
+
1
=
L
t
o
t
a
l
i
×
M
P
S
I
I
i
+
1
+
L
P
S
I
I
i
×
R
i
+
1
L
t
o
t
a
l
i
+
1
=
L
t
o
t
a
l
i
×
R
i
+
1
+
L
P
S
I
i
+
1
+
L
P
S
I
I
i
+
1
。
\begin{cases}L_{PSI}^{i+1}=L_{total}^{i}\times M_{PSI}^{i+1}+L_{PSI}^{i}\times R^{i+1}\\L_{PSII}^{i+1}=L_{total}^{i}\times M_{PSII}^{i+1}+L_{PSII}^{i}\times R^{i+1}\\L_{total}^{i+1}=L_{total}^{i}\times R^{i+1}+L_{PSI}^{i+1}+L_{PSII}^{i+1}\end{cases}。
⎩
⎨
⎧LPSIi+1=Ltotali×MPSIi+1+LPSIi×Ri+1LPSIIi+1=Ltotali×MPSIIi+1+LPSIIi×Ri+1Ltotali+1=Ltotali×Ri+1+LPSIi+1+LPSIIi+1。
可以看到,光线传输过程保持了较好的一致性。如果将一条光线的三个组分拼接成一个3×n的行向量,表示为 ( L t o t a l , L P S I , L P S I I ) \left(L_{total},L_{PSI},L_{PSII}\right) (Ltotal,LPSI,LPSII),那么在面片i处出射的光线能量可表示为: ( L t o t a l i , L P S I i , L P S I I i ) 1 × 3 n = ( L t o t a l i − 1 , L P S I i − 1 , L P S I I i − 1 ) 1 × 3 n × [ T i M P S I i M P S I I i O R i O O O R i ] 3 n × 3 n = ( L t o t a l i − 1 × T i , L t o t a l i − 1 × M P S I i + L P S I i − 1 × R i , L t o t a l i − 1 × M P S I I i + L P S I I i − 1 × R i ) 。 \left(L_{total}^i,L_{PSI}^i,L_{PSII}^i\right)_{1\times3n}=\left(L_{total}^{i-1},L_{PSI}^{i-1},L_{PSII}^{i-1}\right)_{1\times3n}\times\left[\begin{matrix}T^i&M_{PSI}^i&M_{PSII}^i\\O&R^i&O\\O&O&R^i\end{matrix}\right]_{3n\times3n}\\=\left(L_{total}^{i-1}\times T^i,L_{total}^{i-1}\times M_{PSI}^i+L_{PSI}^{i-1}\times R^i,L_{total}^{i-1}\times M_{PSII}^i+L_{PSII}^{i-1}\times R^i\right)。 (Ltotali,LPSIi,LPSIIi)1×3n=(Ltotali−1,LPSIi−1,LPSIIi−1)1×3n× TiOOMPSIiRiOMPSIIiORi 3n×3n=(Ltotali−1×Ti,Ltotali−1×MPSIi+LPSIi−1×Ri,Ltotali−1×MPSIIi+LPSIIi−1×Ri)。
从上面两次光线能量的变化中,可以总结出一条光线,从光源发出到传感器接收整个过程中,能量的变化。从光源发出的光线没有荧光成分,表示为 ( L e , 0 , 0 ) \left(L_{e},0,0\right) (Le,0,0),那么到达传感器的光线能量为: ( L t o t a l N , L P S I N , L P S I I N ) 1 × 3 n = ( L e , 0 , 0 ) 1 × 3 n × ∏ i = 1 N [ T i M P S I i M P S I I i O R i O O O R i ] 3 n × 3 n 。 (L_{total}^{N},L_{PSI}^{N},L_{PSII}^{N})_{1\times3n}=\begin{pmatrix}L_{e},0,0\end{pmatrix}_{1\times3n}\times\prod_{i=1}^{N}\begin{bmatrix}T^{i}&M_{PSI}^{i}&M_{PSII}^{i}\\O&R^{i}&O\\O&O&R^{i}\end{bmatrix}_{3n\times3n}。 (LtotalN,LPSIN,LPSIIN)1×3n=(Le,0,0)1×3n×i=1∏N TiOOMPSIiRiOMPSIIiORi 3n×3n。
至此,得到传感器处,一条光线中的荧光能量和包含荧光的总辐射能量3。LESS在此基础上,精简了计算流程,大幅提高了荧光模拟效率。
日光诱导叶绿素荧光模拟
目前,LESS在FLUSPECT基础上模拟了区分/不区分光系统I和II的多角度、多成像模式的冠层叶绿素荧光模拟。用户只需将【Sensor】【Products】【Chl.F】置为非“No”,并给发射荧光的object赋上荧光光谱,即由FLUSPECT模型生成的光谱,其余操作与模拟BRF无异,即可模拟叶绿素荧光。

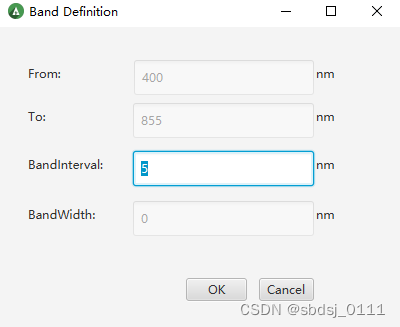
【Sensor】【Products】【Chl.F】置为非“No”后,【Spectral bands】不允许更改,固定为400 nm起,以整数波长间隔增长至最多(不含)855 nm,可通过【Spectral bands】右侧的【Define…】按钮设置整数波长间隔。
LESS中内置了两个版本的FLUSPECT,分别为Fluspect_B_CX_P6(区分PSI和PSII荧光)和Fluspect_B_CX_PRO(不区分PSI和PSII荧光),用户将【Sensor】【Products】【Chl.F】选为“Split PSI PSII”时使用前者,选为“Combine”时使用后者。两个模型对干物质含量和荧光量子效率的处理有些许不同,前者不区分干物质类别,但区分PSI和PSII的荧光量子效率,后者可以区分碳基干物质和氮基干物质,但不区分PSI和PSII的荧光量子效率。需要注意的是,只有干物质含量设为0时,后者才能区分干物质类别,否则不区分。当【Sensor】【Products】【Chl.F】置为“No”时,FLUSPECT只生成光谱,不生成荧光材质,可等同于PROSPECT。
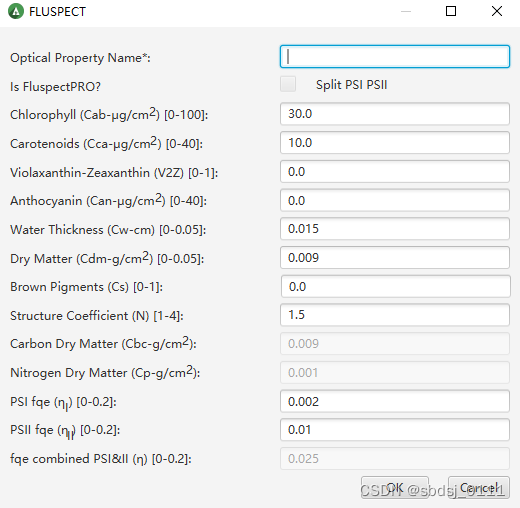
LESS目前只模拟了叶片荧光发射后,在冠层中的辐射传输过程,无法精确刻画环境,如光照、温度等对叶片荧光产量的影响。用户可通过为object分组,赋予不同的叶片参数,即不同的FLUSECT输入参数,来近似描述环境的影响。
荧光产品存放在Results目录下,并带有“Fluor”标记。各荧光产品的介绍如下表。

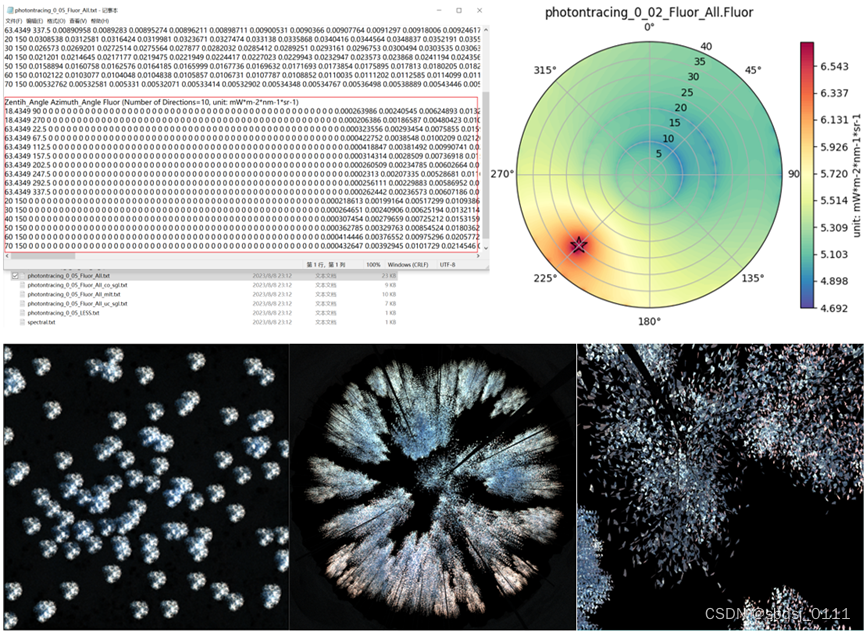
Vilfan N, Van Der Tol C, Muller O, Rascher U and Verhoef W. 2016. Fluspect-B: A model for leaf fluorescence, reflectance and transmittance spectra. Remote Sensing of Environment, 186: 596-615 [DOI: 10.1016/j.rse.2016.09.017] ↩︎
Vilfan N, Van Der Tol C, Yang P, Wyber R, Malenovský Z, Robinson S A and Verhoef W. 2018. Extending Fluspect to simulate xanthophyll driven leaf reflectance dynamics. Remote Sensing of Environment, 211: 345-356 [DOI: 10.1016/j.rse.2018.04.012] ↩︎
egaieg O, Lauret N, Wang Y, Guilleux J, Chavanon E and Gastellu-Etchegorry J-P. 2023. Bi-directional Monte-Carlo modelling of solar-induced chlorophyll fluorescence images for 3D vegetation canopies in the DART model. International Journal of Applied Earth Observation and Geoinformation, 118: [DOI: 10.1016/j.jag.2023.103254] ↩︎