全文链接:https://tecdat.cn/?p=33742
在选择最佳拟合实验数据的方程时,可能需要一些经验。当我们没有文献信息时该怎么办?我们建立模型的方法通常是经验主义的。也就是说,我们观察过程,绘制数据并注意到它们遵循一定的模式(点击文末“阅读原文”获取完整代码数据)。
相关视频
简介
例如,我们的客户可能观察到一种植物对某种毒性物质的反应是S形的。因此,我们需要一个S形函数来拟合我们的数据,但是,我们如何选择正确的方程呢?
我认为列出最常见的方程以及它们的主要特性和参数的意义可能会有用。因此,我还将给出相应的R函数。
非线性回归的一个问题是它以迭代方式工作:我们需要提供模型参数的初始猜测值,算法逐步调整这些值,直到(有希望)收敛到近似最小二乘解。根据我的经验,提供初始猜测可能会很麻烦。因此,使用包含R函数非常方便,这可以极大地简化拟合过程。
让我们加载必要的包。
library(nlme)曲线形状
曲线可以根据其形状进行简单分类,这对于选择正确的曲线来研究过程非常有帮助。我们有:
多项式
线性方程
二次多项式
凹/凸曲线(无拐点)
指数方程
渐近方程
负指数方程
幂曲线方程
对数方程
矩形双曲线
Sigmoid 曲线
逻辑方程
Gompertz 方程
对数-逻辑方程(Hill 方程)
Weibull 类型 1
Weibull 类型 2
具有最大值的曲线
Brain-Cousens 方程
多项式
多项式是描述生物过程的最灵活的工具。它们简单,并且虽然是曲线状的,但它们在参数上是线性的,并且可以通过使用线性回归来拟合。一个缺点是它们不能描述渐近过程,而这在生物学中非常常见。此外,它们容易过度拟合,因为我们可能会试图添加项来改善拟合,而很少关心生物现实性。
线性方程
显然,这不是一条曲线,尽管值得在这里提到。方程为:
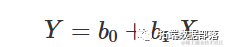
其中 b0 是当 X = 0 时 Y 的值,b1 是斜率,即 X 增加/减少一个单位时 Y 的增加/减少。当 b1>0 时,Y 随着 X 的增加而增加,否则随之减少。
二次方程
该方程为:
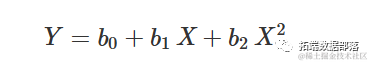
其中,当 X=0 时, b0 是 Y 的值,当 X=0 时, b1和 b2 各自没有明确的生物学意义。然而,考虑到一阶导数为:
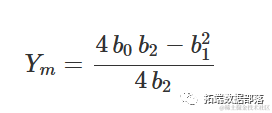
它测量了在 X 增加一个单位时 Y 的增加/减少。我们可以看到这种增加/减少不是恒定的,而是根据 X 的水平而变化。
在最大值/最小值处,响应为:
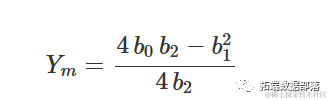
R 中的多项式拟合
在 R 中,可以使用线性模型函数 'lm()' 进行多项式拟合。虽然这不是高效的方法,但在某些情况下,我发现自己需要使用 'nls()' 或 'drm()' 函数进行多项式拟合。
凹/凸曲线
让我们进入非线性领域。凹/凸曲线描述了非线性关系,通常带有渐近线和无拐点。我们将列出以下最常用的曲线类型。
指数方程
指数方程描述了递增/递减的趋势,具有恒定的相对速率。最常见的参数化形式是:
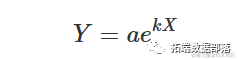
其他可能的参数化形式包括:
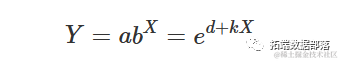
上述参数化形式是等价的,可以通过设置
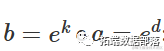
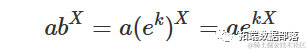
以及
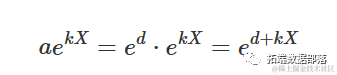
参数的含义很明确:当 X=0 时, a 是 Y 的值,而 k 表示 X 增加一个单位对 Y 的相对增加/减少。如果我们计算指数函数的一阶导数:
D( expression(a * exp(k * X)), "X")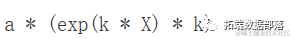
从上面我们可以得出结论:通过 X 绘制的切线的斜率为 k,也就是 (k, Y)。因此,Y 增加的量与其实际水平成比例。
moel <- drm(Cnc ~ ime fc = DRC.pDcay(),
daa =eradtion)
sumay(mdel)
plt(mdel, log="")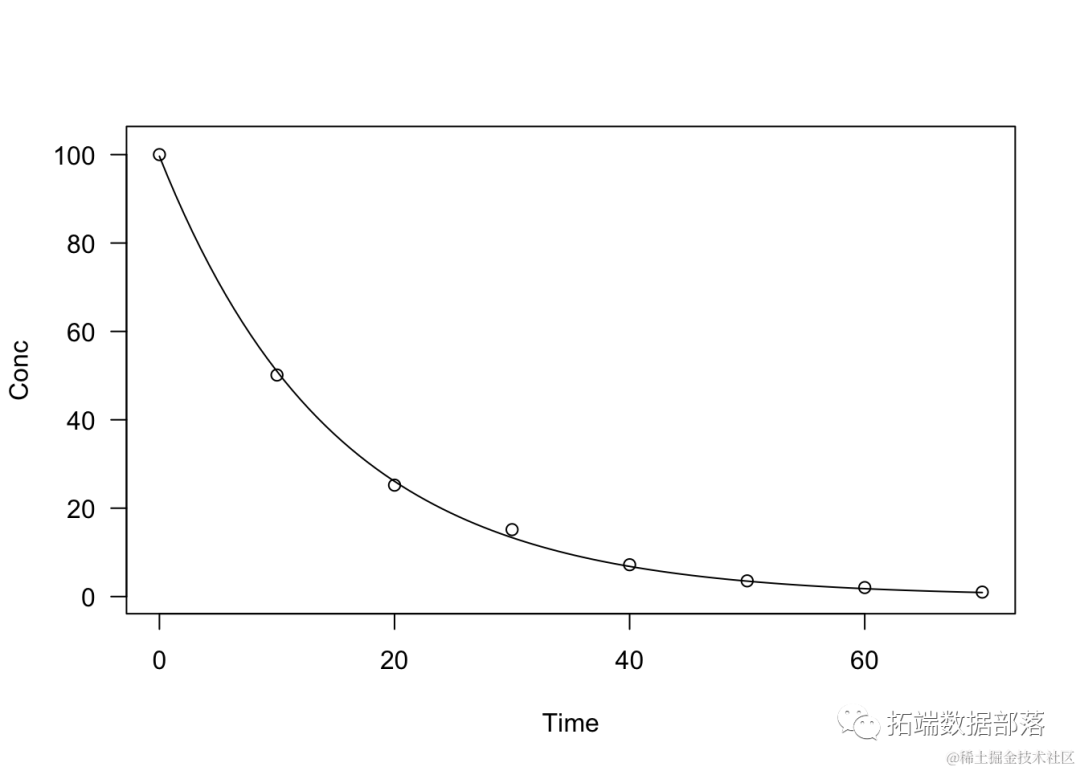
'drc' 包还包含 'EXD.2()' 函数,它拟合了一个稍微不同参数化的指数衰减模型:
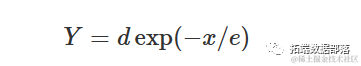
其中,d与上述模型中的a相同,e=1/k。
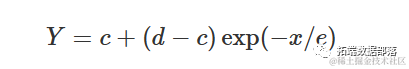
我将同时展示EXD.2(蓝色曲线)和EXD.3(红色曲线)的示例。
R
curve(EXD.fun(x, 0, 100, -1/0.05), col="blue", xlab = "X",
ylab = "Y", main = "指数衰减",
xlim = c(0, 100), ylim = c(0,100))
curve(EXD.fun(x, 20, 100, -1/0.05), col="red", add = T)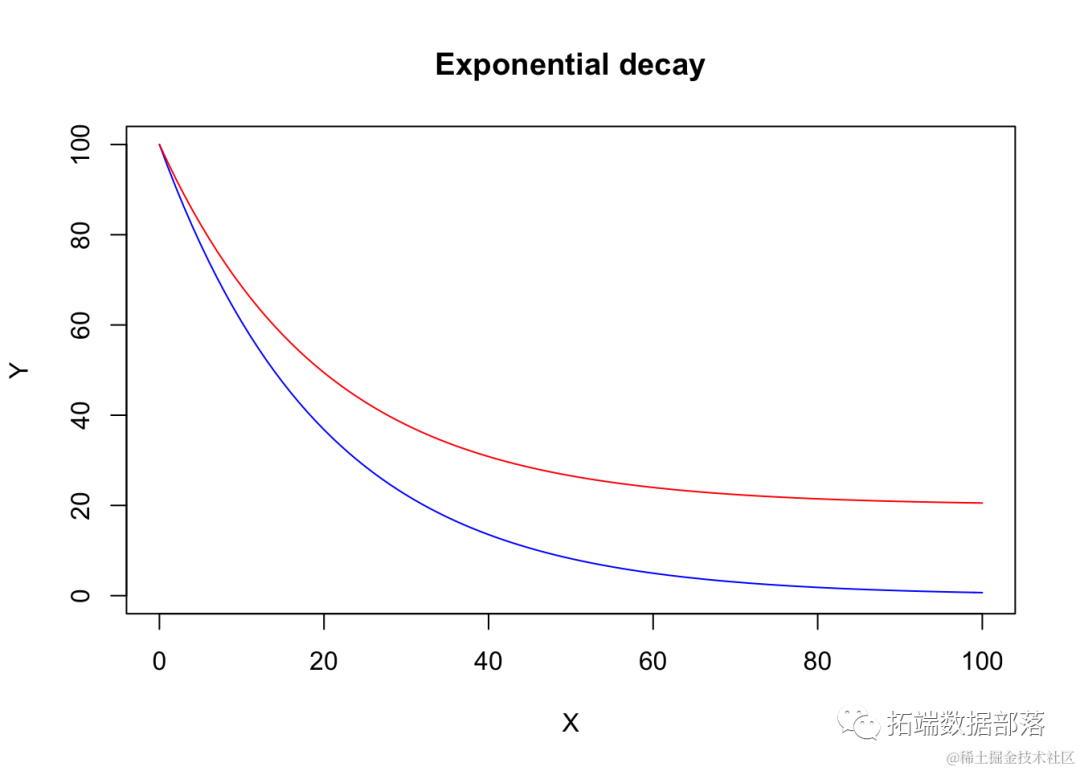
点击标题查阅往期内容

R语言nlme、nlmer、lme4用(非)线性混合模型non-linear mixed model分析藻类数据实例

左右滑动查看更多

01
02
03
04
渐近回归模型
渐近回归模型描述了有限增长,其中当X趋于无穷大时,Y趋近于一个水平渐近线。这个方程有多种不同的参数化形式,也被称为单分子生长、Mitscherlich定律或von Bertalanffy定律。
由于其生物学意义,最常见的参数化形式是:
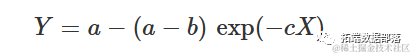
其中a是最大可达到的Y,b是x=0时Y的值为0,c与Y随X增加而相对速率成比例。事实上,我们可以看出它的一阶导数是:
R
D(exesion(a - (a - b) * exp (- c * X)), "X")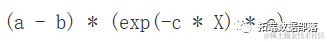
即:
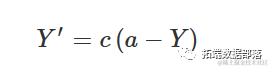
我们可以看到生长的相对速率并不是常数(如指数模型中),而是在Y=0时最大,并随着Y的增加而减小。
让我们模拟一个示例。
R
model <- rmY ~ X, fct = DC.syReg())
plot(odl, log="", main = "渐近回归")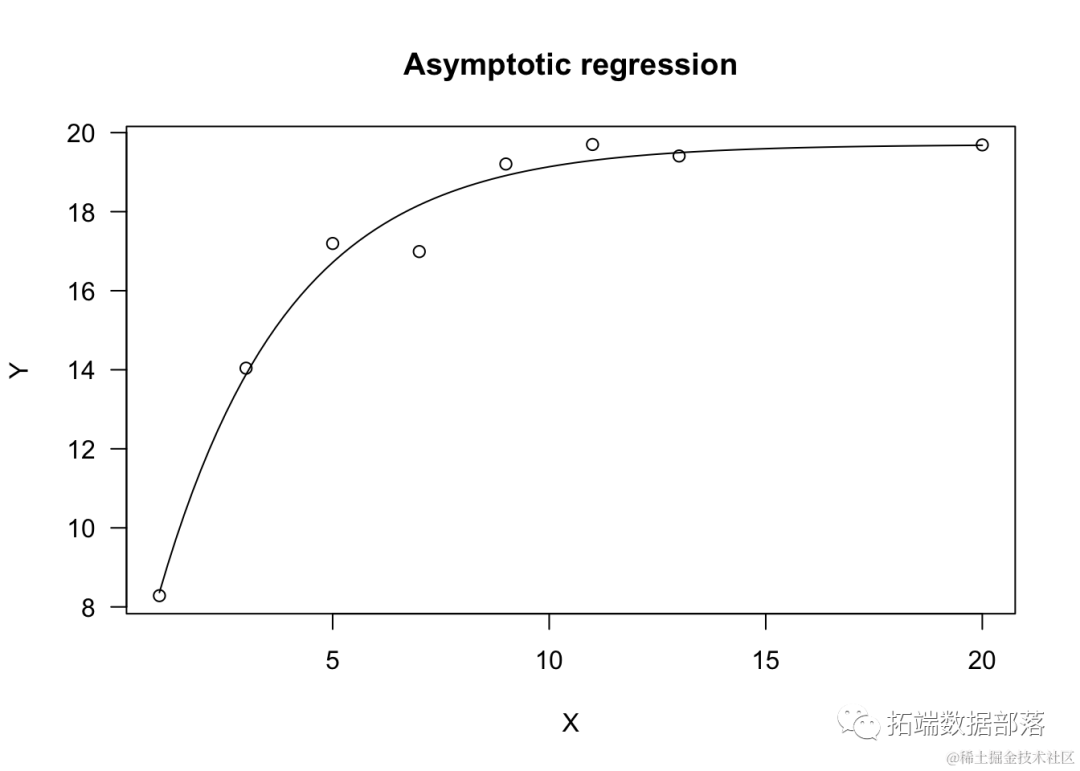
负指数方程
如果我们在上述方程中加上限制条件b=0,我们得到以下方程,通常被称为“负指数方程”:
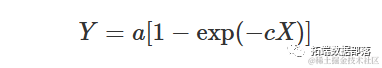
这个方程的形状与渐近回归类似,但当X=0时,Y=0(曲线通过原点)。它通常用于建模吸收的光合有效辐射(Y=PARa)与入射光合有效辐射(a=PARi)、叶面积指数(X=LAI)和消光系数(c=k)之间的关系。
幂函数曲线
幂函数曲线也被称为弗洛伊德方程或者等比方程,最常用的参数化形式如下:
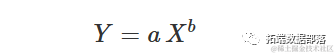
这个曲线与X的对数上的指数曲线等效,实际上可以表示为:
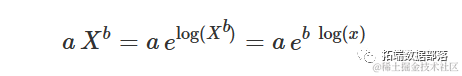
对于X→∞,曲线并没有渐近线。斜率(一阶导数)为:
D(expression(a * X^b), "X")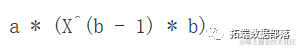
我们可以看到两个参数与曲线的斜率有关,b决定了曲线的形状。当0<−b<1时,随着X的增加,Y也会增加,曲线呈现凸向上的形状。例如,这个模型可以用于根据采样面积来建模植物物种数量(Muller-Dumbois方法)。
moel <- drm(nuSces ~ Aea, fct = DCowCurve(),
data = spieAra)
summary(mdel)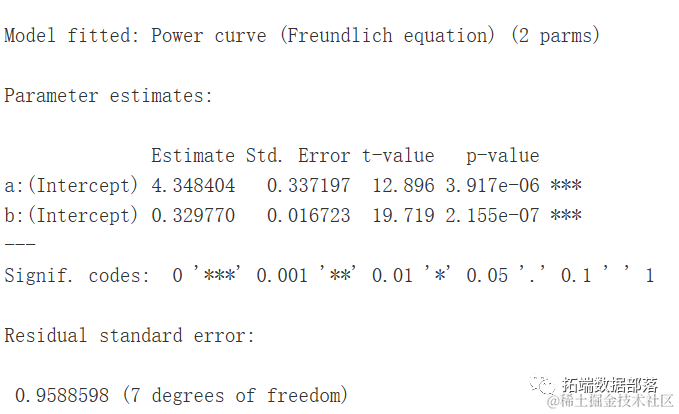
plot(oel, log="")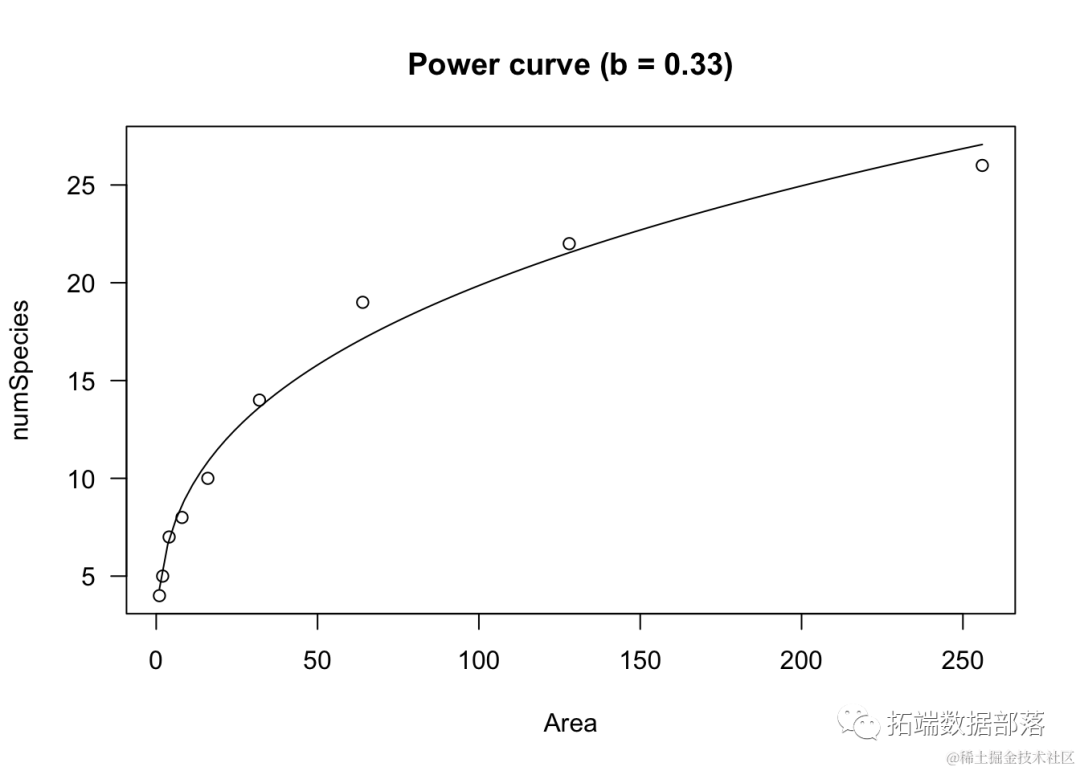
如果b<0,曲线将呈现凹向上的形状,Y随着X的增加而减少。
curve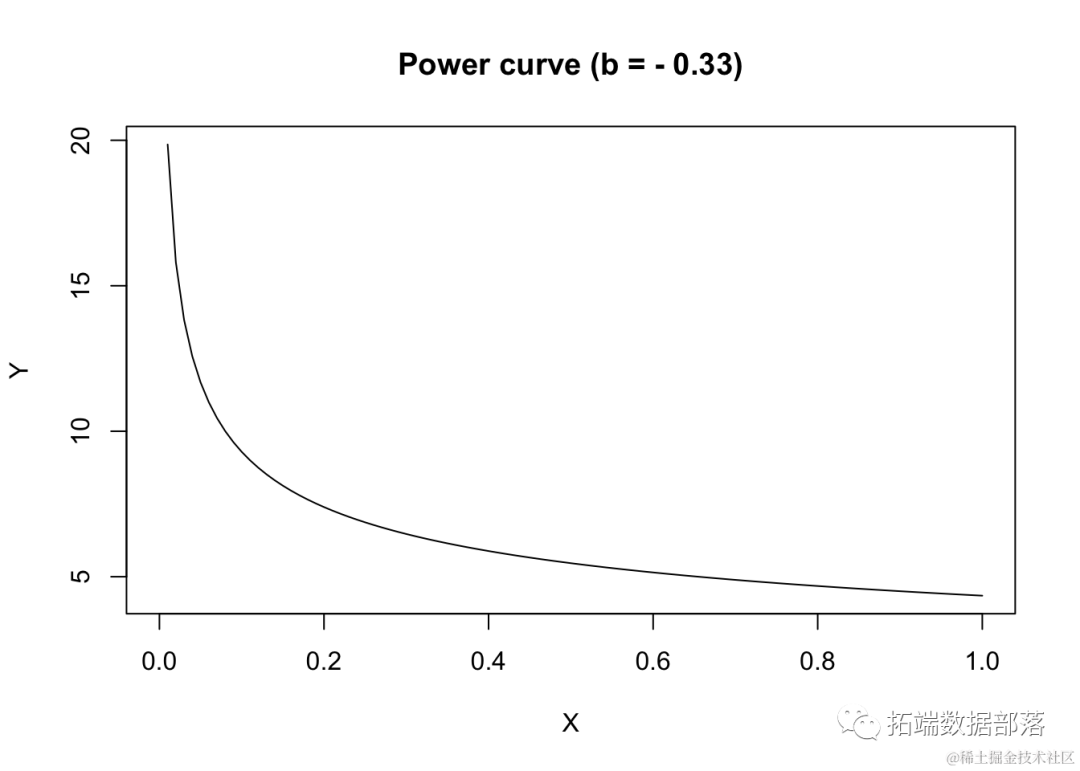
如果b>1且为负数,曲线将呈现凹向上的形状,Y随着X的增加而增加。
curve(powerC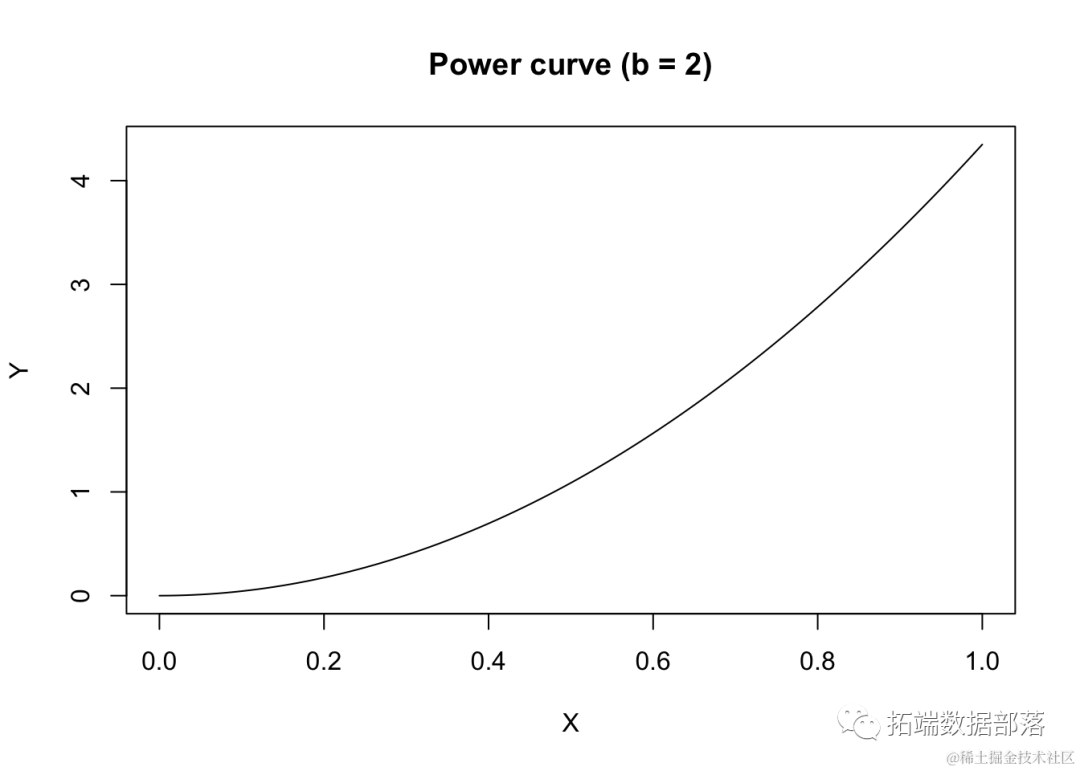
对数方程
这确实是一个对数转化后的线性模型:
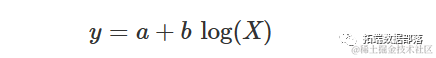
可以使用 'lm()' 函数来拟合对数方程。
# b 是正值
model <- lm(Y ~ log(X) )
summary(model)
summary(model)
plot(model,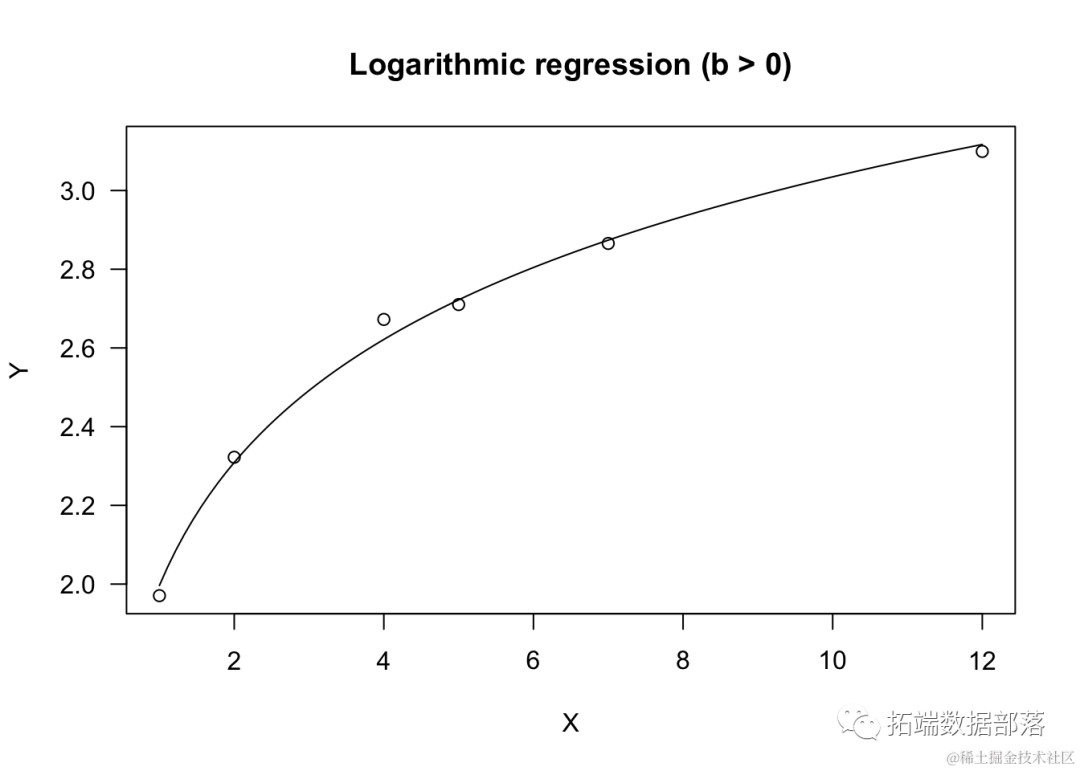
# b 是负值
X <- c(1,2,4,5,7,12)
a <- 2; b <- -0.5
summary(model)
plot(model, log="",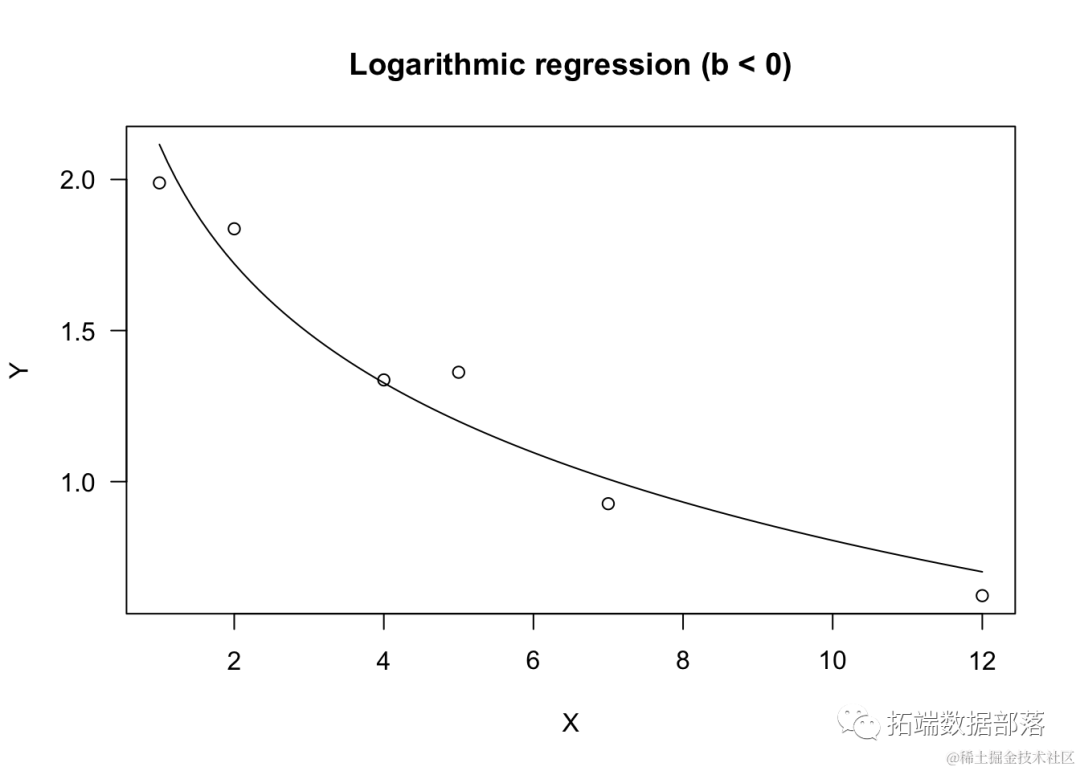
Michaelis-Menten方程
这是一个双曲线形状的方程,通常参数化为:
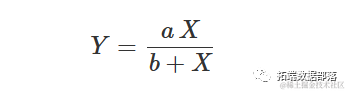
这条曲线朝上凸起,随着X′ 的增加而增加,直到达到一个平台水平。参数a′ 表示高位渐近线(对于X→∞),而b′ 是使得响应等于a/2的X值。事实上,很容易证明:
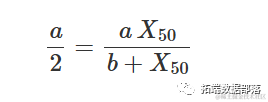
由此可得,b=x50=50。
斜率(一阶导数)为:
D(expression( (a*X) / (b + X) ), "X")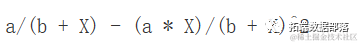
从这里可以看出,初始斜率(在X=0时)为 i=a/b。
{r}
res <- rnorm(8, 0, 0.1)
Y <- Ye + res
# nls拟合
mol <- nls(Y ~ SSien(X, a, b))
summary(model)
{r}
# drm拟合
summary(model)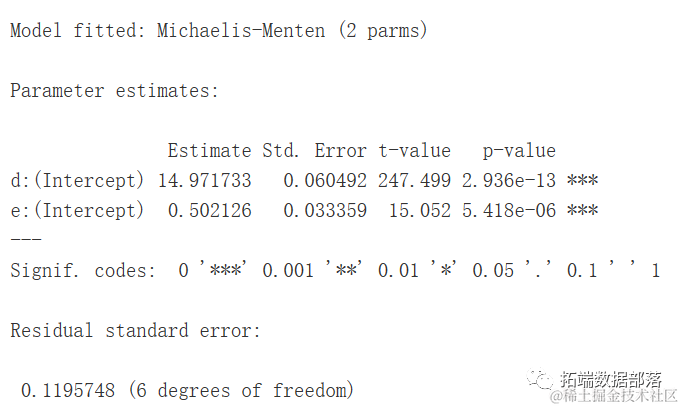
{r}
plot(model, log="", main = "Mic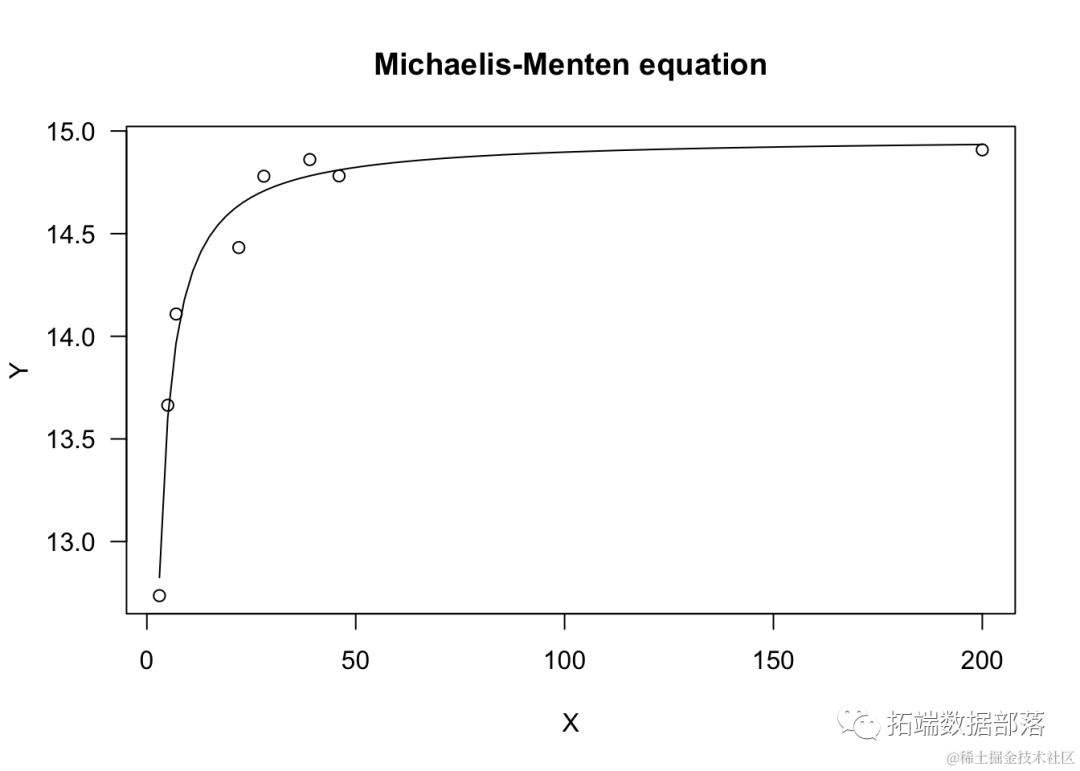
"drc"包还包含自启动函数 "MM.3()",其中当 X=0 时,允许 Y ≠ c ≠ 0。
产量损失/密度曲线
杂草与农作物竞争研究使用重新参数化的Michaelis-Menten模型。实际上,Michaelis-Menten的初始斜率可以被视为竞争的测量,即在首次添加杂草到系统中时产量(Y)的减少。因此,将Michaelis-Methen模型重新参数化以将i=a/b=α/β作为显式参数进行描述。重新参数化的方程为:
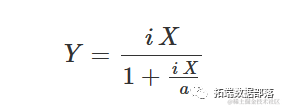
该模型可用于描述杂草密度对产量损失的影响。因此需要使用无杂草的产量和以下方程来计算产量损失(百分比):
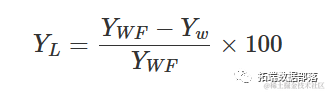
其中,YW是观测到的产量,YWF是无杂草的产量。下面以日葵种植在增加密度的Sinapis arvensis杂草中的情况为例进行说明。
{r}
competition$YL <- (Ywf - competition$Yield) / Ywf * 100
# nls拟合
summary(model)
{r}
# drm拟合
summary(model)
{r}
plot(model, log="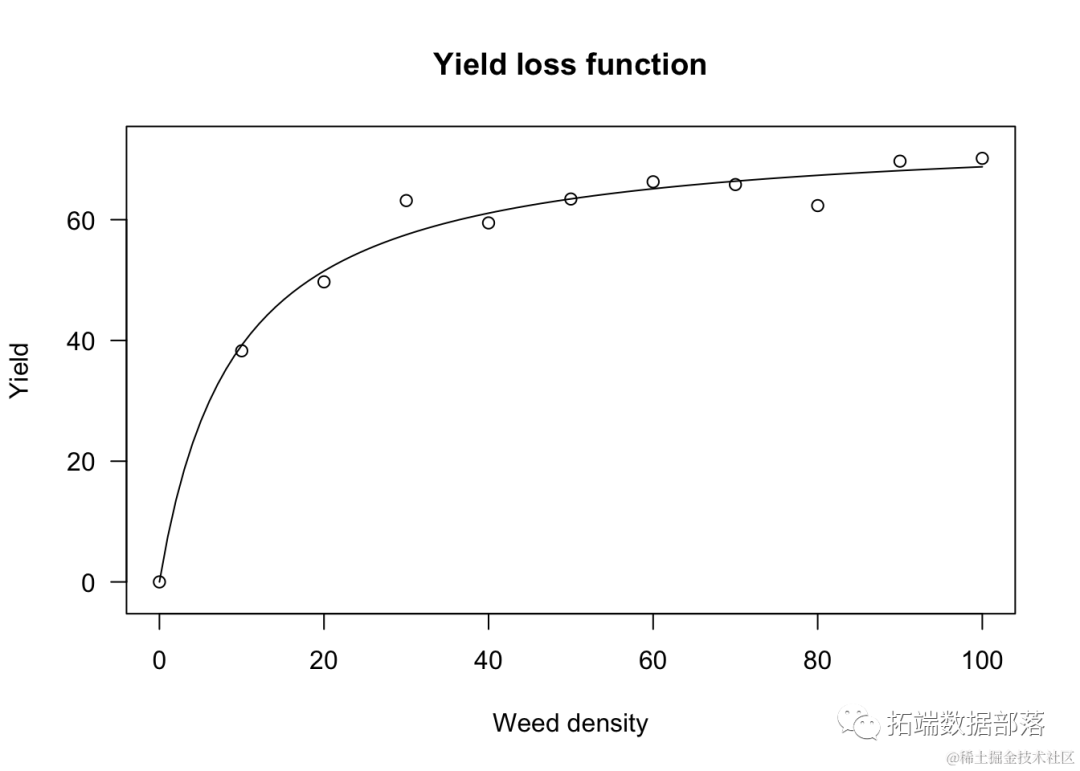
上述拟合约束了当杂草密度为0时,产量损失为0。
确实,从上述方程我们推导出:
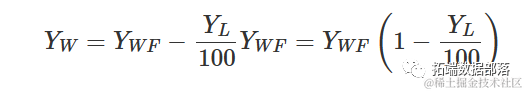
和所示:
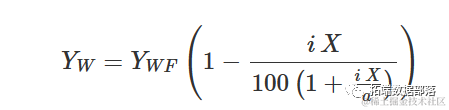
model <- dr
summary(model)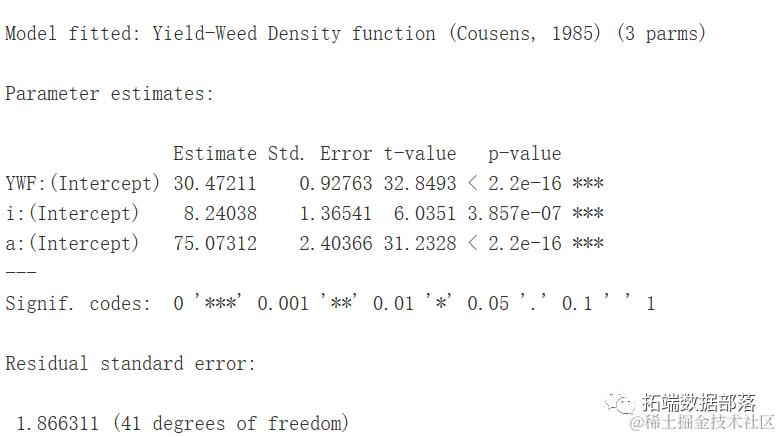
plot(model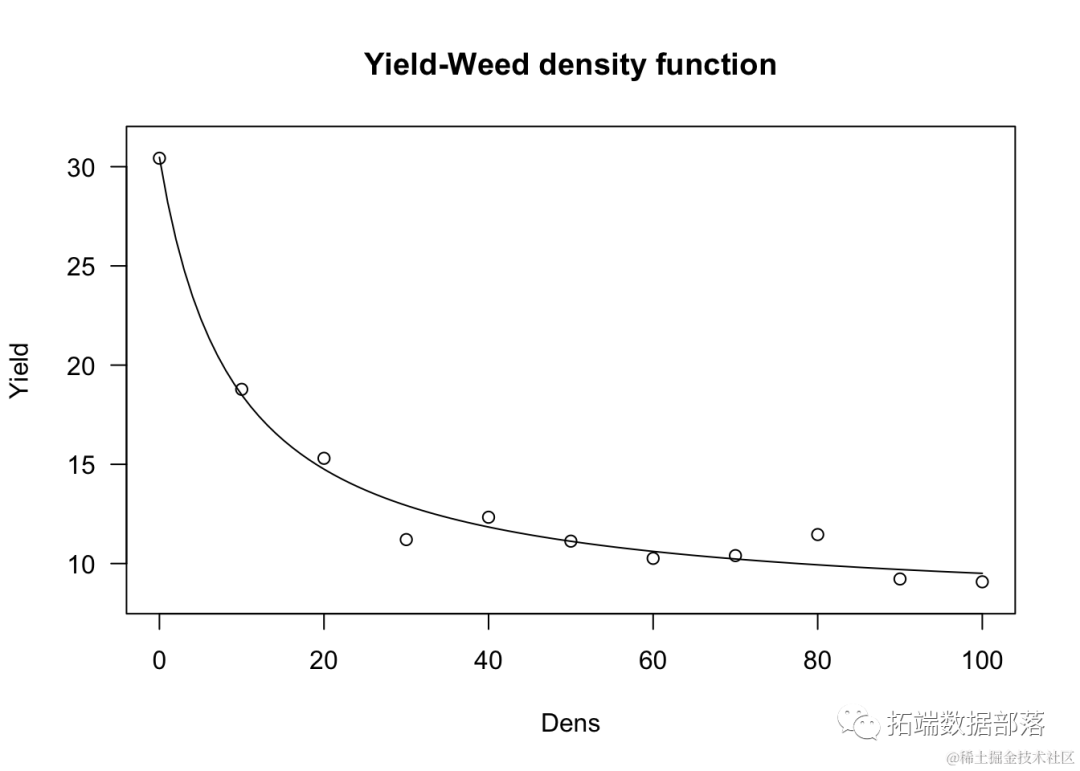
S 型曲线
S 型曲线具有 S 形状,可以是递增、递减、对称或非对称的。它们有许多参数化方法,有时可能让人困惑。因此,我们将展示一种常见的参数化方法,这在生物学方面非常有用。
逻辑曲线
逻辑曲线来源于累积逻辑分布函数;曲线在拐点处对称,并可以参数化为:
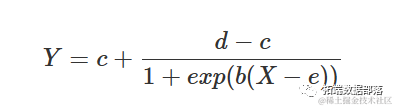
其中,d 是上渐近线,c 是下渐近线,e 是在 d 和 c 之间产生响应的 X 值,而 b 是拐点附近的斜率。参数 b 可以是正数或负数,因此 Y 可以随着 X 的增加而增加或减少。
逻辑函数非常有用,例如用于植物生长研究。
model <- dm(weightFree ~ DAE, fct =
sum
plot(model, log="",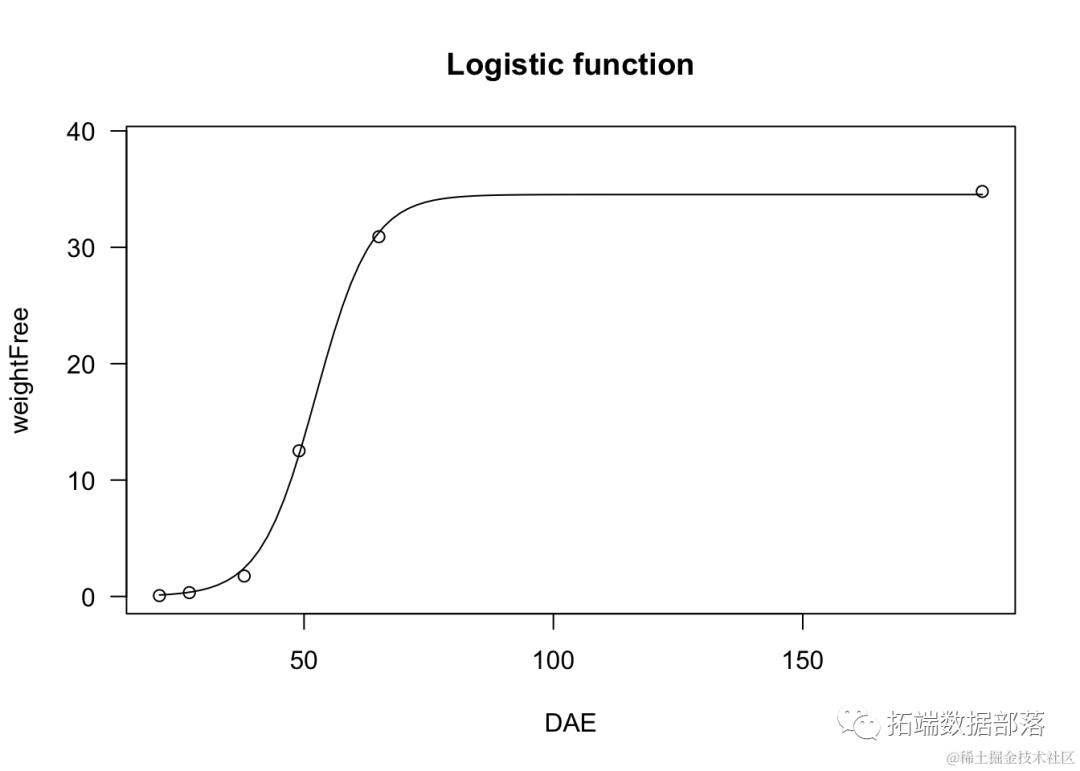
Gompertz 曲线
Gompertz 曲线有许多参数化方法。我们倾向于使用与逻辑函数相似的参数化方法:
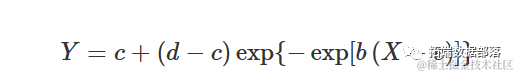
其中参数的含义与逻辑函数中的参数相同。不同之处在于该曲线在拐点处不对称。
另一种不对称性
我们已经看到,相对于逻辑函数,Gompertz 函数在开始时呈现更长的延迟,但之后稳步上升。我们可以通过以下方式更改 Gompertz 函数来描述不同的模式:
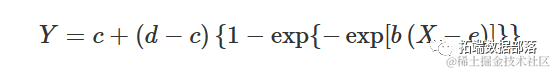
该函数的自启动函数尚不可用,至少在我所知道的范围内。此外,我也不知道这个函数的特定名称。
通过在图表中比较这三个逻辑函数,我们可以看到它们在偏斜和对称性方面的差异。
curve( E.fun(x, b, c, d, e), add = T, col = "blue" )
legen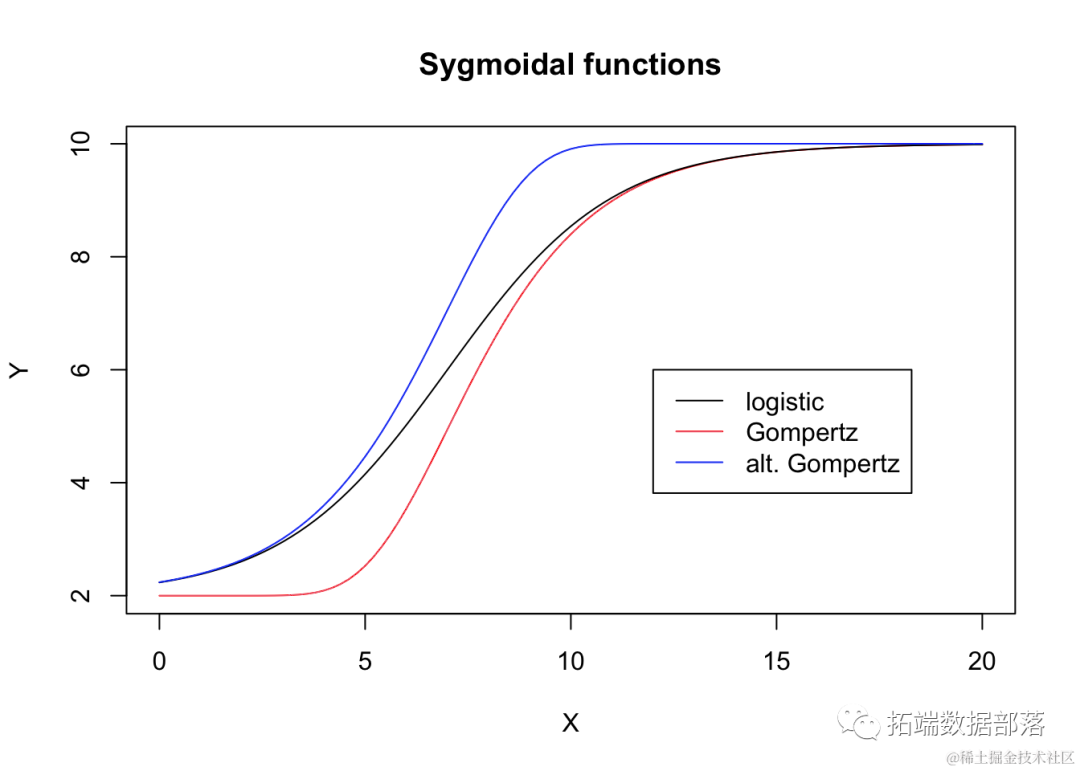
基于对数的 S 型曲线
在生物学中,测量的数值通常是严格为正的(时间、重量、高度、计数)。因此,使用对非正数也定义的函数可能看起来不现实。因此,通常更倾向于使用独立变量 X 被限制为正的函数。所有上述描述的 S 型曲线都可以基于 X 的对数进行,这样我们可以得到更现实的模型。
对数-逻辑曲线
在许多应用中,S 型响应曲线在 x 的对数上是对称的,这需要一个对数-逻辑曲线(对数正态曲线实际上几乎等效,但很少使用)。例如,在生物测定中(但也在萌发测定中),对数-逻辑曲线定义如下:
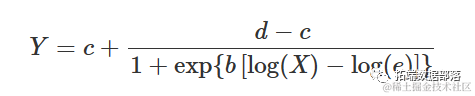
参数的含义与上述逻辑方程中的含义相同。很容易看出上述方程等价于:
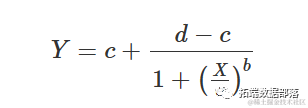
另一种可能的参数化方法是所谓的 Hill 函数:
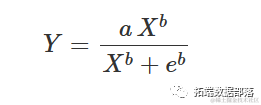
确实:
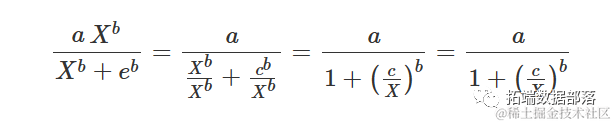
对数-逻辑函数用于作物生长、种子萌发和生物测定,它们可以具有与逻辑函数相同的约束条件。
我们展示了一个基于对数-逻辑拟合的示例,涉及到对一个除草剂处理的甘蓝菜生物测定中不断增加剂量的关系。
dm(FW~ Dose,fct = L.4(),data =brssica)
summary(model)
plot(model, main = "对数-逻辑方程")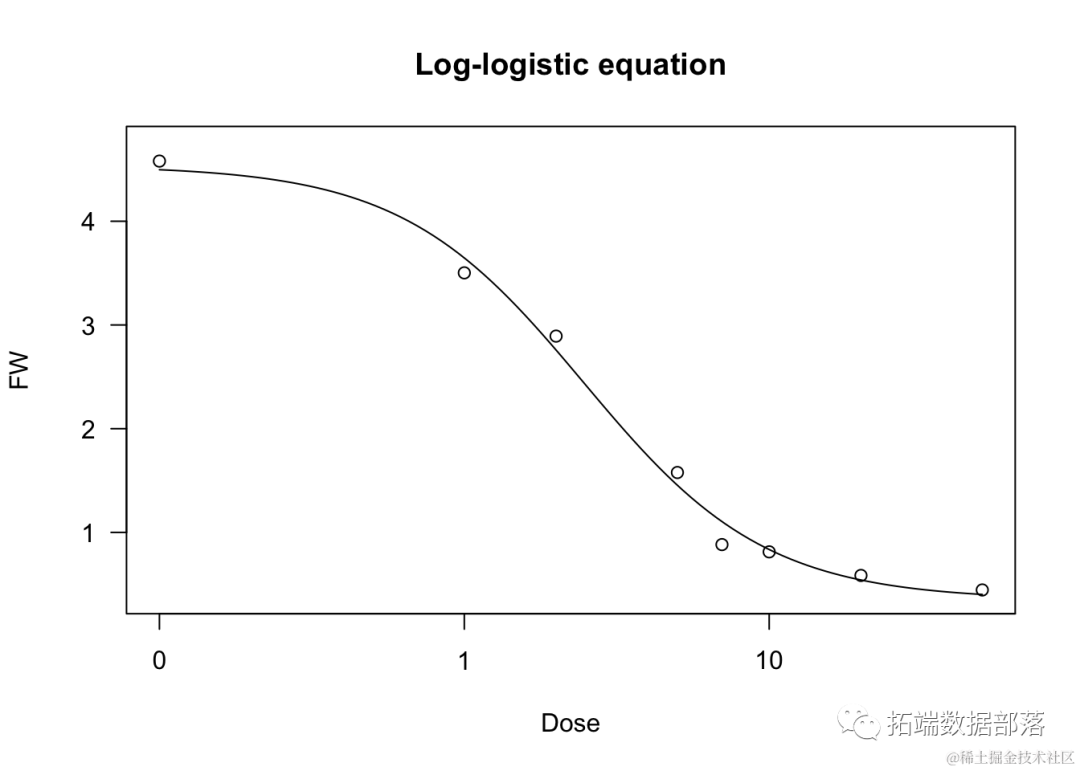
Weibull 曲线(类型 1)
类型 1 Weibull 曲线与替代 Gompertz 曲线的对数-逻辑曲线相似。方程如下:
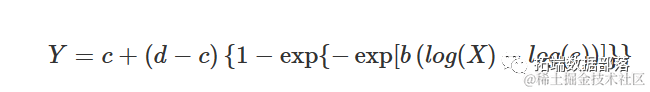
参数与上述其他 S 型曲线的含义相同。
Weibull 曲线(类型 2)
类型 2 Weibull 曲线与 Gompertz 曲线的对数-逻辑曲线相似。方程如下:
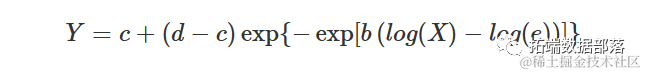
参数与上述其他 S 型曲线的含义相同。
我们将对这些 Weibull 曲线拟合数据集。
plot(model, main = "Weibull functions")
plo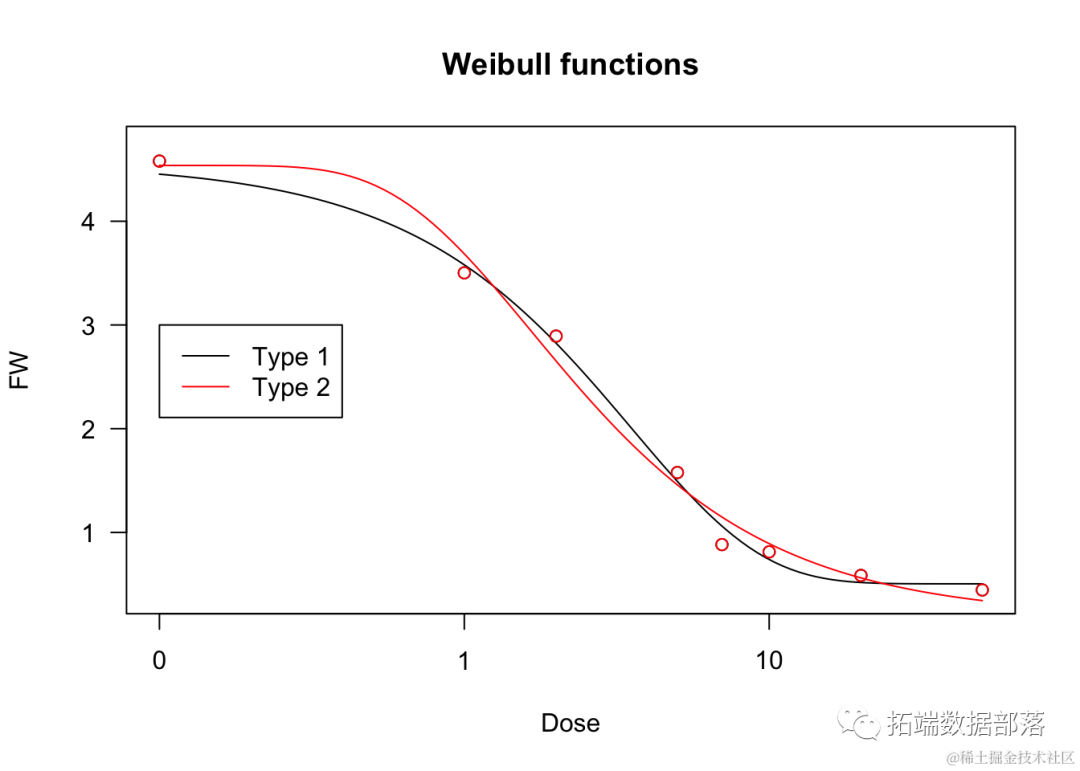

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言非线性方程数值分析生物降解、植物生长数据:多项式、渐近回归、米氏方程、逻辑曲线、Gompertz、Weibull曲线》。


点击标题查阅往期内容
R语言混合线性模型、多层次模型、回归模型分析学生平均成绩GPA和可视化
R语言线性混合效应模型(固定效应&随机效应)和交互可视化3案例
R语言用lme4多层次(混合效应)广义线性模型(GLM),逻辑回归分析教育留级调查数据
R语言 线性混合效应模型实战案例
R语言混合效应逻辑回归(mixed effects logistic)模型分析肺癌数据
R语言如何用潜类别混合效应模型(LCMM)分析抑郁症状
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言建立和可视化混合效应模型mixed effect model
R语言LME4混合效应模型研究教师的受欢迎程度
R语言 线性混合效应模型实战案例
R语言用Rshiny探索lme4广义线性混合模型(GLMM)和线性混合模型(LMM)
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言如何解决线性混合模型中畸形拟合(Singular fit)的问题
基于R语言的lmer混合线性回归模型
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
R语言分层线性模型案例
R语言用WinBUGS 软件对学术能力测验(SAT)建立分层模型
使用SAS,Stata,HLM,R,SPSS和Mplus的分层线性模型HLM
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
SPSS中的多层(等级)线性模型Multilevel linear models研究整容手术数据
用SPSS估计HLM多层(层次)线性模型模型

![]()