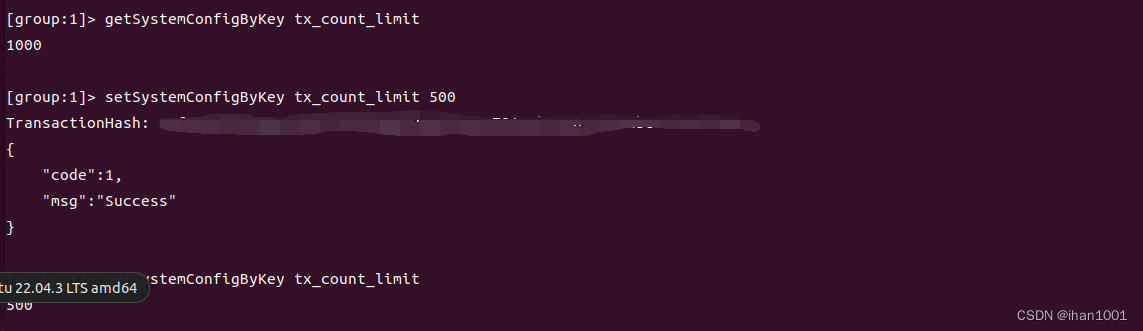
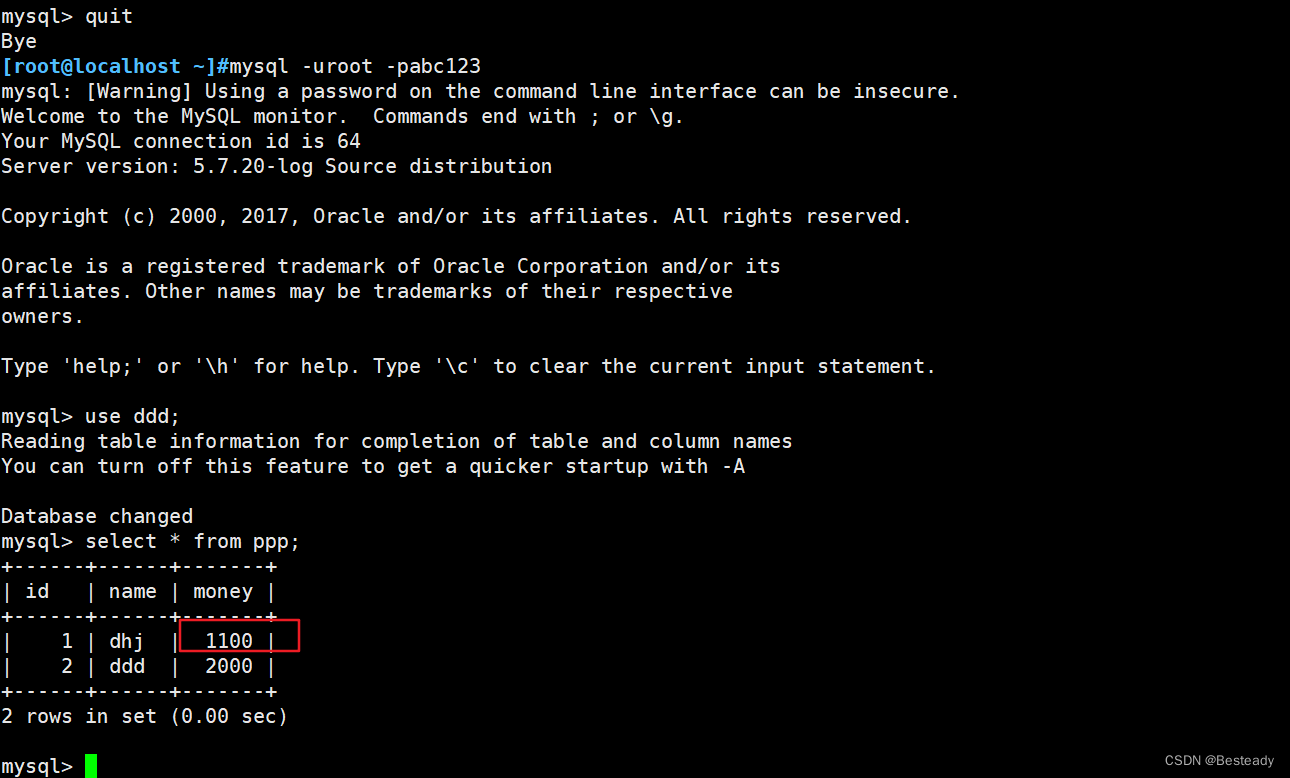
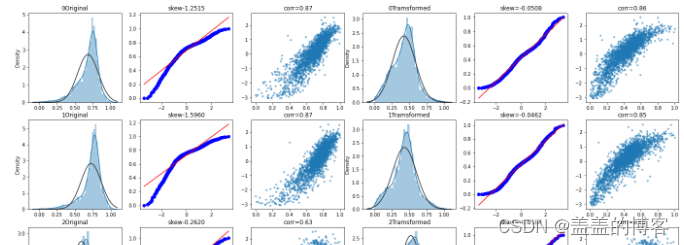
小数转二进制



小数部分呈6,2,4,8循环,则二进制序列为1001循环
小数点前的0应该没有任何用,就是表示这是个小数,第一位转化后如果是1,应该是在小数点后的第一位位置
原始小数(通过机制)——无限二进制序列——(逆过程)还原小数
对于逆过程,第2位为1,则2^2=4,取倒数与1乘,第5位为1,2^5=32,取倒数与1乘
精度越高,二进制序列存储长度越长,还原效果越好
二进制乘法

浮点数构造
浮点数64位,一位是符号位,11位是指数位,52位mantissa(尾数)
分别是啥?

科学计数法的指数位就是10的多少次幂

对于3,转为二进制为11,超过了1位(当前进制数),有一个2
二进制乘法和十进制不一样
十进制中小数点移动伴随着乘十或除十,二进制中小数点移动伴随着乘二除二,1.1x2^1,有乘2,就让小数点往前移,即(11)2,为(3)10.
小数点往前移几位,就表明当前进制的规模(指数位)是多大
101.0要往前移2位,则指数位就是2
二进制里的个还是那个个的意思吗?
是。(1.1)2个2,(1.1)2不是(1.1)10。十进制尾数进指数,就是小数点往前移一位,需要的是尾数大于进制
如果是二进制,就是说小数点前的数只能保持1位,小数点每往前移一位,就意味着除了一个2,就是当前指数规模扩大了一点。

8位指数位,2^8=256=128^2,加127就是说,把负数映射到0~127,把正数映射到128~256
+127就是指数位第7位上加1
尾数真值=1+存储的尾数(即小数点后的部分)



浮点数精度和范围
 1.111111……=1+0.5+0.25+0.125……
1.111111……=1+0.5+0.25+0.125……
尾数
(比如11,就是超过了10(当前进制数),就需要把这个10移到指数上(指数位的大小表示当前数的规模),尾数在10以内就表示当前这个数在当下这个规模的进制数还能表示,一旦尾数超过了10,就说明这个数在当下这个规模的进制数就不能表示了,这个数即超过了当前指数记录规模的最大范围,此时就需要指数位++,直到能用一个比进制小的尾数来表示这个数,也就更新好了进制数的范围)
(如111,就不能用10^1表示,因为超出了10^1所能表示的范围,需要10^2的规模才能表示这个数)
小数点就是小数点,不会因为进制的改变而改变含义,只是小数点前面的数(那么多的数)用哪种进制表示而已,如果用十进制就是3,二进制就是11
十进制的表示法,指数的底数就是10,二进制的底数,就是2
怎么理解?
科学计数法应该就是说,由多少组的10(一个进制)构成,拆出两部分就是具体是多少,一个小于进制的数,即尾数,用于精确到底是多少,一个当前进制的指数(即只能由进制组成,指数表示当前进制表示的规模(指数越大,规模越大,表示范围越大),多于进制的取模使进制的数量增加,并使多余部分进入尾数,少于的直接进入尾数)。
![]()
指数部分决定数的大小范围,有效数字
同样的数,指数越大,则用来表示的尾数越小,因为当前指数越大,规模越大,那么就不需要用很多当前这个规模的进制数;而如果指数越小,进制部分的规模就越小,尾数越大,表示需要多用当前小规模的进制组才能表示出这个数
而由于尾数部分不会超过进制,所以数的大小都由指数部分确定,即如果指数最大n位,则只能表示到当前进制^n^尾数最大(即当前进制数),再大就表示不了
二进制计数法,就是要尾数不大于2(当前进制数),尾数是小数,表示具体由多少个当前指数规模的2组成,

由尾数M和阶码E构成

阶码是整数,则2^E就是整数,所以尾数M必须为小数才可以使F为小数
怎么使M为小数
MPN
什么是尾数前缀数MPN
就是给定两个双精度浮点数的尾数部分

如果两个数的尾数前半部分相同,但是有一个尾数的后部分都为0,那就把前半部分相同的位数称为尾数前缀数
尾数前缀搜索
目的是啥?
应该是为了确定到底是那部分尾数相同,就是说确定尾随0的数量
定理一(theorem)
给一个双精度的数,他的小数点后位数为α,二进制形式b,那么伊普西隆(00……。b-(f(α)……bl)就是比10^-α小,
它取得就是一个最小计数单元,它不管你用了多少个最小计数单元,就算是0.2,0.5,都是计0.1
伊普西隆是自小数点后f(α)位开始的,那伊普西隆肯定比0.f(α)小
fα是一个函数,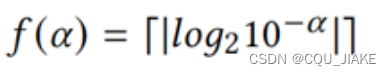 =(α*3.32193)向上取整
=(α*3.32193)向上取整
十进制α与二进制的小数点后位数并不对应
十进制中小数点后有α位,肯定并不意味着二进制小数点后有α位,如果十进制数的小数点后为α位,那么最小计数单元就是10^-α,其转为二进制就是
其在十进制中小数点后位数为α,即需要α位才能精确表示出这个数
如果转为二进制就需要 位
位
比如0.1,为10^-α,α=1,十进制中需要一位才能精确表示

log2(10)就是说由1个多大指数规模的2才能恰好组成1个10 ,要一个2^3.32193……,三位不够,如果是小数部分,那就是三位还多,
如果二进制,(向上取整),需要4位。
这个意思应该是说,转化为二进制后,0.1的表示自二进制小数点后第4位开始表示,就是说,前面的位数都没有0.1的组成部分,自第4位开始之后,开始可以组成并参与构成0.1(原十进制最小单元)
但一定有,f(α)后面的所有加起来都不比f(α)的一个大。
就是0.5>=0.25+0.125+0.0625……
1>=0.5+0.25+0.125+……
如果是0.1,就是自第四位开始组成,但是第三位为0.125,0.1<0.125,如果是0.125,那么组成结果(f(α)位后开始逼近的序列)应为0.00011111111,但是0.1不是整好的二进制数,所以α位后面不全是1,即有间隔的1,不然就有可能超过0.1,即f(α)后面的逼近序列为1100 1100

为什么定理1成立?怎么保证f(α)后面的二进制数比10^-α小?
如果算上f(α)位,应该是不能保证。第f(α)位也参与构成最小单元,而且f(α)位上必为1(即f(α)位上记录的是小于目标数的最大的一个规整二进制数,其后面所有的二进制数加起来都不比这个二进制数大(最多相等),如果这个还不用,那就必不可能凑出)
所以定理一就是说的这个事,就是知道f(α)位参与构成这个最小计数单元(就比如是0.1),后面f(α)的序列也一定有1(即不能保证自f(α)后的求和就一定不大于0.1,因为原数可能为0.2,其最小计数单元还是0.1,这个0.1还是自二进制小数点后第4位开始计数,α=4,我就不能保证在用了不同的计数单元后,f(α)位后面的序列不变,就是其后面的1是会随着具体数而变化的(这是肯定的),就比如0.125,但是我舍弃掉f(α)位,那么就算后面的都是1,也大不过这个f(α)上的数字,所以就可以保证伊普西隆是一定小于10^-α的。
对于规整的二进制小数,这么理解f(α)会出问题?不对,怎么理解
不对,不该看整体是怎么存储的,是因为0.125,最小计数单元是0.01,所以目标变成了0.01,而不是0.125这个整体
0.125组成0.125,2个0.125组成0.25,2个0.25组成0.5,在二进制中没有0.01可以用,有的只是二进制的规整的数,不能用十进制的想法,对0.17,就是有一个0.125(介于1个0.125和2个0.125之间),然后剩下的继续用二进制数凑
那么擦除就是说
擦除的结果是,从某一位开始,后面的全是0,那就是说使之成为了一个标准的二进制数
那么就是怎么确定这个某一位
如3.17,最小计数单元为0.01,转为二进制,其想法就是用什么样的二进制数去凑这个0.01,这个二进制数必须要比0.01小,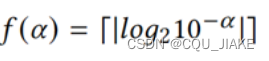
这个就是找到了首个比0.01小的二进制数的位数(小数点后),其为0.00625,比0.01小的二进制数都加起来不一定也比0.01小,如果后面都是1,就是f(α)位的二倍(少个1,即如果最低位再有个1,就会形成连续进位,直到f(α)位),即0.0125
首先,3.17里肯定有0.01,那就可以拆出3.16+0.01
自f(α)开始构成0.01,f(α)+1位的所有和<f(α)<10^(-α),
然后说把f(α)+1位及其后的所有位都置为0,只保留f(α)位,那就是说,f(α)位及其之后的数<=0.01(10^(-α)),就是近似表示了0.01,而且偏小,也就是在3.16的基础上,加了一个比0.01还小的数,但是,这样做转为二进制后就是个规整的二进制数,尾随0的数量多
可能3.16的部分也遭到了修改,但是可以保证修改的部分的和总是小于10^(-α)
再看0.125,其最小计数单元是0.001,就是0.124+0.001,那么就是把0.001给近似表示,使其从开始组成0.001的二进制位数的后一位开始都为0,也就是从那一位开始,是一个规整的二进制数
目的是,存储小数,
对任意一个十进制数(小数点后有α位)转为二进制数,小数点后保留l位(无限循环),那么构造伊普西隆为![]()
相当于还是在原十进制中取数

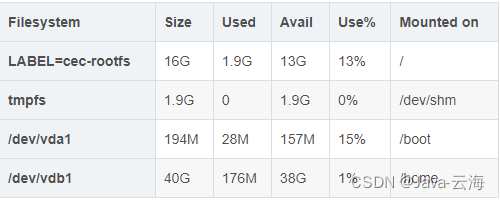
1023是啥 ,1024是二的10次方
思路是,给定一个十进制数,找到其最小存储单元






![[winerror 5] 拒绝访问。: ‘..\\data‘解决方案](https://img-blog.csdnimg.cn/ea7beb4f6e2f4703b0d67cf6ecb328f1.png#pic_center)