📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 两两交换链表中的节点
- 一般思路
- 递归思路
- 其他问题
- 删除链表的倒数第 N 个结点
- 暴力求解
- 双指针法
- 其他问题
- 环形链表 II
- 公式推导
- 相交链表
- 总结:
两两交换链表中的节点
24. 两两交换链表中的节点- 力扣(LeetCode)
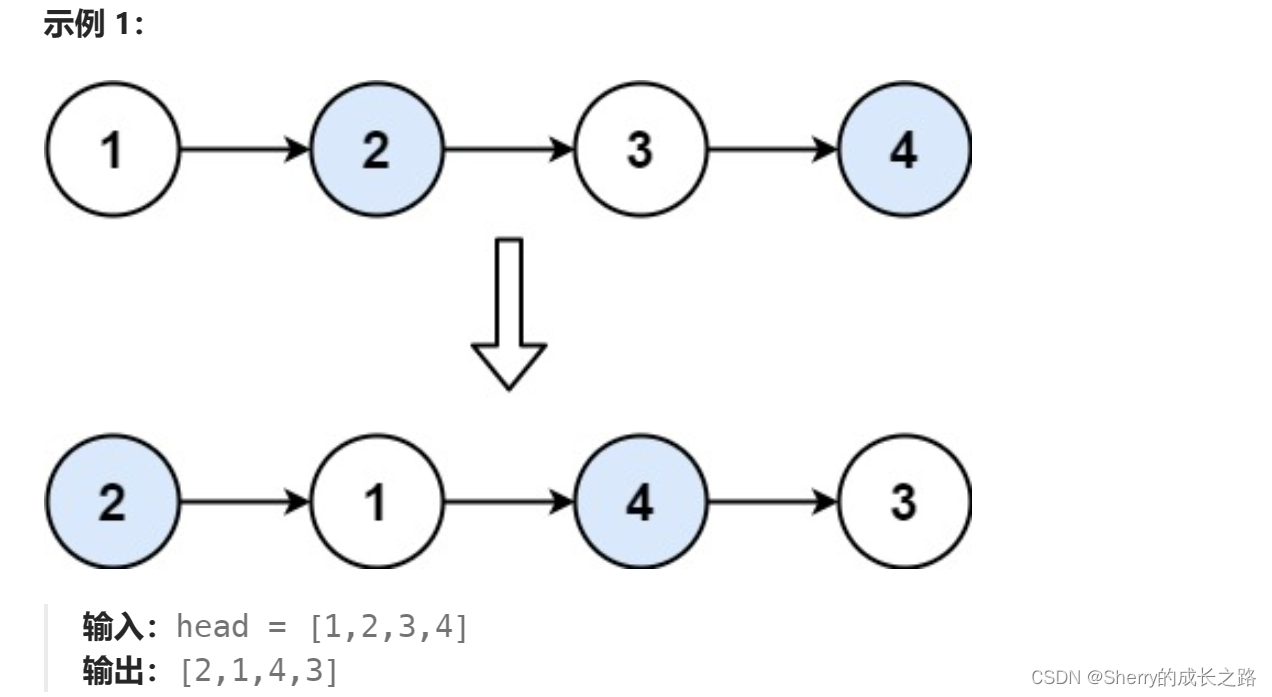
该题是交换一条链表中两两相连的节点,注意不能直接交换节点数值,而是要控制指针完成节点的交换,这道题我一听题目感觉好像是两个链表的节点互相交换的题目,但实际看到题发现并不是,看到题目有点懵,不知道该怎么交换。
这道题的要点就是要找好,交换节点哪些节点该用临时指针保存,而哪些节点并不需要保存,一定要理清思路,才不会在交换节点时候将自己绕进去。
一般思路
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr) {
ListNode* tmp = cur->next; // 记录临时节点
ListNode* tmp1 = cur->next->next->next; // 记录临时节点
cur->next = cur->next->next; // 步骤一
cur->next->next = tmp; // 步骤二
cur->next->next->next = tmp1; // 步骤三
cur = cur->next->next; // cur移动两位,准备下一轮交换
}
return dummyHead->next;
}
};
这道题也采用了虚拟头节点的技巧,交换数据时,需要找到要交换数据的上一个节点,例如题目测试用例1中,1,2节点交换信息,而1节点的上一个虚拟头节点连接的是2号节点,然后2号节点链接一号节点完成两两交换后,1节点连接之前2号节点后面的链表部分,如果没有虚拟头节点作为辅助链接,那么在第一次交换,也就是头节点需要进行两两交换时,就要单独判断一次,增加代码量的同时,也更容易出错。
上述的讲解,就已经明确了我们需要两个临时变量来指向节点,一个用来指向待交换的第一个节点,另一个用来指向第二个待交换的节点的next节点,以防交换完之后找不到后面的链表,而存储第一个待交换的节点的目的是,前一个节点链接第二个待交换的节点,后第二个节点再连第一个,方便交换。
递归思路
先两两交换后面的节点,再交换前面的节点,链接上后面交换好了的节点,注意递归结束是空节点或者只剩一个节点
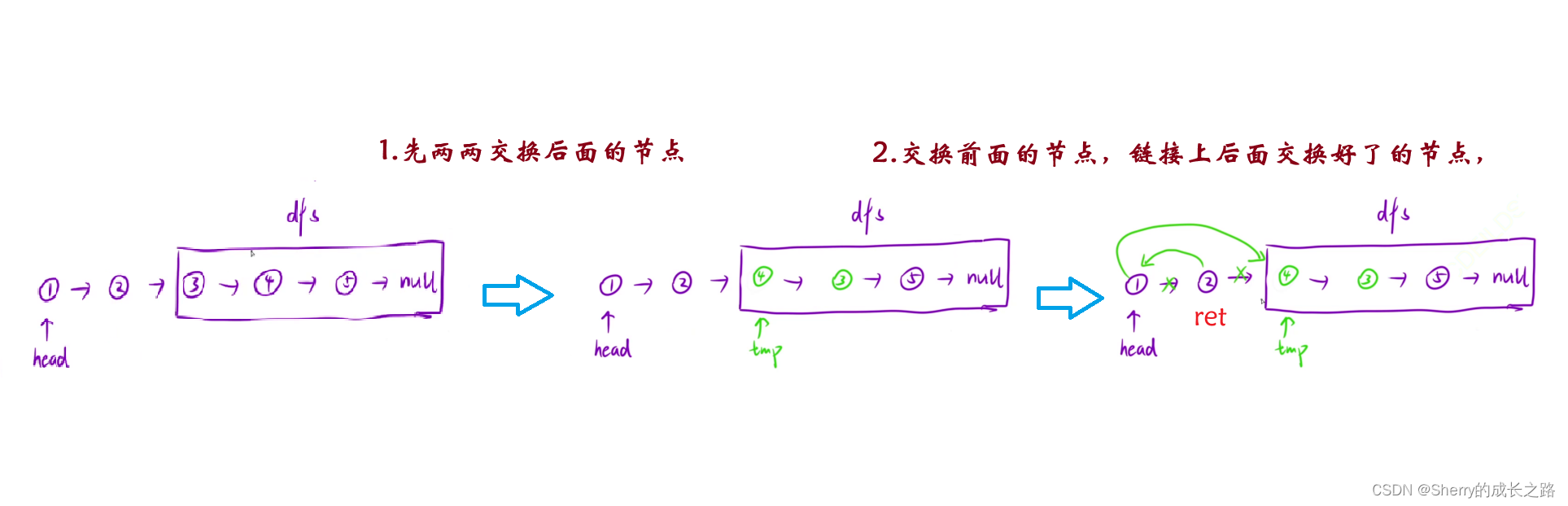
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
if(head==nullptr||head->next==nullptr)
{
return head;
}
auto tmp=swapPairs(head->head->next);//先两两交换后面的节点,返回新的头节点
auto ret=head->next;//先存一下最终返回的节点
head->next->next=head;//交换前面的节点
head->next=tmp;//链接上后面交换好了的节点
return ret;//返回现在的头结点
}
};
其他问题
● while (cur->next != nullptr && cur->next->next != nullptr) 这边为什么是&& 不是|| 一个是对于偶数个结点的判断 一个是奇数个结点 那不应该是||的关系吗?
奇数节点就不需要交换了,所以只有满足后面有偶数个节点的时候才会进入循环
● 循环条件,什么情况应该判断指针本身为空呢?
可以看这个遍历的指针最后需要走到哪里 需不需要对最后一个节点做操作
时间复杂度:O(n)
空间复杂度:O(1)
删除链表的倒数第 N 个结点
19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)
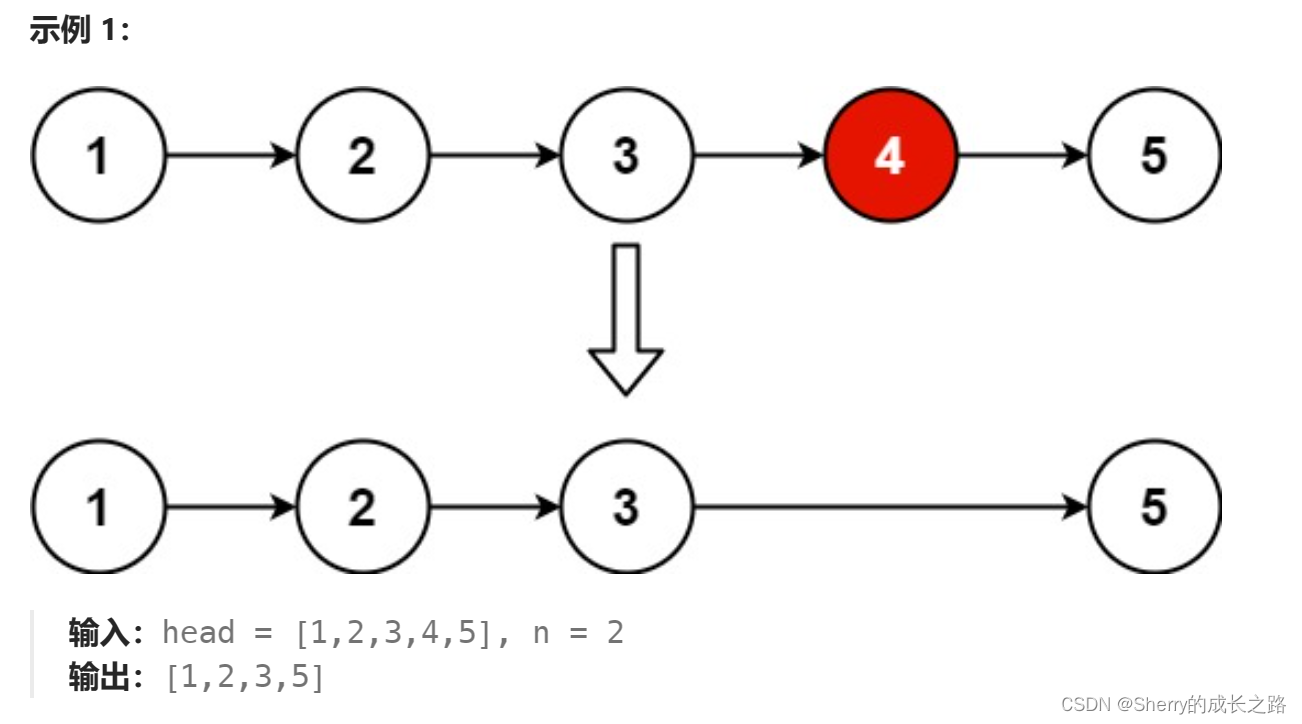
暴力求解
这道题最容易想出的方法是暴力求解,方法是先遍历一遍链表用计数器count数出有多少个链表节点,之后用count减去N,得到的就是正着数第count-N个节点就是我们要删除的节点,然后还是用之前删除链表的思路,先找到要删除节点的前一个节点的next指向要删除节点的next完成删除。
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode*hummyhead=new ListNode(0);
hummyhead->next=head;
ListNode*cur=hummyhead;int count=0;
while(cur->next){
cur=cur->next;count++;
}
int n1=(count-n)>0?count-n:0;cur=hummyhead;
while(n1--){
cur=cur->next;
}
if(count)
cur->next=cur->next->next;
return hummyhead->next;
}
};
此题仍然使用虚拟头节点的方法来写,这样当要删除的节点是头节点的时候,并不需要单独判断情况,节省代码量。
双指针法
而另一种相对省时间一点的方法是双指针法
具体思路为创建快慢指针,一开始均指向虚拟头节点,然后让快指针先走n步,然后快慢再同时往后遍历,直到快指针指向空,此时慢指针所指向的节点则为要删除的节点。
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* slow = dummyHead;
ListNode* fast = dummyHead;
while(n-- && fast != NULL) {
fast = fast->next;
}
fast = fast->next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点
while (fast != NULL) {
fast = fast->next;
slow = slow->next;
}
ListNode *tmp = slow->next;// C++释放内存的逻辑
slow->next = tmp->next;
delete tmp;
return dummyHead->next;
}
};
思路写到这里已经很清晰了,那么为什么我们要将n++之后再走呢?原因也很简单,是为了让快指针fast指向要删除节点的上一个位置,如果不明白这个快慢指针的思路,可以自行在纸上以画图的形式模拟一下。
采用虚拟头结点不需要单独判断头结点是否为空,并且确实很有必要,不然很容易想漏情况,以下是不用虚拟头结点的代码:
class Solution {
public:
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k) {
if(pListHead==nullptr)
{
return nullptr;
}
ListNode* front=pListHead;
ListNode* rear=pListHead;
while (k>0&&front) {
k--;
front=front->next;
}
while (front) {
front=front->next;
rear=rear->next;
}
return k>0?nullptr:rear;
}
};
其他问题
● 链表问题的debug:可以在循环中逻辑执行前打一次输出语句,执行后打一次输出节点值val, 符合预期在增加打输出node.next.val(如果你需要知道后面连接是啥),空针就代表断链了或者其他错误了, 然后这样慢慢增加找, 还有一种就是利用手动画图debug学链表的时候经常画图设计简单case边界case来调试,现在写链表的题都是可以脑子有链表图
时间复杂度: O(n)
空间复杂度: O(1)
环形链表 II
142. 环形链表 II - 力扣(LeetCode)
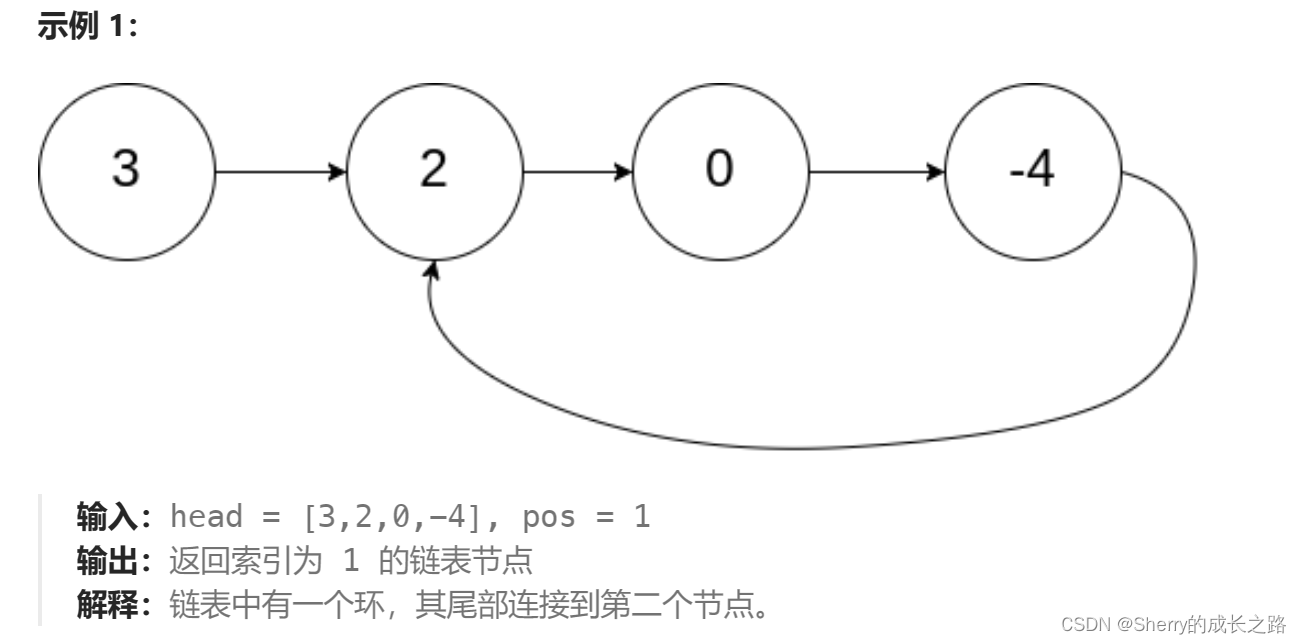
环形链表的基础上,增加了需要判断环的入口的问题,首先是判断链表是否有环,有环的判断是简单的,用双指针方法都从头开始,快指针一次走两个节点,慢指针一次走一个节点,如果相遇则为有环,相遇了之后在相遇点处,用一个指针来指向(slow指针直接向后走也可以)相遇点,然后在头节点再用一个指针指向,两个指针一起走,相遇处则为环的入口。
为什么快慢指针,一定会在有环时相遇呢?如果没有环,那么快指针一定比慢指针走得快所以,不可能相遇,但是如果有环,两指针同时在环内,那就是快指针追逐慢指针,由于快指针一次走两步,慢指针一次走一步,进环后每次运动都相当于两指针距离减少一个节点,相当于慢指针不动,快指针每次走一步,所以有环两节点一定会相遇!但是如果快指针一次走更多步,比如走三步,那么有可能进入环之后,两指针无法相遇,造成死循环。
讲完相遇再说说,第二个关键的步骤,我们假设从起点到换入口距离为x,从入口到相遇点位置距离为y,相遇点再到入口的后半段距离我们设为z,可得慢指针slow走过x+y,而快指针fast走过x+y+n*(y+z),这里的n是fast指针在环内走的圈数,y+z是一圈经过的距离,可得(x+y)2=x+y+n(y+z)化简得x=n*(y+z)-y,单独提出一圈也就是y+z来消去-y得x=(n-1)*(y+z)+z。当n为一圈时,得到x=z的关系。
正是由于这样我们才得到了上述的结论,如果fast指针在圈内转了不止一圈,实际上结果也是一样的因为无论它转了多少圈,最后开始相遇的那一圈,起点是一样的。
如果对以上推理有些疑问,可以参考这篇博客,里面有详细的分析:【链表OJ题(九)】环形链表延伸问题以及相关OJ题
公式推导
这个方法的难点在于公式推导的过程,只要推导出了公式,解题就变得十分简单
结论:一个指针从 相遇点 开始走,一个指针从 链表头 开始走,它们会在 环的入口点 相遇。”
接下来推导公式:
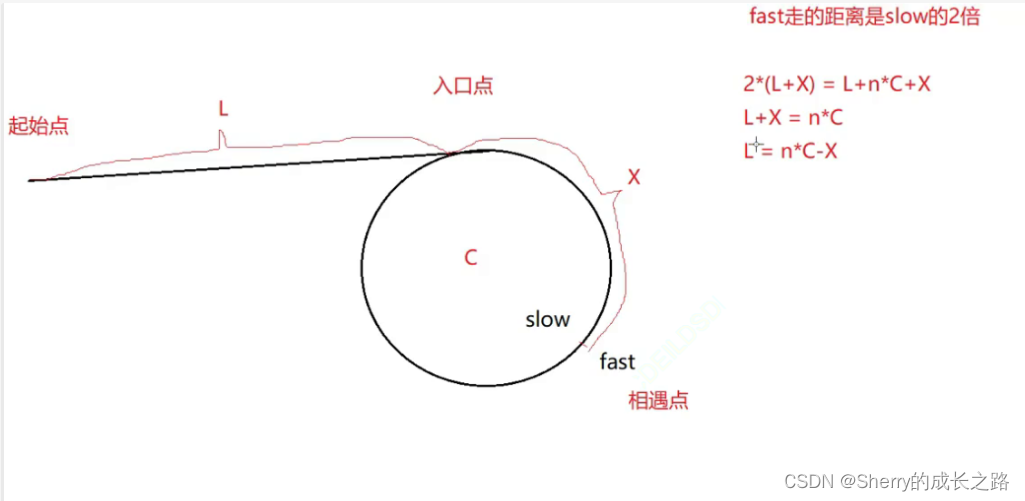
由于 fast 的速度是 slow 的 2 倍。
所以便可以得出这个式子:2 ( L + x ) = L + N * c + x,而这个式子又可以进行推导:
2 ( L + x ) = L + N * c + x
↓
L + x = N * c
↓
L = N * c - x
↓
L = ( N - 1 ) * c + c - x
这里 公式已经推导 完成:L = ( N - 1 ) * c + c - x 。但是这个公式到底是什么意思?
意思是一个指针从起始点开始走,一个指针从相遇点开始走,它们会在环的入口点相遇
根据这个我们也就可以做出这道题目了。
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
// 快慢指针相遇,此时从head 和 相遇点,同时查找直至相遇
if (slow == fast) {
ListNode* index1 = fast;
ListNode* index2 = head;
while (index1 != index2) {
index1 = index1->next;
index2 = index2->next;
}
return index2; // 返回环的入口
}
}
return NULL;
}
};
相交链表
先利用 快慢指针 ,以 环形链表 的解法,找到 fast 和 slow 相交的点。然后将这个 交点 给为 meetnode 。作为两条新链表的尾。那么 meetnode->next 为某条新链表的头。然后 入环点 ,就可以看做是两条链表的交点。然后就是 相交链表 的做法
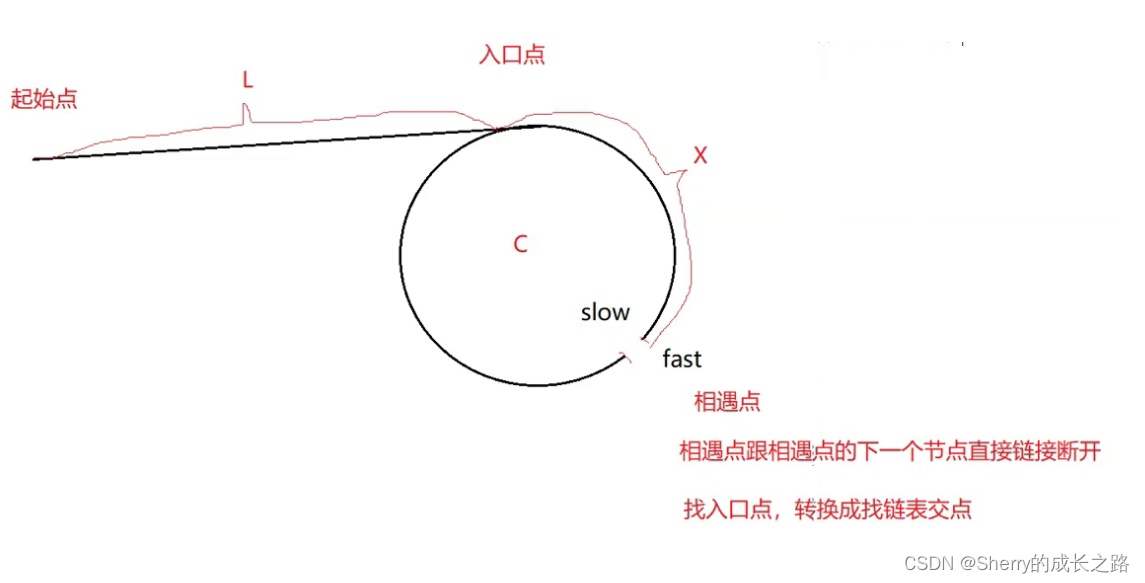
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* curA = headA;
ListNode* curB = headB;
int lenA = 0, lenB = 0;
while (curA != NULL) { // 求链表A的长度
lenA++;
curA = curA->next;
}
while (curB != NULL) { // 求链表B的长度
lenB++;
curB = curB->next;
}
curA = headA;
curB = headB;
// 让curA为最长链表的头,lenA为其长度
if (lenB > lenA) {
swap (lenA, lenB);
swap (curA, curB);
}
// 求长度差
int gap = lenA - lenB;
// 让curA和curB在同一起点上(末尾位置对齐)
while (gap--) {
curA = curA->next;
}
// 遍历curA 和 curB,遇到相同则直接返回
while (curA != NULL) {
if (curA == curB) {
return curA;
}
curA = curA->next;
curB = curB->next;
}
return NULL;
}
};
时间复杂度:O(n + m)
空间复杂度:O(1)
总结:
今天的三道题也算是复习回顾了,但对递归有了新的理解。接下来,我们继续进行算法练习·。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~