举个例子，“明天如果下雨我就不出门了。” 在这里我们用了一个决策条件:是否下雨，然后基于这个条件会有不同的结果:出门和不出门。 这就是一个经典的决策树!

决策树的核心组成部分---节点  边 

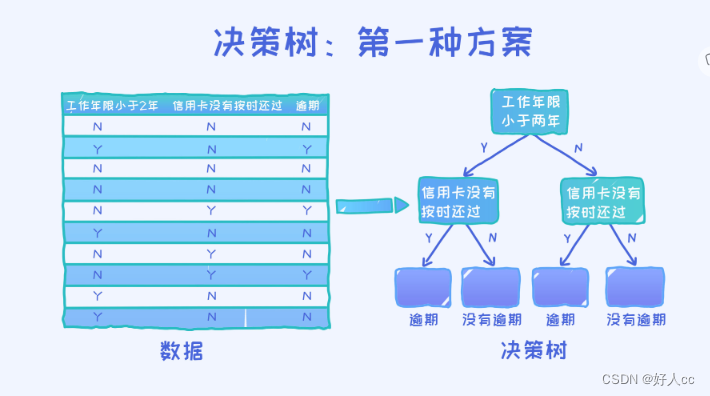
最后的结论就是第一个决策树要优于第二个决策树，因为它的准确率更高。由于这个问题本身及其简单，所以我们甚至都可以罗列出所有可能的决策树，然后再判断哪一个最好。但实际上，稍微复杂点的问题就不太可能这么做了，因为所有可能的决策树数量太多，不可能一一罗列。

不确定性的减少

 已经知道如何用数学来表示不确定性了。 接下来，我们再回到决策树的问题上。那又如何表示不确定性的减少呢? 无非就是原来的不确定性减去现在的不确定性!下面我们试图分别对”是否发烧“和“是否疼痛”两个特征，分别计算一下不确定性的减少。

构造决策树的时候，每一步都要根据不确定性（信息熵），来选择这棵树的当前的根节点。

这种不确定性的减少也叫作信息增益(information gain)。构建决策树的过程无非是每一步通过信息增益来选择最好的特征作为当前的根节点，以此类推，持续把树构造起来。下面，我们通过一个稍微复杂一点的例子来说明一棵决策树的构建的完整过程。

构建决策树的整体过程

每个都做不确定性减小的计算，哪个最大，就把哪个当作根节点

以上是决策树的构建过程。总结一下，每一步的构建其实就是选择当前最好的特征作为根节点。然后持续地重复以上过程把整棵树构建起来。其中，信息增益充当着每次选择特征的标准。当然，除了信息增益，我们也可以选择其他的指标作为选择特征的标准。到此为止，决策树的构建过程已经说完了。除了这些其实还有几个重要问题需要考虑，比如如何让决策树避免过拟合、如何处理连续型特征、如何使用决策树来解决回归问题等。

对决策树调参的时候，无非主要来调整树的深度、每一个叶节点样本的个数等等。具体最优的参数一般通过交叉验证的方式来获得，这一点跟其他模型是一样的。

处理连续型变量

我们来学习一下如何处理连续型特征以及用决策树来解决回归问题。如果一个特征是离散型特征，处理方式是比较直观的，无非就是针对每一个特征创建一个分支。但对于连续型特征倒是没有那么直观，感觉有点没有头绪。连续型特征的处理上其实有很多种方法。对于连续型特征，我们可能会有“如果一个年龄大于20”，则怎么怎么样，不到20再怎么怎么样。所以这里的核心问题是数字“20”，也叫作阈值。

决策树回归

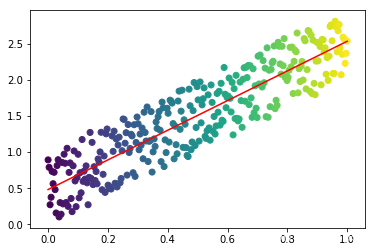
回归问题是指在统计学和机器学习中，根据已知数据的特征，建立一个数学模型来预测一个连续型的因变量。换句话说，回归问题是用于预测或估计数值型输出的问题。

当我们使用决策树解决分类问题时，可以计算准确率来评估一个决策树的好坏。但对于回归问题则需要使用不同的指标，其中一个常用的指标叫作MSE(mean square error)，也是线性回归模型所使用的评估标准。

针对于回归问题的总结。唯一的区别是把分类问题里的信息熵替换成了变量的标准差。