这里写目录标题
- AlexNet
- 参考文章
- AlexNet模型结构
- AlexNet共8层:
- AlexNet运作流程
- 简单代码实现
- 重要说明
- 重要技巧
- 主要贡献
AlexNet
AlexNet 是一种卷积神经网络(Convolutional Neural Network,CNN)的架构。它是由Alex Krizhevsky、Ilya Sutskever和Geoffrey Hinton提出的,并在2012年的ImageNet大规模视觉识别挑战赛(ILSVRC)中获胜。
AlexNet是推动深度学习在计算机视觉任务中应用的先驱之一
AlexNet跟LeNet-5类似也是一个用于图像识别的卷积神经网络。AlexNet网络结构更加复杂,参数更多。
验证了深度卷积神经网络的高效性
参考文章
手撕 CNN 经典网络之 AlexNet(理论篇)
论文《ImageNet Classification with Deep Convolutional Neural Networks》
【动手学计算机视觉】第十六讲:卷积神经网络之AlexNet
AlexNet模型结构
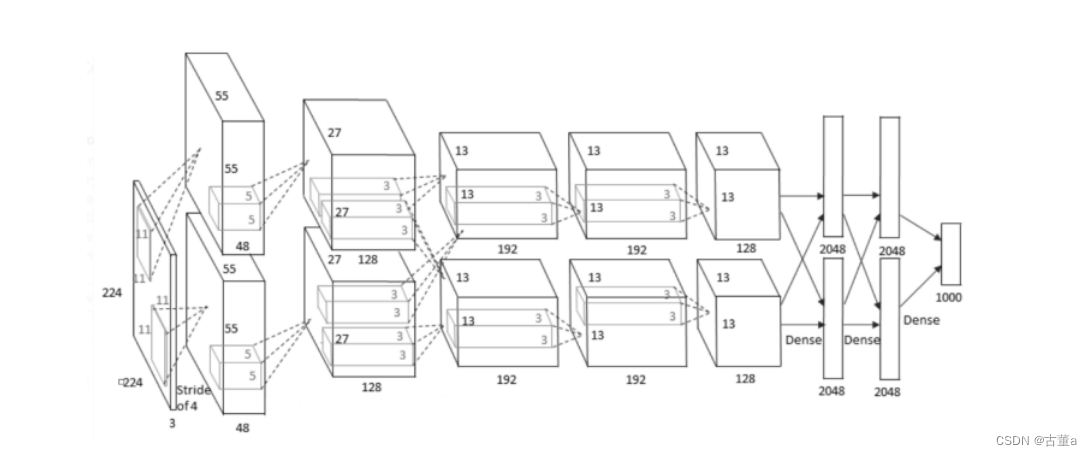
AlexNet中使用的是ReLU激活函数,它5层卷积层除了第一层卷积核为
11
∗
11
11*11
11∗11、第二次为
5
∗
5
5*5
5∗5之外,其余三层均为
3
∗
3
3*3
3∗3
1. 第一层:卷积层
输入
输入为 224 ∗ 224 ∗ 3 224 * 224 * 3 224∗224∗3的图像,输入之前进行了去均值处理(AlexNet对数据集中所有图像向量求均值,均值为 224 ∗ 224 ∗ 3 224 * 224 * 3 224∗224∗3,去均值操作为原图减去均值,绝对数值对分类没有意义,去均值之后的相对数值可以正确分类且计算量小)
卷积
卷积核的数量为96,论文中两块GPU分别计算48个核;
卷积核大小 11 ∗ 11 ∗ 3 , s t r i d e = 4 11 * 11 * 3,stride=4 11∗11∗3,stride=4,stride表示的是步长,padding = 0,表示不填充边缘。
卷积后的图形大小:
w
i
d
e
=
(
224
−
k
e
r
n
e
l
_
s
i
z
e
+
2
∗
p
a
d
d
i
n
g
)
/
s
t
r
i
d
e
+
1
=
54
wide = (224 - kernel\_size+2 * padding) / stride + 1 = 54
wide=(224−kernel_size+2∗padding)/stride+1=54
h
e
i
g
h
t
=
(
224
−
k
e
r
n
e
l
_
s
i
z
e
+
2
∗
p
a
d
d
i
n
g
)
/
s
t
r
i
d
e
+
1
=
54
height = (224 - kernel\_size+2 * padding) / stride + 1 = 54
height=(224−kernel_size+2∗padding)/stride+1=54
d
i
m
e
n
t
i
o
n
=
96
dimention = 96
dimention=96
参考个数: ( 11 × 11 × 3 + 1 ) × 96 = 35 k (11 \times 11 \times 3 + 1) \times 96 = 35k (11×11×3+1)×96=35k

池化
输入通道数根据输入图像而定,输出通道数为96,步长为4。

注:窗口大小3*3,步长2,池化过程出现重叠,现在一般不使用重叠池化。
池化结果:27x27x96 特征图组
局部响应归一化层(Local Response Normalized)

为什么要引入LRN层?
首先要引入一个神经生物学的概念:侧抑制(lateral inhibitio),即指被激活的神经元抑制相邻的神经元。
归一化(normaliazation)的目的就是“抑制”,LRN就是借鉴这种侧抑制来实现局部抑制,尤其是我们使用RELU的时候,这种“侧抑制”很有效 ,因而在AlexNet里使用有较好的效果。
归一化有什么好处?
1 归一化有助于快速收敛;
2 对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。
【补充:神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
深度网络的训练是复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。】
2. 第二层:卷积层
输入为上一层卷积的 feature map,
27
×
27
×
96
27 \times 27 \times 96
27×27×96大小的特诊图组。
卷积核的个数为256个,论文中的两个GPU分别有128个卷积核。
卷积核大小
5
∗
5
5*5
5∗5,输入通道数为96,输出通道数为256,步长为2,padding = 2。
卷积结果:
(
27
−
5
+
2
×
2
)
/
1
+
1
,
27
×
27
×
256
(27 - 5 + 2 \times 2) / 1 + 1,27 \times 27 \times 256
(27−5+2×2)/1+1,27×27×256的特征图组。
然后做LRN。
最后最大化池化
池化层窗口大小为3*3,步长为2。
池化结果:
13
×
13
×
256
13 \times 13 \times 256
13×13×256的特征图组。

3. 第三层:卷积层
输入为第二层的输出,没有LRN和Pool。
卷积核大小
3
∗
3
3*3
3∗3,输入通道数为256,输出通道数为384,stride为1,padding = 1。
图像尺寸为:
(
13
−
3
+
2
×
1
)
/
1
+
1
=
13
(13 - 3 + 2 \times 1) / 1 + 1 = 13
(13−3+2×1)/1+1=13
输出:
13
×
13
×
384
13 \times 13 \times 384
13×13×384
4. 第四层:卷积层
输入为第三层的输出,没有LRN和Pool。
卷积核个数为384,大小
3
∗
3
3*3
3∗3,输入通道数为384,输出通道数为384,stride为1,padding = 1。
图像尺寸为:
(
13
−
3
+
2
×
1
)
/
1
+
1
=
13
(13 - 3 + 2 \times 1) / 1 + 1 = 13
(13−3+2×1)/1+1=13
输出:
13
×
13
×
384
13 \times 13 \times 384
13×13×384
5. 第五层:卷积层
输入为第四层的输出。
卷积核大小
3
∗
3
3*3
3∗3,输入通道数为384,输出通道数为256,stride为1,padding = 1。
图像尺寸为:
(
13
−
3
+
2
×
1
)
/
1
+
1
=
13
(13 - 3 + 2 \times 1) / 1 + 1 = 13
(13−3+2×1)/1+1=13
卷积结果为:
13
×
13
×
256
13 \times 13 \times 256
13×13×256
池化层窗口大小为
3
∗
3
3*3
3∗3,步长为2。
图像尺寸为:
(
13
−
3
)
/
2
+
1
=
6
(13 - 3) / 2 + 1 = 6
(13−3)/2+1=6
池化结果为:
6
×
6
×
256
6 \times 6 \times 256
6×6×256
6. 第六层:全连接层
输入大小为上一层的输出,输出大小为4096。
Dropout概率为0.5。
7. 第七层:全连接层
输入大小为上一层的输出,输出大小为4096。
Dropout概率为0.5。
8. 第八层:全连接层
输入大小为4096,输出大小为分类数。
Dropout概率为0.5。

需要将第五层池化结果6×6×256转换为向量9216×1。因为全连接层不能输入矩阵,要输入向量。
注意: 需要注意一点,5个卷积层中前2个卷积层后面都会紧跟一个池化层,而第3、4层卷积层后面没有池化层,而是连续3、4、5层三个卷积层后才加入一个池化层。
AlexNet共8层:
- 5个卷积层(CONV1——CONV5)
- 3个全连接层(FC6-FC8)

AlexNet运作流程
- conv1:输入→卷积→ReLU→局部响应归一化→重叠最大池化层
- conv2:卷积→ReLU→局部响应归一化→重叠最大池化层
- conv3:卷积→ReLU
- conv4:卷积→ReLU
- conv5:卷积→ReLU→重叠最大池化层(经过这层之后还要进行flatten展平操作)
- FC1:全连接→ReLU→Dropout
- FC2:全连接→ReLU→Dropout
- FC3(可看作softmax层):全连接→ReLU→Softmax
简单代码实现
使用pytorch
import torch
import torch.nn as nn
class AlexNet(nn.Module):
def __init__(self, num_classes=1000):
super(AlexNet, self).__init__()
# 第一个卷积层,输入通道3(RGB图像),输出通道64,卷积核大小11x11,步长4,填充2
self.conv1 = nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2)
self.relu1 = nn.ReLU(inplace=True)
# 最大池化层,窗口大小3x3,步长2
self.maxpool1 = nn.MaxPool2d(kernel_size=3, stride=2)
# 第二个卷积层,输入通道64,输出通道192,卷积核大小5x5,填充2
self.conv2 = nn.Conv2d(64, 192, kernel_size=5, padding=2)
self.relu2 = nn.ReLU(inplace=True)
# 第二个最大池化层,窗口大小3x3,步长2
self.maxpool2 = nn.MaxPool2d(kernel_size=3, stride=2)
# 第三个卷积层,输入通道192,输出通道384,卷积核大小3x3,填充1
self.conv3 = nn.Conv2d(192, 384, kernel_size=3, padding=1)
self.relu3 = nn.ReLU(inplace=True)
# 第四个卷积层,输入通道384,输出通道256,卷积核大小3x3,填充1
self.conv4 = nn.Conv2d(384, 256, kernel_size=3, padding=1)
self.relu4 = nn.ReLU(inplace=True)
# 第五个卷积层,输入通道256,输出通道256,卷积核大小3x3,填充1
self.conv5 = nn.Conv2d(256, 256, kernel_size=3, padding=1)
self.relu5 = nn.ReLU(inplace=True)
# 第三个最大池化层,窗口大小3x3,步长2
self.maxpool3 = nn.MaxPool2d(kernel_size=3, stride=2)
# 自适应平均池化层,输出特征图大小为6x6
self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
# 全连接层,输入大小为256x6x6,输出大小为4096
self.fc1 = nn.Linear(256 * 6 * 6, 4096)
self.relu6 = nn.ReLU(inplace=True)
# 全连接层,输入大小为4096,输出大小为4096
self.fc2 = nn.Linear(4096, 4096)
self.relu7 = nn.ReLU(inplace=True)
# 全连接层,输入大小为4096,输出大小为num_classes
self.fc3 = nn.Linear(4096, num_classes)
def forward(self, x):
x = self.conv1(x)
x = self.relu1(x)
x = self.maxpool1(x)
x = self.conv2(x)
x = self.relu2(x)
x = self.maxpool2(x)
x = self.conv3(x)
x = self.relu3(x)
x = self.conv4(x)
x = self.relu4(x)
x = self.conv5(x)
x = self.relu5(x)
x = self.maxpool3(x)
x = self.avgpool(x)
x = x.view(x.size(0), -1)
x = self.fc1(x)
x = self.relu6(x)
x = self.fc2(x)
x = self.relu7(x)
x = self.fc3(x)
return x
# 创建AlexNet模型的实例
model = AlexNet(num_classes=1000)
# 打印模型结构
print(model)
重要说明
- 用于提取图像特征的卷积层以及用于分类的全连接层是同时学习的。
- 卷积层与全连接层在学习过程中会相互影响、相互促进
重要技巧
- Dropout策略防止过拟合;
- 使用动量的随机梯度下降算法,加速收敛;
- 验证集损失不下降时,手动降低10倍的学习率;
- 采用样本增强策略增加训练样本数量,防止过拟合;
- 集成多个模型,进一步提高精度。
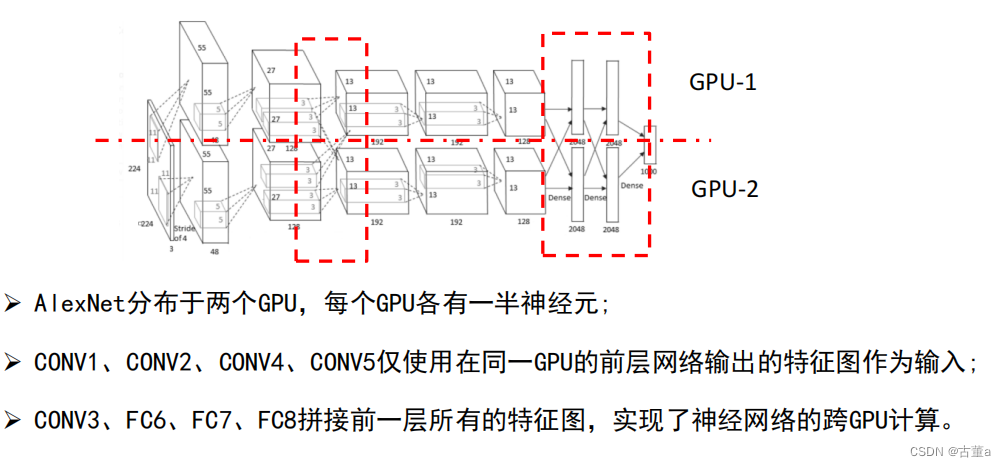
现在显存基本都够用,不需要再考虑分两个GPU计算。
AlexNet卷积层在做什么?

主要贡献
- 提出了一种卷积层加全连接层的卷积神经网络结构
- 首次使用ReLU函数做为神经网络的激活函数
- 首次提出Dropout正则化来控制过拟合
- 使用加入动量的小批量梯度下降算法加速了训练过程的收敛
- 使用数据增强策略极大地抑制了训练过程的过拟合
- 利用了GPU的并行计算能力,加速了网络的训练与推断