🍒题目

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

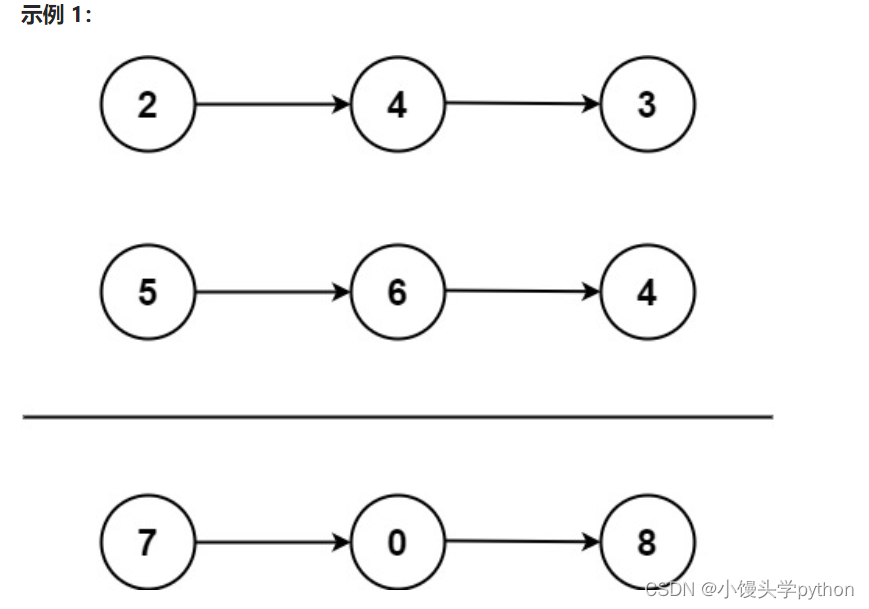
本道题，我们采用两个主流的思路，迭代、递归，下面我们首先从迭代开始说起

---

🍒解法一 迭代

在开始编写代码之前，我们有必要了解这道题的思路，当我们读完题会感觉这题好像也就那么回事，正常加法嘛，但是上手就不知所措了

这题的核心思路主要是那个进一，还有就是l1和l2长度的问题

这题的解决配合了余数和商，在Python中就是==//(整除)、%==（取余）
好吧那么我们就可以想一下，我们可以将l1和l2的节点值相加，得到值如果整除后大于0，则作为进位值；得到的值取余即为要保存的节点
接下来我们看看代码

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        q = p = ListNode(None)          
        s = 0               # 令初始进位值为0
        while l1 or l2 or s:
            s += (l1.val if l1 else 0) + (l2.val if l2 else 0)  
            p.next = ListNode(s % 10)      
            p = p.next                     
            s //= 10                        
            l1 = l1.next if l1 else None    
            l2 = l2.next if l2 else None    
        return q .next   

---

🍒解法二 递归

递归对我，对于好多人应该都属于比较难的解法，想到了不会用，要不就是想不到哈哈哈

class Solution:
    # l1 和 l2 为当前遍历的节点，carry 为进位
    def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode], carry=0) -> Optional[ListNode]:
        if l1 is None and l2 is None:  # 递归边界：l1 和 l2 都是空节点
            return ListNode(carry) if carry else None  # 如果进位了，就额外创建一个节点
        if l1 is None:  # 如果 l1 是空的，那么此时 l2 一定不是空节点
            l1, l2 = l2, l1  # 交换 l1 与 l2，保证 l1 非空，从而简化代码
        carry += l1.val + (l2.val if l2 else 0)  # 节点值和进位加在一起
        l1.val = carry % 10  # 每个节点保存一个数位
        l1.next = self.addTwoNumbers(l1.next, l2.next if l2 else None, carry // 10)  # 进位
        return l1

复杂度分析

上面的代码片是我从力扣看到的，出自某位大佬手笔，喜欢这个方法的可以看看！

---

🍒递归小案例

当谈到递归时，经典的案例是计算阶乘、斐波那契数列和二叉树遍历。下面是这些案例的简单示例：

下面我展示一下数据结构中的二叉树遍历和斐波那契数列

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def preorder_traversal(node):
    if node:
        print(node.value)
        preorder_traversal(node.left)
        preorder_traversal(node.right)

def inorder_traversal(node):
    if node:
        inorder_traversal(node.left)
        print(node.value)
        inorder_traversal(node.right)

def postorder_traversal(node):
    if node:
        postorder_traversal(node.left)
        postorder_traversal(node.right)
        print(node.value)

# 创建一个示例二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print("前序遍历:")
preorder_traversal(root)

print("中序遍历:")
inorder_traversal(root)

print("后序遍历:")
postorder_traversal(root)

运行结果如下

下面的斐波那契数列

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

result = fibonacci(6)
print(result) 

运行结果如下

🍒迭代 VS 递归

迭代和递归是两种不同的问题解决方法，它们在编程中经常被用来解决各种问题，但它们有不同的工作方式和应用场景。

迭代（Iteration）：

    工作原理：迭代是通过循环来重复执行一段代码，每次迭代都使用前一次迭代的结果来计算下一次的结果。这种方式通常使用for循环或while循环来实现。

    优点：
        迭代通常比递归更容易理解和调试，因为它们遵循直线性的执行流程。
        迭代通常更节省内存，因为不需要在每个递归调用之间存储调用堆栈。

    适用场景：当问题可以被划分为一系列重复的步骤，并且每个步骤都可以直接计算时，迭代通常是更好的选择。例如，遍历数组、计算阶乘等。

递归（Recursion）：

    工作原理：递归是一个函数调用自身的过程，每个递归调用都会将问题分解为更小的子问题，直到达到基本情况（递归终止条件），然后开始合并这些子问题的结果来解决原始问题。

    优点：
        递归可以更自然地表达某些问题，特别是涉及到树状结构（例如二叉树、图）的问题。
        递归可以减少代码的复杂性，因为它允许将问题划分为更小的部分。

    适用场景：递归通常在问题的解决方案与其子问题的解决方案具有相似结构时非常有用。例如，树的遍历、斐波那契数列等。

比较迭代和递归的选择取决于问题的性质和个人偏好。在一些情况下，迭代更高效且更容易实现，而在另一些情况下，递归更自然且更易于理解。有时候，甚至可以将两者结合使用，例如在迭代过程中调用递归函数来处理特定的子问题。

最终，选择使用哪种方法取决于问题的具体要求以及编程语言和环境的支持。

---

挑战与创造都是很痛苦的，但是很充实。