无线定位中TDOA时延估计算法matlab仿真

news2025/1/11 23:58:45

1.算法运行效果图预览

2.算法运行软件版本

3.部分核心程序

4.算法理论概述

5.算法完整程序工程

1.算法运行效果图预览

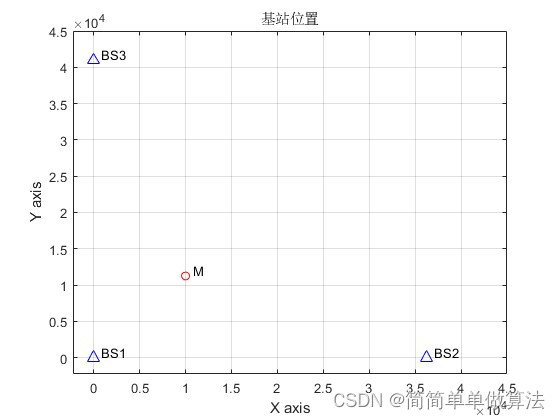
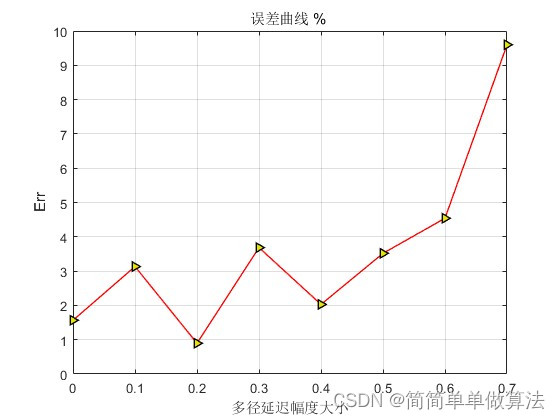
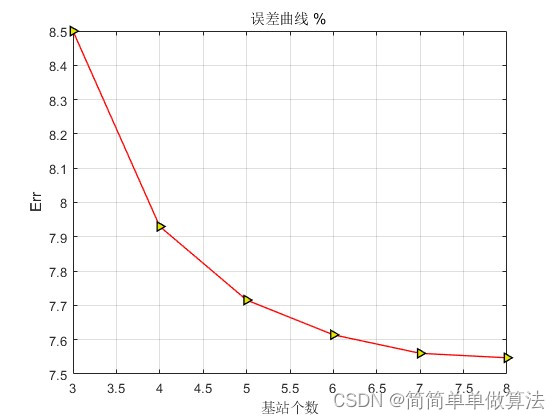
2.算法运行软件版本

matlab2022a

3.部分核心程序

...................................................................

figure;
plot(P1x,P1y,'b^','Markersize',8);
hold on;
plot(P2x,P2y,'b^','Markersize',8);
hold on;
plot(P3x,P3y,'b^','Markersize',8);
hold on;
text(P1x+800,P1y+800,'BS1');
text(P2x+800,P2y+800,'BS2');
text(P3x+800,P3y+800,'BS3');
xlabel('X axis');
ylabel('Y axis');
axis([-3*LL/20,3*LL,-3*LL/20,3*LL]);
grid on;
%这里随机生成移动物体的位置坐标
P0x = 2*LL/3;
P0y = 3*LL/4;
plot(P0x,P0y,'ro','Markersize',6);hold off;
text(P0x+800,P0y+800,'M');
title('基站位置');


%定义发送信号，这里发送信号根据要求使用AM发送信号
fc     = 1000;   %载波频率
tau    = 10^(-7);%时间间隔
T      = 1/fc/2; %频率周期
t      = -T*SL+tau:tau:T*SL;%信号的长度，这里使用8个周期进行
No     = length(t);       %信号的长度
A      = 1;%发送信号的幅度
s      = A*cos(2*pi*fc*t);
rng(1);%use matlab2013b else maybe error
%信道模拟
for j = 1:length(SNR)
    %加入噪声
    r2(1,:) = awgn(r(1,:),SNR(j));
    r2(2,:) = awgn(r(2,:),SNR(j));
    r2(3,:) = awgn(r(3,:),SNR(j));
    
    %加入多径 
    for jj = 1:N
        signals  = r2(jj,:);
        if Mpd == 0
           signals2 = signals;
        else
           signals2 = signals + 0.65*[zeros(1,Mpd),signals(1:end-Mpd)];   
        end
        r3(jj,:) = signals2;
    end
    %计算延迟相关运算
    Peak         = zeros(N,1);%定义相关峰的值
    delay_theory = zeros(N,1);%通过广义相关运算得到的延迟估计值
    for kk = 1:1:LL/10
        tau_theory = tau*kk;
        temp       = r3(1,(No/2-kk+1):(No-kk))*tau;
        for i =2:N
            data   = (sum(r3(i,No/2+1:No).*temp))^2;
            if Peak(i) < data
                Peak(i) = data;
                delay_theory(i) = tau_theory;
            end
        end
    end

    %通过TDOA方法，根据理论估计延迟得到实际的坐标点位置
    R_theory = zeros(1,N);
    Kj       = zeros(1,N);
    for i = 2:N
        R_theory(i) = delay_theory(i)*c;
        Kj(i)       = BS(i,1)^2 + BS(i,2)^2;
    end
.................................................................
     
    clear xyChan R1 cs bs as Q_tdoa K_tdoa D_tdoa C_tdoa H_tdoa Kj R_theory delay_theory Peak tau_theory temp
end

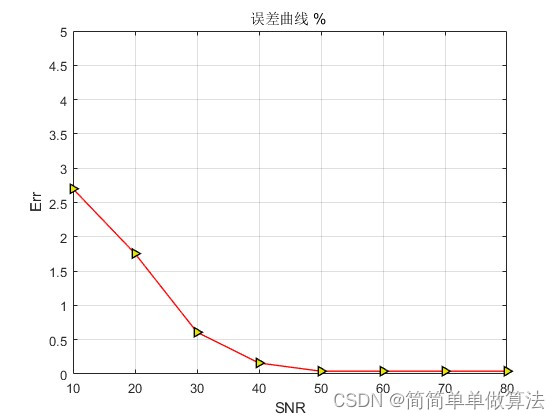
figure;
plot(SNR,Err,'-r>',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
grid on;
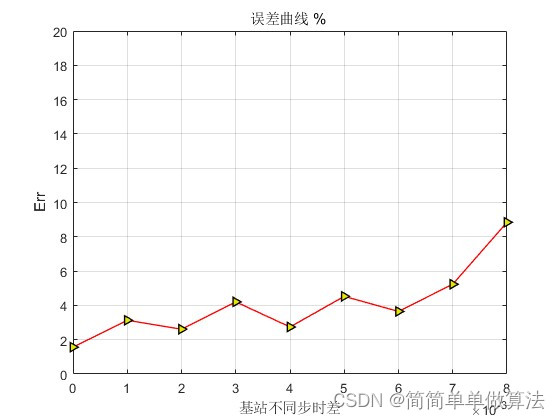
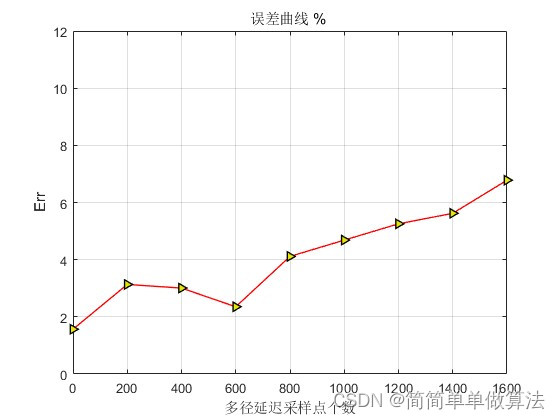
title('误差曲线 % ');
xlabel('SNR');
ylabel('Err');
axis([10,80,0,5]);
 
%显示理论估计值
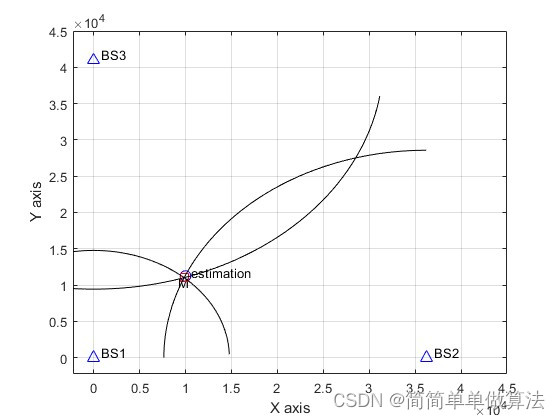
figure;
plot(P1x,P1y,'b^','Markersize',8);hold on;
plot(P2x,P2y,'b^','Markersize',8);hold on;
plot(P3x,P3y,'b^','Markersize',8);hold on;
axis([-3*LL/20,3*LL,-3*LL/20,3*LL]);
grid on;
xlabel('X axis');
ylabel('Y axis');
text(P1x+800,P1y+800,'BS1');
text(P2x+800,P2y+800,'BS2');
text(P3x+800,P3y+800,'BS3');
plot(P0x,P0y,'bo','Markersize',8);
hold on;
text(P0x-800,P0y-800,'M');

SEL = 1;

plot(X_theory(SEL),Y_theory(SEL),'rs','Markersize',8);hold on;
text(X_theory(SEL)+800,Y_theory(SEL)+800,'estimation');

R1 = sqrt((X_theory(SEL)-P1x)^2+(Y_theory(SEL)-P1y)^2); 
R2 = sqrt((X_theory(SEL)-P2x)^2+(Y_theory(SEL)-P2y)^2); 
R3 = sqrt((X_theory(SEL)-P3x)^2+(Y_theory(SEL)-P3y)^2);

alpha=0.01*pi:pi/100:0.55*pi;                     
x1= P1x+R1*cos(alpha); 
y1= P1y+R1*sin(alpha); 
hold on;
plot(x1,y1,'k-'); 

alpha=0.5*pi:pi/100:1.0*pi;                    
x2= P2x+R2*cos(alpha); 
y2= P2y+R2*sin(alpha); 
hold on;
plot(x2,y2,'k-'); 

alpha=1.1*pi:pi/100:1.95*pi;                    
x3= P3x+R3*cos(alpha); 
y3= P3y+R3*sin(alpha); 
hold on;
plot(x3,y3,'k-'); 
36_005m