怒刷LeetCode的第10天（Java版）

第一题

题目来源

题目内容

解决方法

方法一：两次拓扑排序

第二题

题目来源

题目内容

解决方法

方法一：分治法

方法二：优先队列（Priority Queue）

方法三：迭代

第三题

题目来源

题目内容

解决方法

方法一：迭代

方法二：递归

方法三：双指针

方法四：栈

第一题

题目来源

2603. 收集树中金币 - 力扣（LeetCode）

题目内容

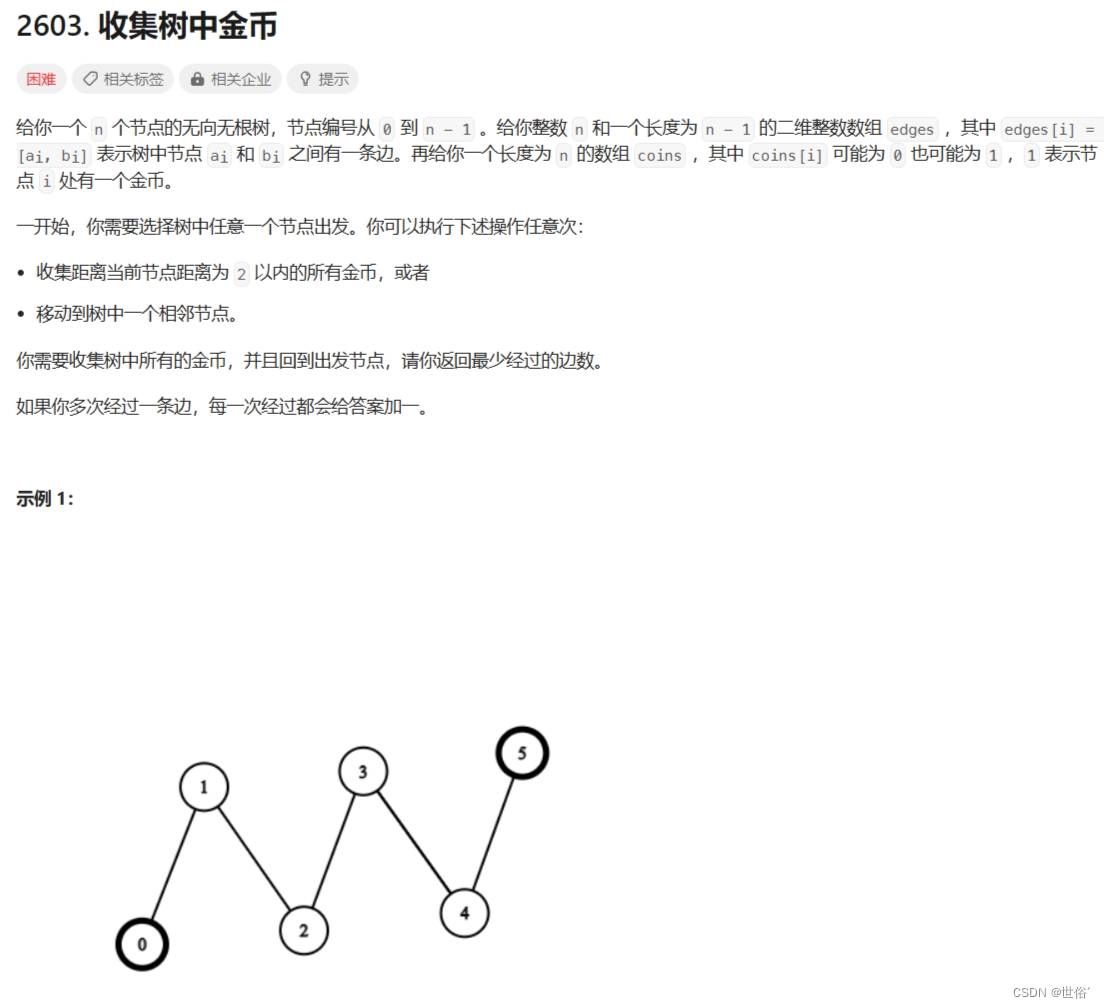
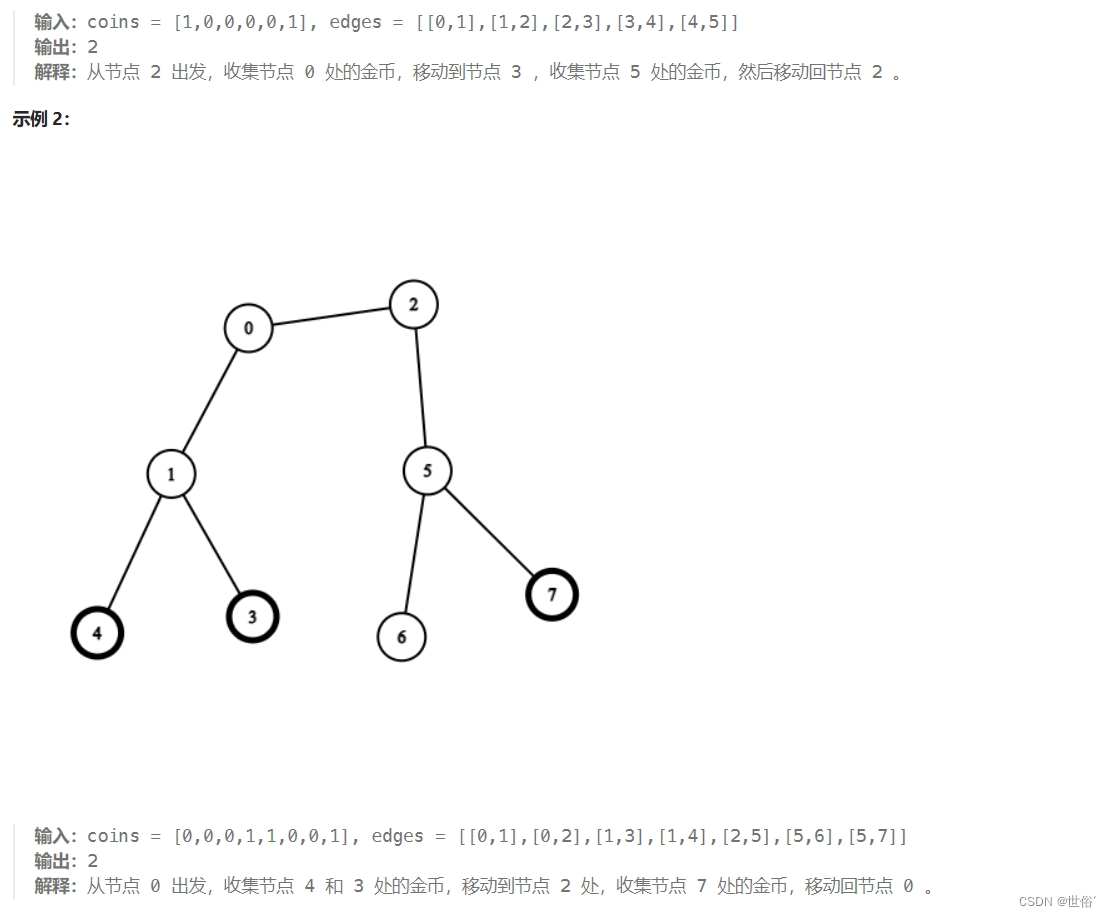
解决方法

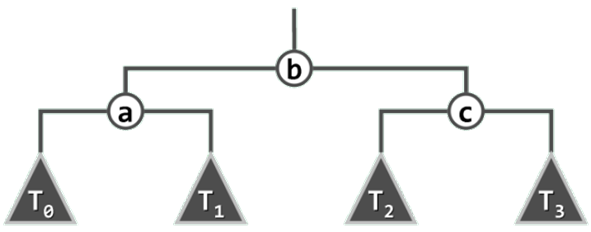
方法一：两次拓扑排序

这个解法的思路如下：

首先，初始化一个邻接表 g，用于存储树的结构，以及一个数组 degree，用于记录每个节点的度数。
遍历边的数组 edges，将每条边的两个节点之间建立连接关系，并更新节点的度数。
初始化一个队列 queue，用于存储无金币的叶子节点。
遍历所有节点，如果一个节点的度数为1并且该节点没有金币，则将其加入队列。
开始循环，直到队列为空。在每次迭代中，取出队列的首个节点 u。
将节点 u 的度数减1，剩余节点数 rest 减1。
遍历与节点 u 相邻的所有节点 v，将其度数减1。
如果节点 v 的度数为1并且该节点没有金币，则将其加入队列。
重复步骤 5-8，直到队列为空。
重复两次以下步骤（总共遍历两次）： a. 初始化一个新的队列 queue。 b. 遍历所有节点，将度数为1的节点加入队列。 c. 开始循环，直到队列为空。 d. 取出队列的首个节点 u，将其度数减1，剩余节点数 rest 减1。 e. 遍历与节点 u 相邻的所有节点 v，将其度数减1。 f. 重复步骤 d-e，直到队列为空。
返回结果，如果剩余节点数 rest 为0，则路径长度为0；否则，路径长度为 (rest - 1) * 2。

这样，通过删除树中无金币的叶子节点和维护节点的度数，可以得到最小路径长度。

class Solution {
    public int collectTheCoins(int[] coins, int[][] edges) {
        int n = coins.length;
        List<Integer>[] g = new List[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new ArrayList<Integer>();
        }
        int[] degree = new int[n];
        for (int[] edge : edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
            ++degree[x];
            ++degree[y];
        }

        int rest = n;
        /* 删除树中所有无金币的叶子节点，直到树中所有的叶子节点都是含有金币的 */
        Queue<Integer> queue = new ArrayDeque<Integer>();
        for (int i = 0; i < n; ++i) {
            if (degree[i] == 1 && coins[i] == 0) {
                queue.offer(i);
            }
        }
        while (!queue.isEmpty()) {
            int u = queue.poll();
            --degree[u];
            --rest;
            for (int v : g[u]) {
                --degree[v];
                if (degree[v] == 1 && coins[v] == 0) {
                    queue.offer(v);
                }
            }
        }
        /* 删除树中所有的叶子节点, 连续删除2次 */
        for (int x = 0; x < 2; ++x) {
            queue = new ArrayDeque<Integer>();
            for (int i = 0; i < n; ++i) {
                if (degree[i] == 1) {
                    queue.offer(i);
                }
            }
            while (!queue.isEmpty()) {
                int u = queue.poll();
                --degree[u];
                --rest;
                for (int v : g[u]) {
                    --degree[v];
                }
            }
        }

        return rest == 0 ? 0 : (rest - 1) * 2;
    }
}

复杂度分析：

1、构建邻接表和计算节点度数的复杂度：

遍历边的数组 edges，时间复杂度为 O(m)，其中 m 是边的数量。
初始化邻接表 g 的空间复杂度为 O(n)，其中 n 是节点的数量。
更新节点度数的过程需要遍历所有边，时间复杂度为 O(m)。

2、删除无金币叶子节点的过程的复杂度：

初始化队列的时间复杂度为 O(n)，其中 n 是节点的数量。
每个节点最多被处理一次，因此删除过程的时间复杂度为 O(n)。

3、连续删除两次叶子节点的过程的复杂度：

需要进行两次完整的节点遍历，因此时间复杂度为 O(2n) = O(n)，其中 n 是节点的数量。

综上所述，整个解法的时间复杂度为 O(m + n)，其中 m 是边的数量，n 是节点的数量。空间复杂度为 O(n)，用于存储邻接表和节点度数。

LeetCode运行结果：

第二题

题目来源

23. 合并 K 个升序链表 - 力扣（LeetCode）

题目内容

解决方法

方法一：分治法

这是一个合并K个升序链表的问题，可以使用分治法来解决。使用了分治法来将k个链表分成两部分进行合并，然后再将合并后的结果继续与剩下的链表合并，直到最终合并成一个升序链表。在每个合并的过程中，可以使用双指针来逐个比较两个链表的节点值，将较小的节点连接到结果链表上。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
public class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }

        return merge(lists, 0, lists.length - 1);
    }

    private ListNode merge(ListNode[] lists, int start, int end) {
        if (start == end) {
            return lists[start];
        }

        int mid = start + (end - start) / 2;
        ListNode left = merge(lists, start, mid);
        ListNode right = merge(lists, mid + 1, end);

        return mergeTwoLists(left, right);
    }

    private ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        }
        if (l2 == null) {
            return l1;
        }

        if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

复杂度分析：

这个解法的时间复杂度是 O(Nlogk)，其中 N 是所有链表的节点总数，k 是链表的数量。因为在每层合并的过程中，需要遍历 N 个节点来比较值，并且每次合并的链表数量减半，因此总共需要合并 logk 层。所以时间复杂度是 O(Nlogk)。
空间复杂度是 O(logk)，主要是递归调用栈的空间。在每一层递归中，都会创建两个新的递归函数调用，所以递归的层数最多是 logk。因此，空间复杂度是 O(logk)。

需要注意的是，这里的空间复杂度是指除了返回的合并后的链表之外的额外空间使用量。

LeetCode运行结果：

方法二：优先队列（Priority Queue）

使用了优先队列来维护当前k个链表中的最小节点。首先，将所有链表的头节点加入到优先队列中。然后，不断从优先队列中取出最小的节点，将其加入到合并后的链表中，并将该节点的下一个节点加入到队列中。重复这个过程直到队列为空。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
public class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }

        // 创建一个优先队列，按照节点值的大小进行排序
        PriorityQueue<ListNode> queue = new PriorityQueue<>((a, b) -> a.val - b.val);

        // 将所有链表的头节点加入到优先队列中
        for (ListNode node : lists) {
            if (node != null) {
                queue.offer(node);
            }
        }

        // 创建一个dummy节点作为合并后的链表头部
        ListNode dummy = new ListNode(0);
        ListNode curr = dummy;

        // 不断从优先队列中取出最小的节点，将其加入到合并后的链表中，然后将该节点的下一个节点加入到队列中
        while (!queue.isEmpty()) {
            ListNode node = queue.poll();
            curr.next = node;
            curr = curr.next;

            if (node.next != null) {
                queue.offer(node.next);
            }
        }

        return dummy.next;
    }
}

复杂度分析：

这个基于优先队列的解法的时间复杂度是O(Nlogk)，其中N是所有链表的节点总数，k是链表的数量。主要的时间消耗在于构建优先队列和从队列中取出最小节点，而构建优先队列的时间复杂度是O(klogk)，每次取出最小节点的操作时间复杂度是O(logk)。由于总共需要取出N个节点，因此总体的时间复杂度是O(Nlogk)。
空间复杂度是O(k)，主要是优先队列所占用的空间。在最坏情况下，优先队列中最多会有k个节点，因此空间复杂度是O(k)。

需要注意的是，这里的空间复杂度是指除了返回的合并后的链表之外的额外空间使用量。

LeetCode运行结果：

方法三：迭代

使用了迭代的方式逐一合并链表。

首先设定一个变量 interval，初始值为1，表示每次合并的链表数量。
然后进行循环，直到 interval 大于等于链表数组的长度。在每次循环中，按照 interval 的步长对链表数组进行逐一合并。每次合并两个链表，将合并结果放回原始数组的相应位置。
通过每次将 interval 值翻倍，循环进行迭代合并，直到 interval 大于等于链表数组的长度，最终得到合并后的链表。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }
        
        int interval = 1;
        while (interval < lists.length) {
            for (int i = 0; i + interval < lists.length; i += 2 * interval) {
                lists[i] = mergeTwoLists(lists[i], lists[i + interval]);
            }
            interval *= 2;
        }
        
        return lists[0];
    }
    
    private ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode curr = dummy;
        
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                curr.next = l1;
                l1 = l1.next;
            } else {
                curr.next = l2;
                l2 = l2.next;
            }
            curr = curr.next;
        }
        
        if (l1 != null) {
            curr.next = l1;
        }
        
        if (l2 != null) {
            curr.next = l2;
        }
        
        return dummy.next;
    }
}

复杂度分析：

时间复杂度：这个解法的时间复杂度是O(Nklogk)，其中N是每个链表的平均长度，k是链表的数量。通过每次将 interval 值翻倍，循环进行迭代合并，直到 interval 大于等于链表数组的长度，最终得到合并后的链表。在每一层循环中的操作总时间复杂度仍然是O(Nk)，因为每一层的合并操作需要遍历所有链表节点。
空间复杂度：这个解法的空间复杂度是O(1)，没有使用额外的数据结构。只需要常数级别的额外空间来保存临时变量。

综上所述，优先队列解法和分治法解法的时间复杂度相同，但优先队列解法的空间复杂度略高于分治法解法。而迭代解法的时间复杂度稍高于前两种解法，并且空间复杂度较低。

LeetCode运行结果：

第三题

题目来源

24. 两两交换链表中的节点 - 力扣（LeetCode）

题目内容

解决方法

方法一：迭代

迭代的思路是遍历链表，每次处理两个相邻节点进行交换。具体步骤如下：

1、定义一个哑节点(dummy)作为新链表的头节点，并将其指向原始链表的头节点head。

2、定义一个指针prev指向哑节点，用于连接新链表中的节点。

3、当原始链表中至少有两个节点时，重复以下操作：

使用指针curr1指向当前要交换的第一个节点，即prev.next。
使用指针curr2指向当前要交换的第二个节点，即curr1.next。
将prev的下一个节点指向curr2，完成节点交换。
将curr1的下一个节点指向curr2的下一个节点，完成节点交换。
将curr2的下一个节点指向curr1，完成节点交换。
更新prev指针和curr1指针，使它们分别指向交换后的第二个节点和下一组要交换的第一个节点。

4、返回哑节点(dummy)的下一个节点作为新链表的头节点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
public ListNode swapPairs(ListNode head) {
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    ListNode prev = dummy;
    
    while (head != null && head.next != null) {
        ListNode curr1 = head;
        ListNode curr2 = head.next;
        
        prev.next = curr2;
        curr1.next = curr2.next;
        curr2.next = curr1;
        
        prev = curr1;
        head = curr1.next;
    }
    
    return dummy.next;
}

}

复杂度分析：

时间复杂度：O(n)，其中n是链表中的节点数。需要遍历链表中的每个节点一次。
空间复杂度：O(1)。只需要常数级别的额外空间。

LeetCode运行结果：

方法二：递归

递归的思路是将链表分成两部分：第一个节点和剩余节点。然后，交换这两部分，并递归地对剩余节点进行两两交换。具体步骤如下：

当链表为空或只有一个节点时，无需交换，直接返回该节点。
令first指向链表的头节点，second指向first的下一个节点。
交换first和second节点，即将second的next指向first，并将first的next指向递归处理剩余节点的结果。
返回second节点作为新链表的头节点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
public ListNode swapPairs(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    
    ListNode first = head;
    ListNode second = head.next;
    
    first.next = swapPairs(second.next);
    second.next = first;
    
    return second;
}
}

复杂度分析：

时间复杂度：O(n)，其中n是链表中的节点数。每次递归都会处理一个节点，并且递归调用的层数最多为n/2。
空间复杂度：O(n)，其中n是链表中的节点数。递归调用的栈空间最多为n/2。

LeetCode运行结果：

方法三：双指针

除了递归和迭代之外，还可以使用双指针的方法来交换链表中的节点。该方法使用两个指针prev和curr分别指向当前要交换的两个节点的前一个节点和第一个节点。通过不断地交换节点，并更新指针，实现链表中节点的两两交换。

注意：它与迭代方法的思路类似，但在细节上有所改动。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
public ListNode swapPairs(ListNode head) {
    // 创建哑节点(dummy)作为新链表的头节点，并将其指向原始链表的头节点head
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    
    // 定义两个指针prev和curr，分别指向当前要交换的两个节点的前一个节点和第一个节点
    ListNode prev = dummy;
    ListNode curr = head;
    
    while (curr != null && curr.next != null) {
        // 获取要交换的两个节点
        ListNode node1 = curr;
        ListNode node2 = curr.next;
        
        // 进行节点交换
        prev.next = node2;
        node1.next = node2.next;
        node2.next = node1;
        
        // 更新prev和curr指针，进行下一组节点交换
        prev = node1;
        curr = node1.next;
    }
    
    return dummy.next;
}

}

复杂度分析：

时间复杂度：O(n) 遍历链表中的每个节点一次，所以时间复杂度是线性的。
空间复杂度：O(1) 只使用了常数级别的额外空间，不随输入规模增加而变化。

LeetCode运行结果：

方法四：栈

除了递归、双指针和迭代之外，还可以使用栈来实现链表节点的两两交换。

这种栈的方法将链表中的节点依次入栈，每次栈中至少有两个节点时，就进行交换操作。通过维护栈来实现链表节点的两两交换。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
public ListNode swapPairs(ListNode head) {
    // 创建一个栈
    Deque<ListNode> stack = new ArrayDeque<>();
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    
    ListNode curr = dummy;
    
    while (curr != null && curr.next != null) {
        // 将当前节点的后继节点和后继的后继节点入栈
        stack.push(curr.next);
        stack.push(curr.next.next);
        
        // 当栈中至少有两个节点时，进行节点交换
        if (stack.size() >= 2) {
            curr.next = stack.pop();
            curr.next.next = stack.pop();
            curr = curr.next.next;
        } else {
            break;
        }
    }
    
    return dummy.next;
}

}

复杂度分析：