⭐ 作者:小胡_不糊涂
🌱 作者主页:小胡_不糊涂的个人主页
📀 收录专栏:浅谈数据结构
💖 持续更文,关注博主少走弯路,谢谢大家支持 💖
时间、空间复杂度
- 1. 算法效率
- 3. 时间复杂度
- 3.1 时间复杂度的概念
- 3.2 大O的渐进表示法
- 3.3 推导大O阶方法
- 3.4 常见时间复杂度计算举例
- 4. 空间复杂度

1. 算法效率
算法效率分析分为两种:第一种是时间效率,第二种是空间效率。
时间效率被称为时间复杂度,而空间效率被称作空间复杂度。
时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间。
在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
3. 时间复杂度
3.1 时间复杂度的概念
时间复杂度的定义: 在计算机科学中,算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间。
一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。
但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
3.2 大O的渐进表示法
试计算下面代码中的 func1 基本操作执行了多少次?
void func1(int N){
int count = 0;
for (int i = 0; i < N ; i++) {
for (int j = 0; j < N ; j++) {
count++;
}
}
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}
Func1 执行的基本操作数为:N* N+2* N+10

- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
3.3 推导大O阶方法
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
- 最坏情况:任意输入规模的最大运行次数(上界)
- 平均情况:任意输入规模的期望运行次数
- 最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
3.4 常见时间复杂度计算举例
实例1:
// 计算func2的时间复杂度?
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}

上述代码的基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)
实例2:
// 计算func3的时间复杂度?
void func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; k++) {
count++;
}
for (int k = 0; k < N ; k++) {
count++;
}
System.out.println(count);
}

上述代码基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
实例3:
// 计算func4的时间复杂度?
void func4(int N) {
int count = 0;
for (int k = 0; k < 100; k++) {
count++;
}
System.out.println(count);
}

上述代码基本操作执行了100次,通过推导大O阶方法,时间复杂度为 O(1)
实例4:
// 计算bubbleSort的时间复杂度?
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}

上述代码基本操作执行最好N次,最坏执行了(N*(N-1))/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N^2)
实例5:
// 计算binarySearch的时间复杂度?
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}
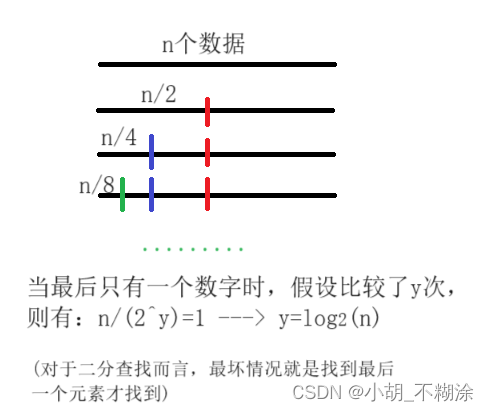
上述代码基本操作执行最好1次,最坏log2(N)次,时间复杂度为 O(log2(N))。
在算法分析中表示是底数为2,对数为N,有些地方会写成lgN。
实例6:
// 计算阶乘递归factorial的时间复杂度?
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N;
}
通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。
实例7:
// 计算斐波那契递归fibonacci的时间复杂度?
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}

通过计算分析发现基本操作递归了2^N 次,时间复杂度为O(2^ N)
4. 空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表法。
实例1:
// 计算bubbleSort的空间复杂度?
void bubbleSort(int[] array){
for (int end = array.length; end > 0; end--) {
boolean sorted = true;//开辟一个空间
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}
使用了常数个额外空间,所以空间复杂度为 O(1)
实例2:
// 计算fibonacci的空间复杂度?
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];//开辟了n个空间
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}
动态开辟了N个空间,空间复杂度为 O(N)
实例3:
// 计算阶乘递归Factorial的空间复杂度?
long factorial(int N) {
return N < 2 ? N : factorial(N-1)*N;
}
递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)