本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

有一个需要密码才能打开的保险箱。密码是 n 位数, 密码的每一位都是范围 [0, k - 1] 中的一个数字。

保险箱有一种特殊的密码校验方法，你可以随意输入密码序列，保险箱会自动记住 最后 n 位输入 ，如果匹配，则能够打开保险箱。

• 例如，正确的密码是 "345" ，并且你输入的是 "012345" ：
  • 输入 0 之后，最后 3 位输入是 "0" ，不正确。
  • 输入 1 之后，最后 3 位输入是 "01" ，不正确。
  • 输入 2 之后，最后 3 位输入是 "012" ，不正确。
  • 输入 3 之后，最后 3 位输入是 "123" ，不正确。
  • 输入 4 之后，最后 3 位输入是 "234" ，不正确。
  • 输入 5 之后，最后 3 位输入是 "345" ，正确，打开保险箱。

在只知道密码位数 n 和范围边界 k 的前提下，请你找出并返回确保在输入的 某个时刻 能够打开保险箱的任一 最短 密码序列 。

示例 1：

输入：n = 1, k = 2
输出："10"
解释：密码只有 1 位，所以输入每一位就可以。"01" 也能够确保打开保险箱。

示例 2：

输入：n = 2, k = 2
输出："01100"
解释：对于每种可能的密码：
- "00" 从第 4 位开始输入。
- "01" 从第 1 位开始输入。
- "10" 从第 3 位开始输入。
- "11" 从第 2 位开始输入。
因此 "01100" 可以确保打开保险箱。"01100"、"10011" 和 "11001" 也可以确保打开保险箱。

提示：

• 1 <= n <= 4
• 1 <= k <= 10
• 1 <= k^n <= 4096

---

保险箱的密码是一个长度为 $n$ 的数字字符串，密码中每位数字的取值范围是从 $0$ 到 $k-1$ 。现在这 $n$ 位密码未知，题目要求我们生成一个可以暴力破解这 $n$ 位密码的字符串序列 $seq$ ，要想用 $seq$ 破解密码，那么 $seq$ 中必须包含 $n$ 位密码的所有组合，最简单的是将 $n$ 位密码的 $k^n$ 个组合拼在一起构成 $seq$ ，但这样的 $seq$ 太长了，题目要我们生成一个包含 $n$ 位密码所有组合情况的一个最短序列。

举个例子，$n=2,k=2$ ，密码长度为 $2$ ，每位数字由 $0$ 和 $1$ 组成，那么长度为 $2$ 的密码就有 $k^n=2^2=4$ 种组合，即 $00,01,10,11$ ，要想破解密码，最简做法是，将这四种密码组合拼在一起组成破解序列 $seq=00011011$ ，这样得到的序列长度为 $8$ ，但它不是包含所有密码组合的最短序列。也就是说这种简单拼接在一起的方法，得到的破解序列是冗余的，会增加破解时间。

而密码破解的方法其实就是朴素的字符串匹配，比如上面的 $seq=00011011$ ，依次匹配的子串是 $00,00,01,11,10,01,11$ ，一共做了 $7$ 次密码匹配，其中 $00,01,11$ 分别匹配了两次，也就是说多做了 $3$ 次冗余的密码匹配。题目要求的 最短破解序列 就是不会产生冗余密码匹配的序列，长度正好是 $k^n+(n-1)$ ，最多只需要匹配 $k^n$ 次，$seq=00110$ 是上面的其中一个破解序列，长度为 $5$ ，依次匹配的子串分别是 $00,01,11,10$ ，匹配的正好是所有四种密码组合。

一种建模方式是：对于所有 $m=k^n$ 个密码组合，我们把每个 $n$ 位可能的密码看成是图中的一个顶点，对于这 $m$ 个顶点构成的 完全图 中，让我们找到这样一个回路 $v_1\to v_2\to v_3\to ...\to v_m\to v_1$ ，除起始顶点外每个顶点访问且仅访问一次，其中 $<u,v>$ 表示回路中一条由顶点 $u$ 指向 $v$ 的边，且顶点 $u$ 长为 $n-1$ 的后缀恰好是顶点 $v$ 的前缀。最终我们要的 最短破解序列 ，一种顶点序列是 $v_1,v_2,v_3,...,v_m$ ，长度为 $k^n+(n-1)$ ，这个 最短破解序列 不止一个，因为 回路 中的任意一个顶点都可以做 起始顶点。这就是 哈密顿回路问题 。

不过查看Wiki，发现本题求的答案有专门的术语 De Bruijn sequence ：$B(k,n)$ 是 $k$ 进制元素构成的循环序列，所有长度为 $n$ 的 $k$ 进制元素序列都是 $B(k,n)$ 的子数组（以环状形式），在 $B(k,n)$ 中出现且仅出现一次。

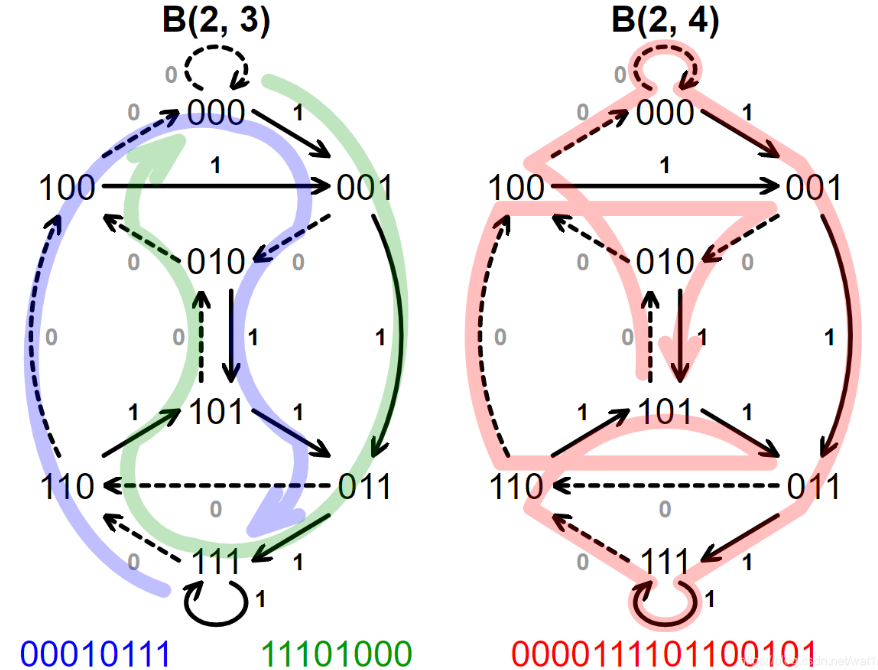
描述该循环序列的图是 De Bruijn 图（一张欧拉图）。使用（$n-1=4-1=3$）3-D De Bruijn 图可以循环构造长度为 $2^4=16$ 的 B(2,4) De Bruijn 序列。如下的3维 De Bruijn 图中的每条边对应于一个四位数字的序列：三个数字分别标记该边要离开的顶点，其后是一个数字标记该边。如果一个人从 $000$ 穿过标记为 $1$ 的边，则一个人到达 $001$ ，从而表明 De Bruijn 序列中存在子序列 $0001$ 。精确遍历每条边一次，就是使用 $16$ 个四位数序列中的每一个恰好一次。下图，在 B(2,3) 中每个顶点被访问一次，而在 B(2,4) 中每条边（包括自环）都被遍历一次。

---

解法 $\text{Hierholzer}$ 算法

$\text{Hierholzer}$ 算法可以在一个欧拉图中找出欧拉回路。具体地，我们将所有的 $n-1$ 位数作为节点，共有 $k^{n-1}$ 个节点，每个节点有 $k$ 条入边和出边。如果当前节点对应的数为 $a_1{a}_2\cdots a_{n-1}$ ，那么它的第 $x$ 条出边就连向数 $a_2\cdots a_{n-1}x$ 对应的节点。这样从一个节点顺着第 $x$ 条边走到另一个节点，就相当于输入了数字 $x$ 。

在某个节点对应的数的末尾放上它某条出边的编号，就形成了一个 $n$ 位数，并且每个节点都能用这样的方式形成 $k$ 个 $n$ 位数。

例如 $k=4,n=3$ 时，节点分别为 $00,01,02,\cdots ,32,33$ ，每个节点的出边的编号分别为 $0,1,2,3$ ，那么 $00$ 和它的出边形成了 $000,001,002,003$ 这 $4$ 个 $3$ 位数，$32$ 和它的出边形成了 $320,321,322,323$ 这 $4$ 个 $3$ 位数。这样共计有 $k^{n-1}\times k=k^n$ 个 $n$ 位数，恰好就是所有可能的密码。

由于这个图的每个节点都有 $k$ 条入边和出边（有向连通图节点度数都为 $0$ ），因此它一定存在一个欧拉回路，即可以从任意一个节点开始，一次性不重复地走完所有的边且回到该节点。因此，我们可以用 $\text{Hierholzer}$ 算法找出这条欧拉回路：

• 设起始节点对应的数为 $u$ ，欧拉回路中每条边的编号为 $x_1,x_2,x_3,\cdots$ ，那么最终的字符串即为 $u{x}_1{x}_2{x}_3\cdots u$

$Hierholzer$ 算法如下：

1. 我们从节点 $u$ 开始，任意地经过还未经过的边，直到我们「无路可走」。此时我们一定回到了节点 $u$ ，这是因为所有节点的入度和出度都相等。
2. 回到节点 $u$ 之后，我们得到了一条从 $u$ 开始到 $u$ 结束的回路，这条回路上仍然有些节点有未经过的出边。从某个这样的节点 $v$ 开始，继续得到一条从 $v$ 开始到 $v$ 结束的回路，再嵌入之前的回路中，即 $$u\to \cdots \to v\to \cdots \to u$$
   变为 $$u\to \cdots \to v\to \cdots \to v\to \cdots \to u$$
3. 以此类推，直到没有节点有未经过的出边，此时我们就找到了一条欧拉回路。

实际的代码编写具有一定的技巧性。

class Solution {
private:
    int highest, k;
    string ans;
    unordered_set<int> rec;
    void dfs(int node) {
        for (int x = 0; x < k; ++x) {
            int nei = node * 10 + x;
            if (!rec.count(nei)) { // 改为插入边
                rec.insert(nei);
                dfs(nei % highest);
                ans += (x + '0');
            }
        }
    }
public:
    string crackSafe(int n, int k) {
        this->highest = pow(10, n - 1);
        this->k = k;
        dfs(0); // 从n-1个0出发
        ans += string(n - 1, '0'); // 返回的路径顺序应该是n-1个0+翻转的ans
        // 由于是欧拉回路,所以不用翻转,即可直接返回
        return ans;
    }
};

但上述写法比较抽象。我们可以这么写：从一个 $n-1$ 长度的全 $0$ 串出发枚举 $k$ 条边，每经过一条边就将其加入到哈希表中，防止重复经过同一条边。

class Solution {
private:
    string ans;
    unordered_set<string> edges;
    void dfs(string &cur, int k) {
        for (int i = 0; i < k; ++i) {
            string edge = cur + to_string(i);
            if (!edges.count(edge)) {
                edges.insert(edge);
                string next = edge.substr(1);
                dfs(next, k);
                ans += to_string(i);
            }
        }
    }
public:
    string crackSafe(int n, int k) {
        string start = string(n - 1, '0');
        dfs(start, k);
        ans += start;
        return ans;
    }
};

复杂度分析：

• 时间复杂度：$O(n\times k^n)$ 。
• 空间复杂度：$O(n\times k^n)$ 。