前言

想要精通算法和SQL的成长之路 - 系列导航

一. 预测赢家

原题链接

主要思路：

1. 我们定义dp[i][j]：在区间 [i, j] 之间先手情况下能拿到的相对分数。
2. 因为玩家1是先手，那么我们站在玩家1的角度来思考，在区间 [i, j] 之间，如果玩家1选择最左侧，值为num[i]。那么玩家2只能在[i-1,j]区间内选择，并且是先手。那么他能拿到的最大相对分数就是：dp[i+1][j]。那么此时玩家1选择左手时的相对分数就是：num[i] - dp[i+1][j] 。
3. 同理如果玩家1先手选择最右侧，那么此时玩家1选择左手时的相对分数就是：num[j] - dp[i][j-1] 。
4. 那么本次玩家1应该选择利益最大化的，即：Max(num[i] - dp[i+1][j], num[j] - dp[i][j-1])。
5. 只要这个值 >=0 （相对分数，差值）玩家1就是胜利者。

代码如下：

public boolean predictTheWinner(int[] nums) {
    return dfs(0, nums.length - 1, nums) >= 0;
}

public int dfs(int left, int right, int[] nums) {
    // 遍历完了，返回0
    if (left > right) {
        return 0;
    }
    // 选择最左侧时的最大相对差值
    int chooseLeft = nums[left] - dfs(left + 1, right, nums);
    // 选择最右侧时的最大相对差值
    int chooseRight = nums[right] - dfs(left, right - 1, nums);
    // 返回最大相对差值
    return Math.max(chooseLeft, chooseRight);
}

当然，这类递归性质的代码，往往都存在一些重复计算的动作，我们用一个全局的数组，来记录递归过程中计算出来的值，即：记忆化搜索。

private int[][] memo;

public boolean predictTheWinner(int[] nums) {
    int len = nums.length;
    memo = new int[len][len];
    // 初始化一个比较特殊的值，用于判断是否计算过
    for (int i = 0; i < len; i++) {
        Arrays.fill(memo[i], Integer.MAX_VALUE);
    }
    return dfs(0, nums.length - 1, nums) >= 0;
}

public int dfs(int left, int right, int[] nums) {
    if (left > right) {
        return 0;
    }
    // 记忆化搜索，如果搜索过，直接返回
    if(memo[left][right] != Integer.MAX_VALUE) {
        return memo[left][right];
    }
    // 如果当前先手，选择左边的数，那么后手就是：dfs(left + 1, right, nums)，计算后手的最大值，我们求此时先后手的相对值
    int chooseLeft = nums[left] - dfs(left + 1, right, nums);
    int chooseRight = nums[right] - dfs(left, right - 1, nums);
    return memo[left][right] = Math.max(chooseLeft, chooseRight);
}

二. 石子游戏（预测赢家的进阶版）

原题链接

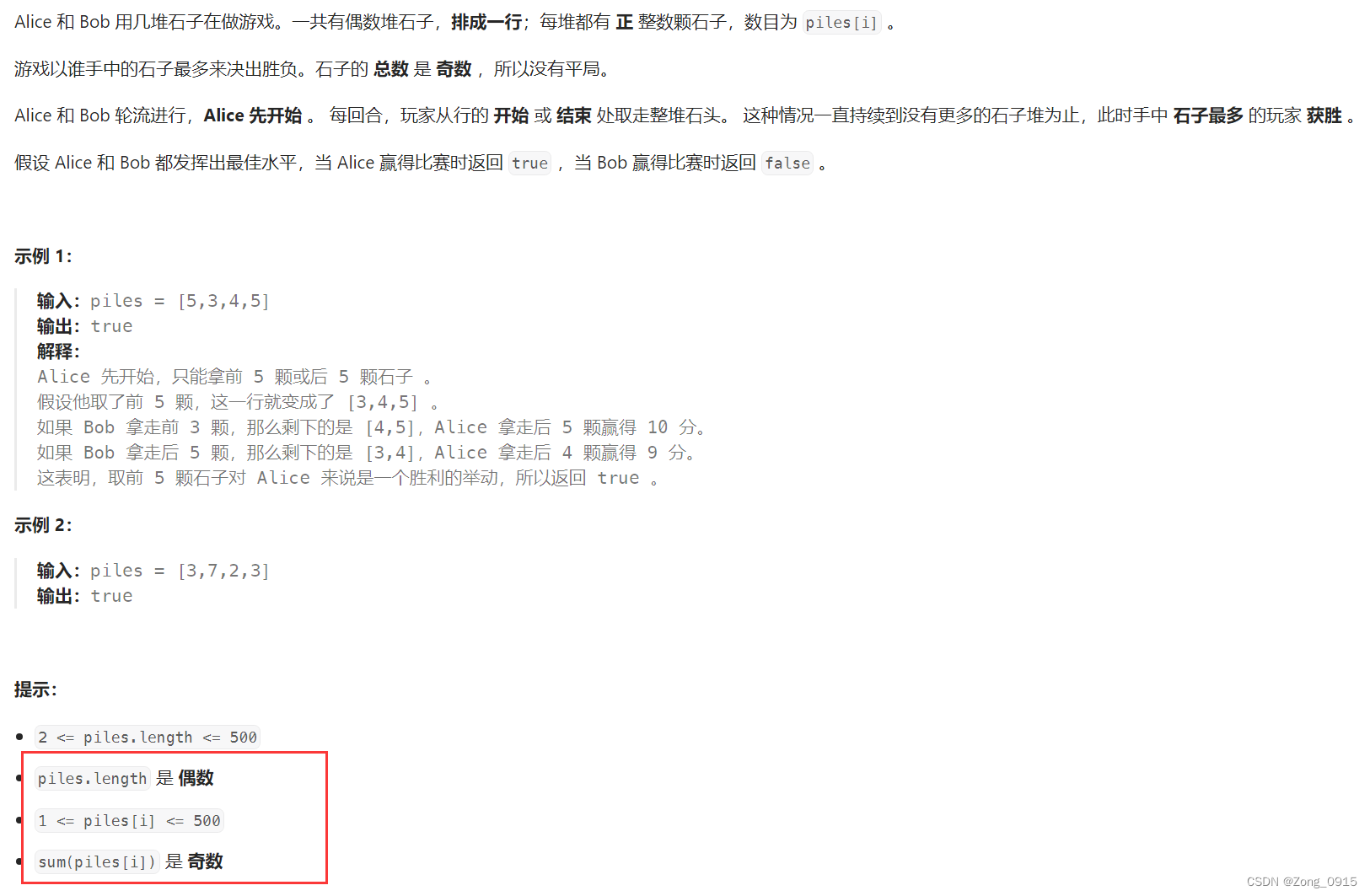
这个题目相当于在第一题的基础上多了两个条件：

• 石头总数为奇数。
• 堆数为偶数。

也就是说不可能存在平局的情况。

2.1 博弈论

在满足上述两个条件的基础上：先手必胜。

我们假设一个数组如下：[奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶]。

• 那么对于先手而言：他能选择的序列为：奇偶序列（头和尾）[奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶]。
• 那么对于后手而言：如果先手选择的是奇数，那么后手选择的序列只能是偶偶序列。[“先手选的”, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶]。反之同理，只能选择奇奇序列。

总之就是：先手必定是奇偶性不同的局面。后手必定是奇偶性相同的局面。

那么问题简单了，我们只需要知道，奇序列的总和 和 偶序列总和 谁大，然后先手每次决策的时候，限制对方只能选择奇偶序列的对立面即可。

因此题目中既然说明了Alice先手的情况，我们直接返回true就完事了。

public boolean stoneGame(int[] piles) {
    return true;
}