飞行动力学 - 第35节-动操纵性 之 基础点摘要
- 1. 动操纵性
- 2. 传递函数
- 3. 动稳定性与动操纵性
- 4. 参考资料
1. 动操纵性
- Free response: x 0 ≠ 0 , u = 0 x_0 \ne 0, u = 0 x0=0,u=0
- Forced response: x 0 = 0 , u ≠ 0 x_0 = 0, u \ne 0 x0=0,u=0
驾驶员操纵飞机的方式有开环与闭环两种。
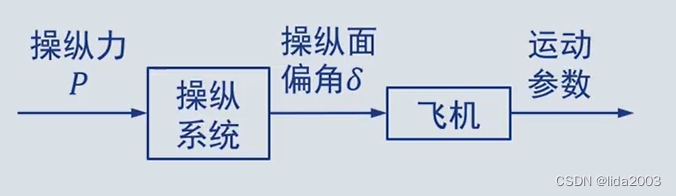
- 开环操纵
不需要精确控制飞机的速度、高度、姿态、航迹的状态/任务;运动参数的变化并不及时响应驾驶员的操纵。
- 闭环操纵
需要精确控制飞机速度、高度、姿态及航迹的状态/任务;通过飞机运动参数的反馈,使驾驶员、操纵系统和飞机三个环节形成闭环回路。
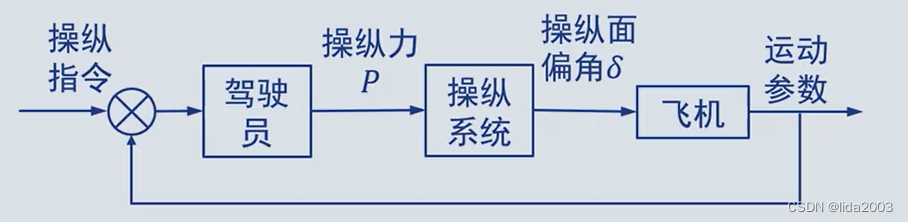
严格的说,整个飞行过程中,驾驶员总是采用闭环操纵方式。但是对于不需要精确操纵的飞行阶段,可近似使用开环操纵方式进行分析。
2. 传递函数
操纵响应分析的核心是传递函数。
对于线性系统,传递函数:初始条件为0时,输出与输入的拉氏变换之比。
x ˙ = A x + B u \dot{x} = A x + B u x˙=Ax+Bu ==> ( s I − A ) x = B u (sI - A)x = B u (sI−A)x=Bu
传递函数矩阵
G ( s ) = ( s I − A ) − 1 B = a d j ( s I − A ) d e t ( s I − A ) B G(s) = (sI - A)^{-1}B = \frac{adj(sI - A)}{det(sI - A)} B G(s)=(sI−A)−1B=det(sI−A)adj(sI−A)B
3. 动稳定性与动操纵性
lim s → 0 G ( s ) = z 1 z 2 … z m p 1 p 2 … p m \lim_{s \to 0}G(s) = \frac{z_1 z_2 \dots z_m}{p_1 p_2 \dots p_m} lims→0G(s)=p1p2…pmz1z2…zm
传递函数的稳态值等于各参数传递函数分子的常数项与分母常数项(所有特征根之积)之比。
对于飞机来说,操纵响应与操纵导数及飞机特征根相关:
- 特征根越大、动稳定度越高,稳态值越小,飞机的响应越迟钝。
- 操纵导数越大、稳态值越大、操纵越灵敏。
4. 参考资料
飞行动力学-第35节-动操纵性