DeepWalk实战---Wiki词条图嵌入可视化

news2024/11/28 14:30:12

DeepWalk是2014年提出的一种Graph中的Node进行Embedding的算法，是首次将自然语言处理领域NLP中的 word2vec拓展到了graph。万事万物皆可embedding，所以DeepWalk我感觉在图机器学习中具有非常强的应用价值。

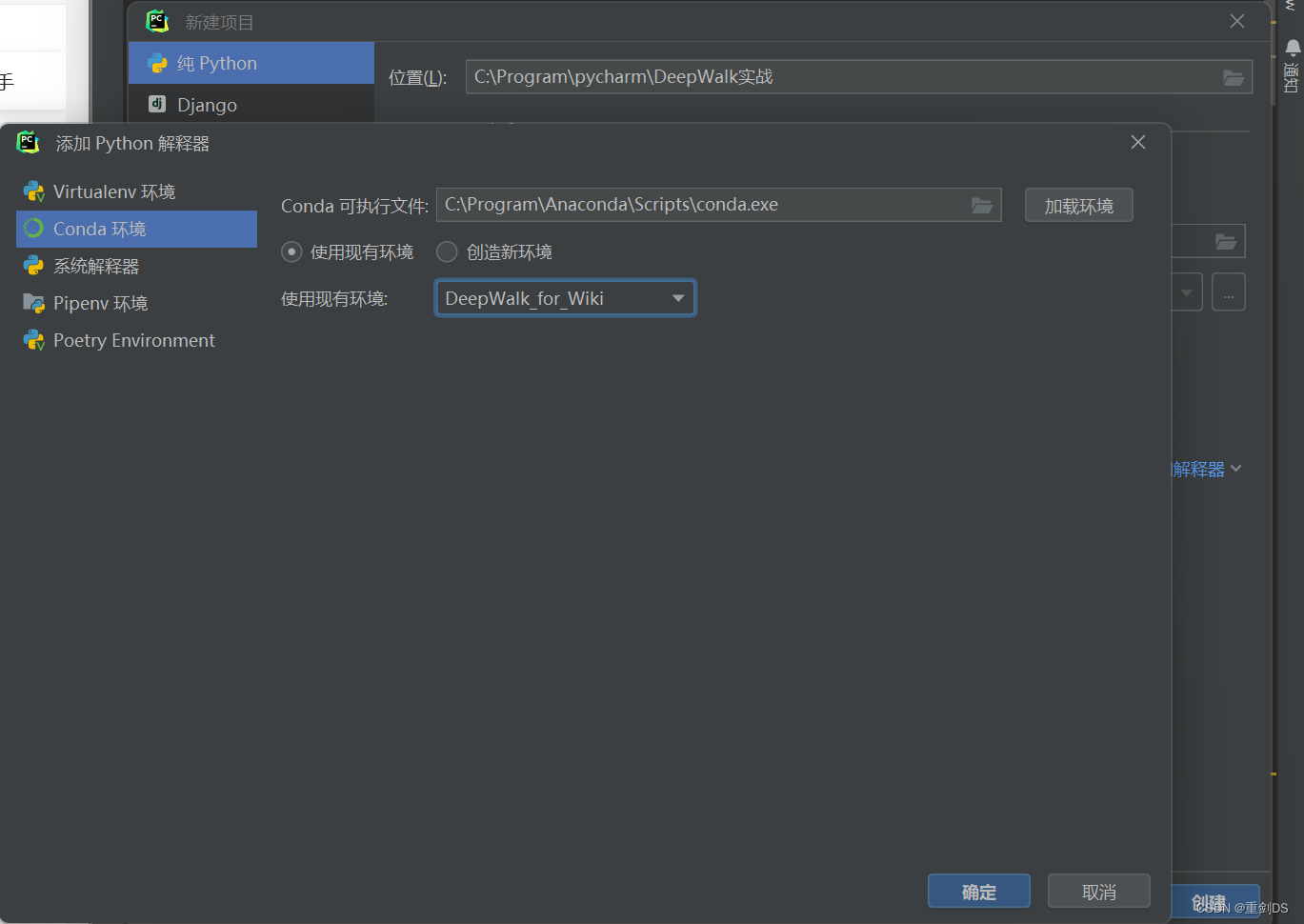
1. 首先打开Anaconda Prompt (Anaconda)，创建一个能用于DeepWalk实战的环境。

2. 在pycharm接着新建项目，导入该环境的解释器

3. 创建好后，安装必要的工具包，gensim是NLP领域的经常要用的工具包，因为DeepWalk其实就是把NLP中的Word2Vec直接用到图上，所以可以直接用NLP领域的工具包gensim。tqdm是进度条工具包，scikit-learn的话是因为要用到降维算法才导入的。matplotlib是可视化用的。

!pip install networkx gensim pandas numpy tqdm scikit-learn matplotlib

4. 在爬虫网站https://densitydesign.github.io/strumentalia-seealsology/

输入从一个链接跳转四个网页，也就是指定Distance设置为4

就会自动画图，

然后爬取1000个网页之后，点击`STOP & CLEAR QUEUE`

接着Download-下载TSV文件，保存至代码相同目录，命名为`seealsology-data.tsv`，csv分割是用逗号，而tsv则是用制表符'\t'。该文件内容如下：

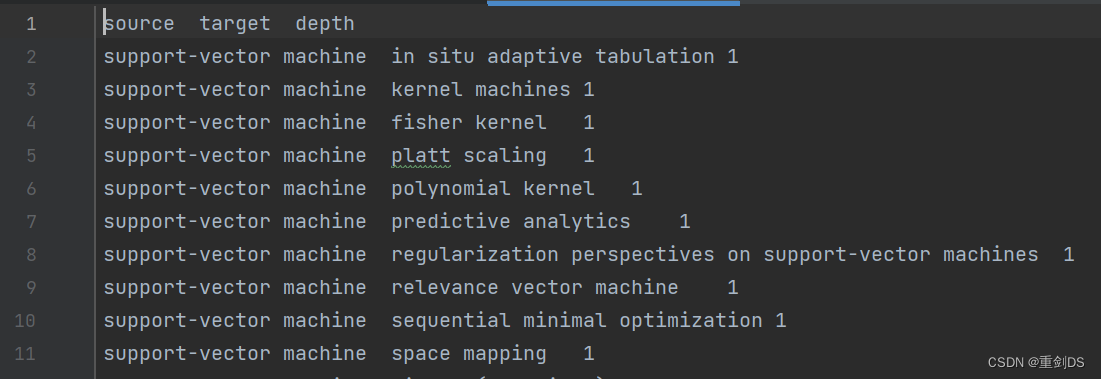
5. 使用read_csv来读取该数据集。

6. 使用network来对上述数据集构造无向图

G = nx.from_pandas_edgelist(df, "source", "target", edge_attr=True, create_using=nx.Graph())

使用len(G)可以发现有8560个node，也就是有8560个词条。

7. 定义并实现一个输入起始点和随机游走步数的函数

def get_randomwalk(node, path_length):
    '''
    输入起始节点和路径长度，生成随机游走节点序列
    '''
    
    random_walk = [node]
    
    for i in range(path_length-1):
        # 汇总邻接节点
        temp = list(G.neighbors(node))
        temp = list(set(temp) - set(random_walk))    
        if len(temp) == 0:
            break
        # 从邻接节点中随机选择下一个节点
        random_node = random.choice(temp)
        random_walk.append(random_node)
        node = random_node
        
    return random_walk

试着从随机森林出发，采样五个节点：

get_randomwalk('random forest', 5)

8. 把所有节点放进一个列表list中。

all_nodes = list(G.nodes())

9. 接下来对每个节点生成随机游走序列，首先设置论文里的那些参数

gamma = 10 # 每个节点作为起始点生成随机游走序列个数
walk_length = 5 
# walk_length 为随机游走序列最大长度
# 可是是无向图喔，length为什么可以小于5呢，不回原路返回吗？答案是不会，看上面get_randomwalk函数的定义，是会排除掉出发点的

10. 对每个结点跑DeepWalk

跑出来的随机游走序列个数如下：

看下索引为1的随机游走序列，其实就是第一个节点的第二趟随机游走序列：

11. 直接用Word2Vec来处理DeepWalk

from gensim.models import Word2Vec # 自然语言处理
model = Word2Vec(vector_size=256, # Embedding维数
                 window=4, # 窗口宽度，NLP中就是左边看四个词，右边看四个词，graph就是左看四节点，右看四节点
                 sg=1, # Skip-Gram，中心节点预测周围4*2节点；为0就是周围节点预测中心节点
                 hs=0, # 不加分层softmax
                 negative=10, # 负采样
                 alpha=0.03,  # 初始学习率
                 min_alpha=0.0007, # 最小学习率
                 seed=14 # 随机数种子
                )

# 用随机游走序列构建词汇表
model.build_vocab(random_walks, progress_per=2)

# 训练，启动
model.train(random_walks, total_examples=model.corpus_count, epochs=50, report_delay=1)

12. 分析Wod2Vec（DeepWalk）结果

查看随机森林的embedding的形状，和11处的vector_size=256一致：

随机森林这一个节点的具体embedding向量如下，完全符合论文中说的那样，embedding是低维（相比起邻接矩阵n*n，已经变小成n*k了，n为节点数量，k为embedding向量长度）、连续（都是大大小小的连续实数）、稠密（向量中无没用的0元素，如one-hot就一大堆0）的向量。

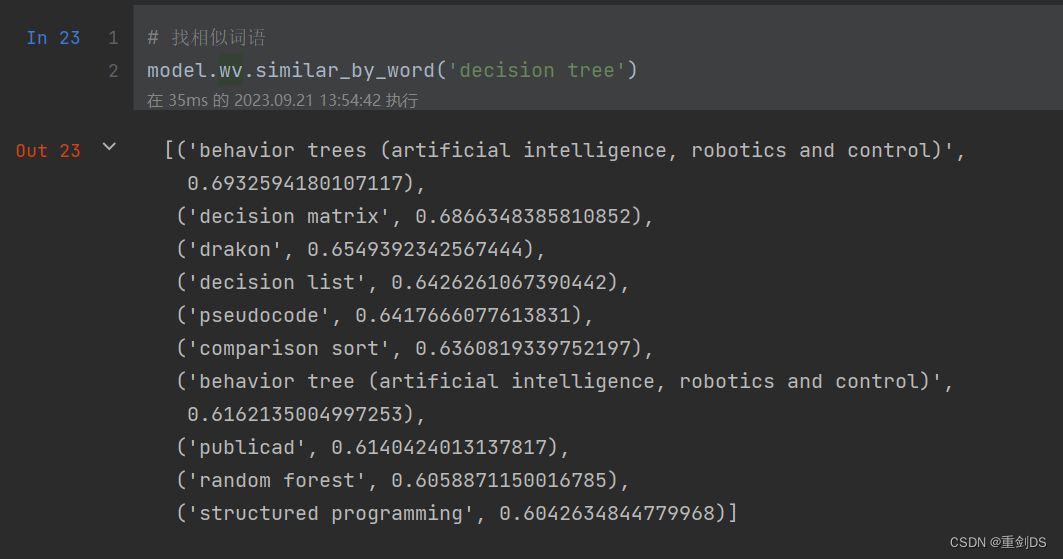
稍稍看看有什么和决策树相似度高的词条（节点）：

13. PCA降维可视化

256维的向量太不直观了，所以我们可以将其降维成2或3维，这样可以直观看到每个node编码后再降维所处的位置。

X = model.wv.vectors

# 将Embedding用PCA降维到2维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
embed_2d = pca.fit_transform(X)

上面的节点都没有打标，我们可视化“计算机视觉”词条的二维embedding↓

term = 'computer vision'
term_256d = model.wv[term].reshape(1,-1)

term_2d = pca.transform(term_256d)

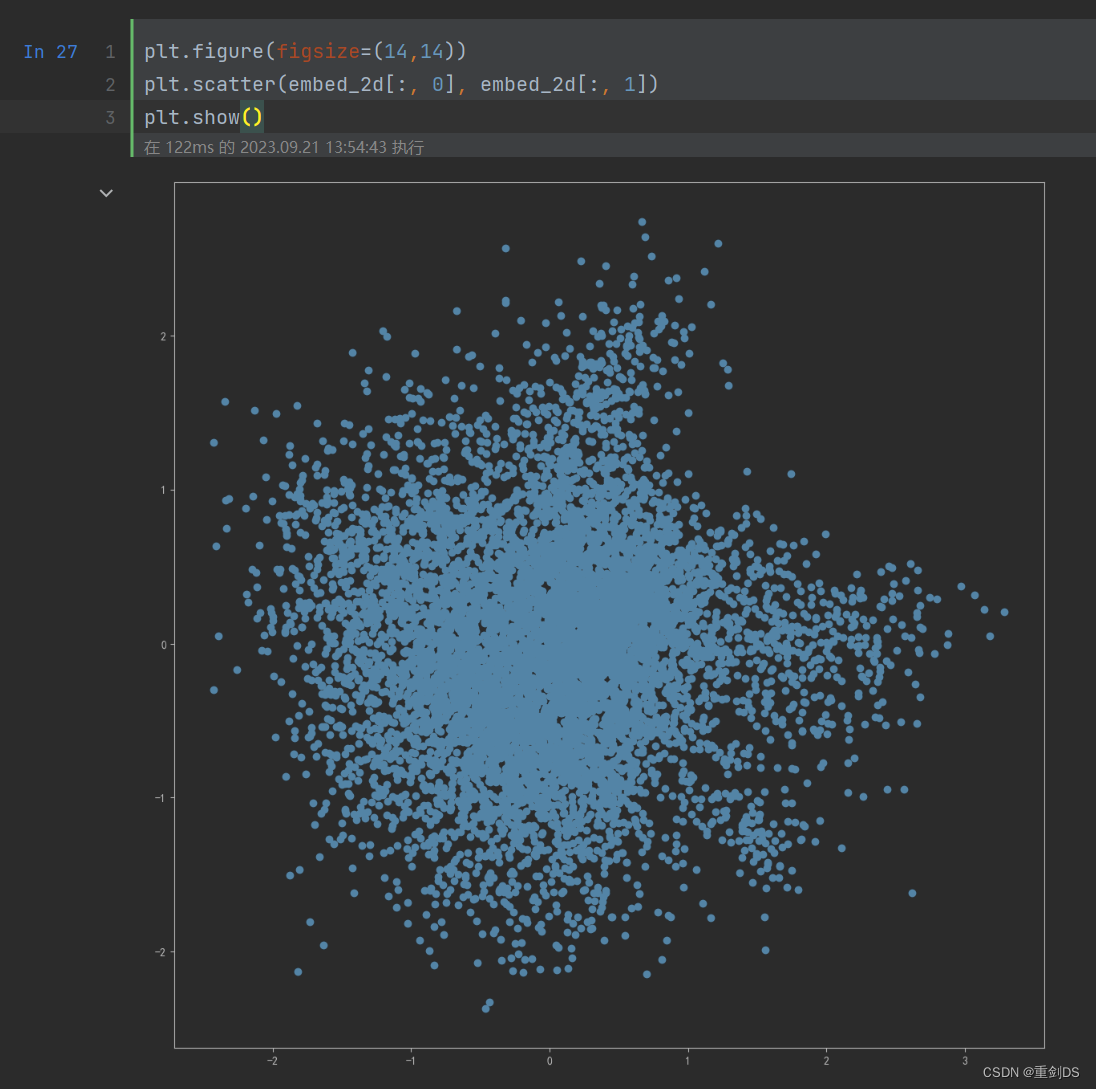
plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:,0], embed_2d[:,1])
plt.scatter(term_2d[:,0],term_2d[:,1],c='r',s=200)
plt.show()

结果如下：

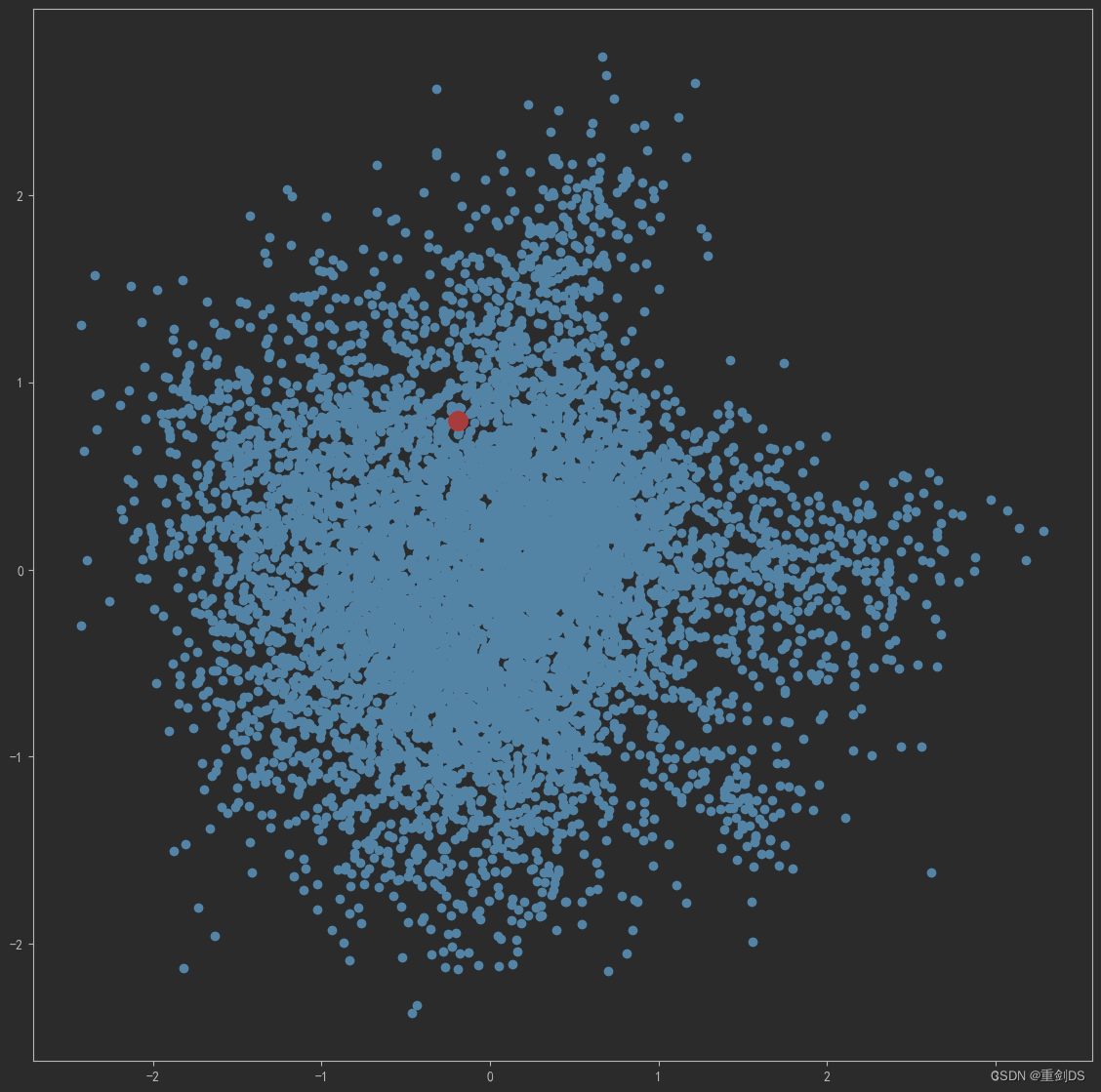
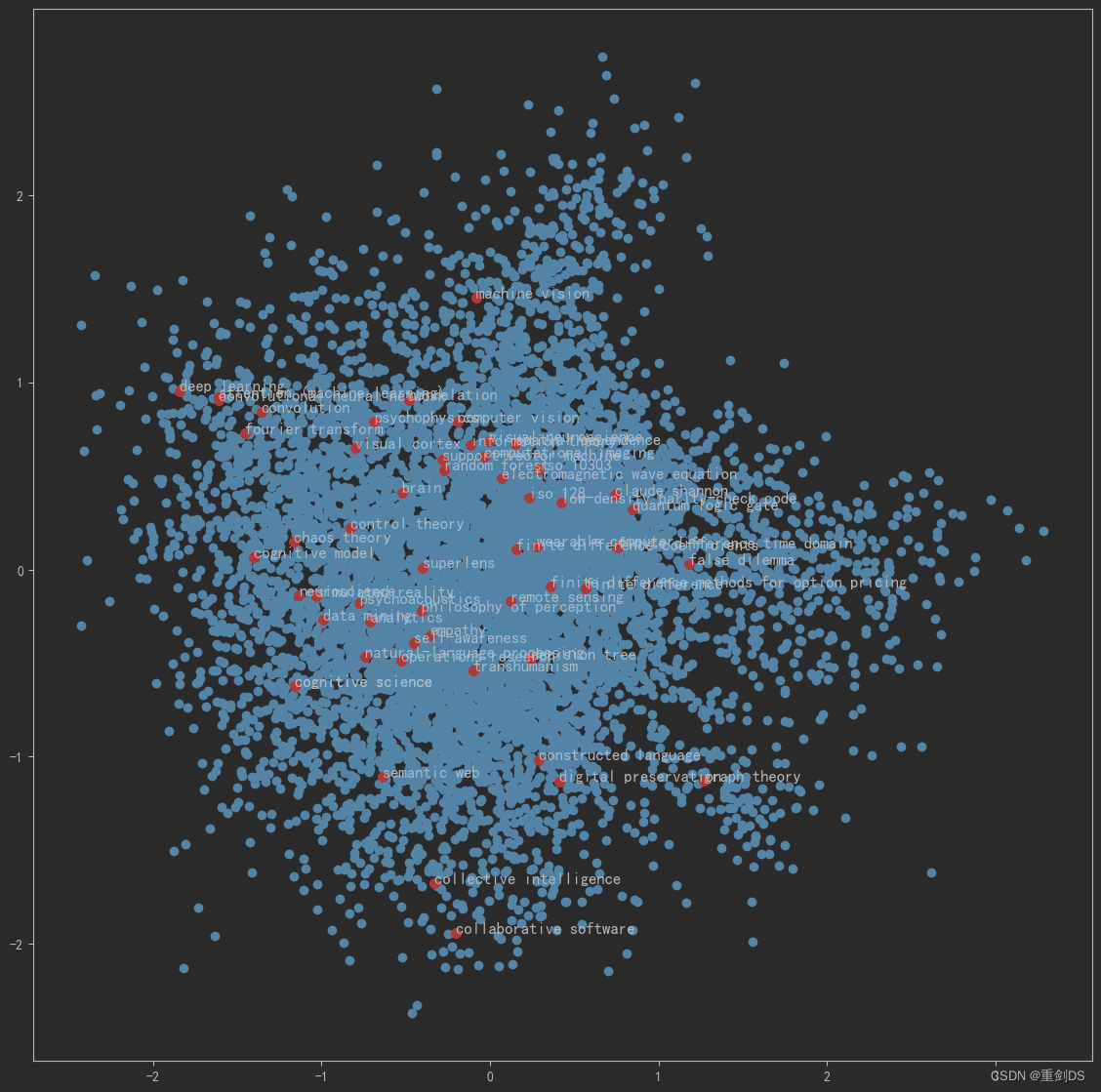
13. 结合PageRank，计算出PageRank节点重要度前三十的节点，再加上一些手动补充我们关心的节点，把这一些节点进行可视化在二维图里。

# 计算PageRank重要度
pagerank = nx.pagerank(G)
# 从高到低排序
node_importance = sorted(pagerank.items(), key=lambda x:x[1], reverse=True)

# 取最高的前n个节点
n = 30
terms_chosen = []
for each in node_importance[:n]:
    terms_chosen.append(each[0])

# 手动补充我们关心的节点
terms_chosen.extend(['computer vision','deep learning','convolutional neural network','convolution','natural-language processing','attention (machine learning)','support-vector machine','decision tree','random forest','computational imaging','machine vision','cognitive science','neuroscience','psychophysics','brain','visual cortex','visual neuroscience','cognitive model','finite difference','finite difference time domain','finite difference coefficients','finite difference methods for option pricing','iso 128','iso 10303'])

# 得到一个转换器term2index ：输入词条，输出词典中的索引号
term2index = model.wv.key_to_index

# 可视化全部词条和关键词条的二维Embedding
plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:,0], embed_2d[:,1])

for item in terms_chosen:
    idx = term2index[item]
    plt.scatter(embed_2d[idx,0], embed_2d[idx,1],c='r',s=50)
    plt.annotate(item, xy=(embed_2d[idx,0], embed_2d[idx,1]),c='k',fontsize=12)
plt.show()

结果如下，不难发现相似的词条节点降维后聚在一起了：

14. PCA是线性降维算法，这里在用下流行的TSNE降维算法

# 将Embedding用TSNE降维到2维
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, n_iter=1000)
embed_2d = tsne.fit_transform(X)

plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.show()

将刚刚的PageRank节点重要度前三十的节点，再加上一些手动补充我们关心的节点再次展示在二维空间直角坐标系中。

plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:,0], embed_2d[:,1])

for item in terms_chosen:
    idx = term2index[item]
    plt.scatter(embed_2d[idx,0], embed_2d[idx,1],c='r',s=50)
    plt.annotate(item, xy=(embed_2d[idx,0], embed_2d[idx,1]),c='k',fontsize=12)
plt.show()