文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
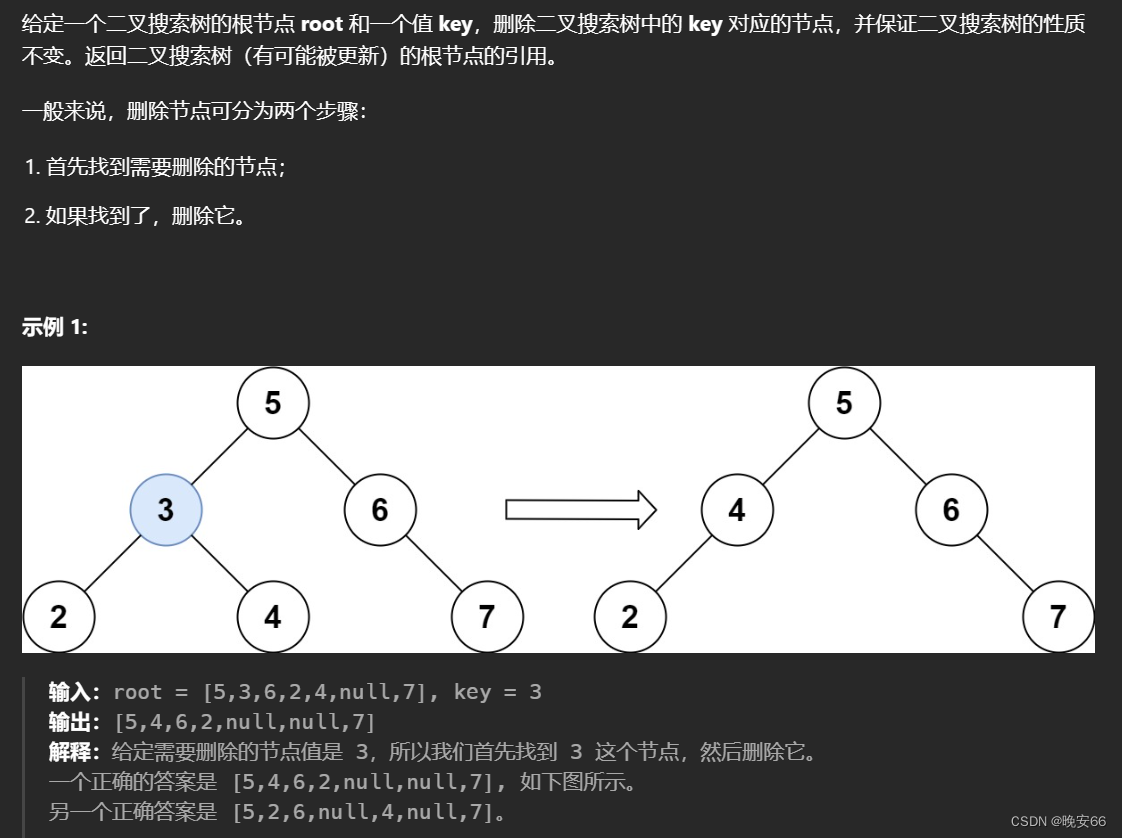

二、解法
思路分析:本题首先要分析删除节点的五种情况:
- 1、没有找到节点
- 2、找到节点
- 左右子树为空
- 左子树为空,右子树不为空
- 右子树为空,左子树不为空
- 左右子树均不为空
程序当中我们选择递归法解题,终止条件中返回一个节点,令上一层递归接住。没有找到节点说明树中没有对应节点的键值,应该是找到空节点的情况。左右子树均为空,说明是叶子节点,返回空节点,并释放空间,上一层中该节点就被置为空节点。左子树不为空,右子树为空,返回左子树即可,反之亦然。左右子树均为不为空的情况比较复杂,因为上一层只接收一个删除后的根节点值,为了使删除后的二叉树仍为二叉搜索树,需要将左右子树合并成一个新的二叉搜索树。那么我们只需将目标节点左子树补位到右子树最底层最左边的节点上,右子树最底层最左边的节点实际上是右子树中键值最小的节点(这个大家可以自己画一个二叉搜索树看看),左子树的值都比这个节点的键值还小,因此需要补位到这个节点的左孩子位置上,伪代码如下,程序当中使用一个while循环寻找右孩子最底层最左边的节点:
右孩子最底层最左边的节点->left = root->left;
auto retNode = root->right;
delete root;
return retNode;
程序如下:
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == NULL) return root; // 没找到节点
if (root->val == key) { // 找到节点
if (root->right == NULL && root->left == NULL) { // 左右孩子均为空,返回空节点
delete root;
return NULL;
}
else if (root->left == NULL) { // 左孩子为空,右孩子不为空,返回右孩子
auto retNode = root->right;
delete root;
return retNode;
}
else if (root->right == NULL) { // 右孩子为空,左孩子不为空,返回左孩子
auto retNode = root->left;
delete root;
return retNode;
}
else { // 左右孩子均不为空,左孩子补位到右孩子最底层最左边的节点上
TreeNode* cur = root->right;
while (cur->left != NULL) {
cur = cur->left;
}
cur->left = root->left;
auto retNode = root->right;
delete root;
return retNode;
}
}
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),最差情况下,寻找和删除个需要遍历一次树。
- 空间复杂度: O ( n ) O(n) O(n),递归的深度最深为 O ( n ) O(n) O(n)。
三、完整代码
# include <iostream>
# include <vector>
# include <string>
# include <queue>
using namespace std;
// 树节点定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == NULL) return root; // 没找到节点
if (root->val == key) { // 找到节点
if (root->right == NULL && root->left == NULL) { // 左右孩子均为空,返回空节点
delete root;
return NULL;
}
else if (root->left == NULL) { // 左孩子为空,右孩子不为空,返回右孩子
auto retNode = root->right;
delete root;
return retNode;
}
else if (root->right == NULL) { // 右孩子为空,左孩子不为空,返回左孩子
auto retNode = root->left;
delete root;
return retNode;
}
else { // 左右孩子均不为空,左孩子补位到右孩子最底层最左边的节点上
TreeNode* cur = root->right;
while (cur->left != NULL) {
cur = cur->left;
}
cur->left = root->left;
auto retNode = root->right;
delete root;
return retNode;
}
}
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};
// 前序遍历迭代法创建二叉树,每次迭代将容器首元素弹出(弹出代码还可以再优化)
void Tree_Generator(vector<string>& t, TreeNode*& node) {
if (!t.size() || t[0] == "NULL") return; // 退出条件
else {
node = new TreeNode(stoi(t[0].c_str())); // 中
if (t.size()) {
t.assign(t.begin() + 1, t.end());
Tree_Generator(t, node->left); // 左
}
if (t.size()) {
t.assign(t.begin() + 1, t.end());
Tree_Generator(t, node->right); // 右
}
}
}
template<typename T>
void my_print(T& v, const string msg)
{
cout << msg << endl;
for (class T::iterator it = v.begin(); it != v.end(); it++) {
cout << *it << ' ';
}
cout << endl;
}
template<class T1, class T2>
void my_print2(T1& v, const string str) {
cout << str << endl;
for (class T1::iterator vit = v.begin(); vit < v.end(); ++vit) {
for (class T2::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {
cout << *it << ' ';
}
cout << endl;
}
}
// 层序遍历
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size(); // size必须固定, que.size()是不断变化的
vector<int> vec;
for (int i = 0; i < size; ++i) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
int main()
{
// 构建二叉树
vector<string> t = { "5", "3", "2", "NULL", "NULL", "4", "NULL", "NULL", "6", "NULL", "7", "NULL", "NULL" }; // 前序遍历
my_print(t, "目标树");
TreeNode* root = new TreeNode();
Tree_Generator(t, root);
vector<vector<int>> tree = levelOrder(root);
my_print2<vector<vector<int>>, vector<int>>(tree, "目标树:");
// 删除目标值
int key = 5;
Solution s;
TreeNode* result = s.deleteNode(root, key);
vector<vector<int>> tree1 = levelOrder(result);
my_print2<vector<vector<int>>, vector<int>>(tree1, "目标树:");
system("pause");
return 0;
}
end