文章目录
- 参数初始化
- 运动模型
- 绝对坐标系
- 以太阳和地球为中心
- 以月球为坐标原点
参数初始化
众所周知,地球围绕太阳转,月球围绕地球转。但在地球上看,月亮和太阳都绕着地球转,那么如果我们是土生土长的月球人,我们看到的是谁绕着谁转呢?
日地月就是典型的三体系统,其中太阳质量为 1.989 × 1 0 30 k g 1.989×10^{30}kg 1.989×1030kg,地球质量为 5.965 × 1 0 24 k g 5.965×10^{24}kg 5.965×1024kg,月球质量为 7.342 ✕ 1 0 22 k g 7.342✕10^{22}kg 7.342✕1022kg,万有引力常数为 G = 6.67 × 1 0 − 11 N ⋅ m 2 / k g 2 G=6.67×10^{-11}N·m2/kg^2 G=6.67×10−11N⋅m2/kg2。地月距离为 3.8 × 1 0 8 m 3.8\times10^8m 3.8×108m;日地距离为 1.5 × 1 0 11 m 1.5\times10^{11}m 1.5×1011m;地球公转速度为 28.8 k m / s 28.8km/s 28.8km/s;月球公转速度为 1 k m / s 1km/s 1km/s,则各参数初始化为
import numpy as np
#后续代码主要更改这里的参数
m = [1.33e20,3.98e14,4.9e12]
x = np.array([0, 1.5e11, 1.5e11+3.8e8])
y = np.array([0.0, 0, 0])
u = np.array([0.0, 0, 0])
v = np.array([0,2.88e4,2.88e4+1.02e3])
运动模型
日地月的运动遵循古老而经典的万有引力
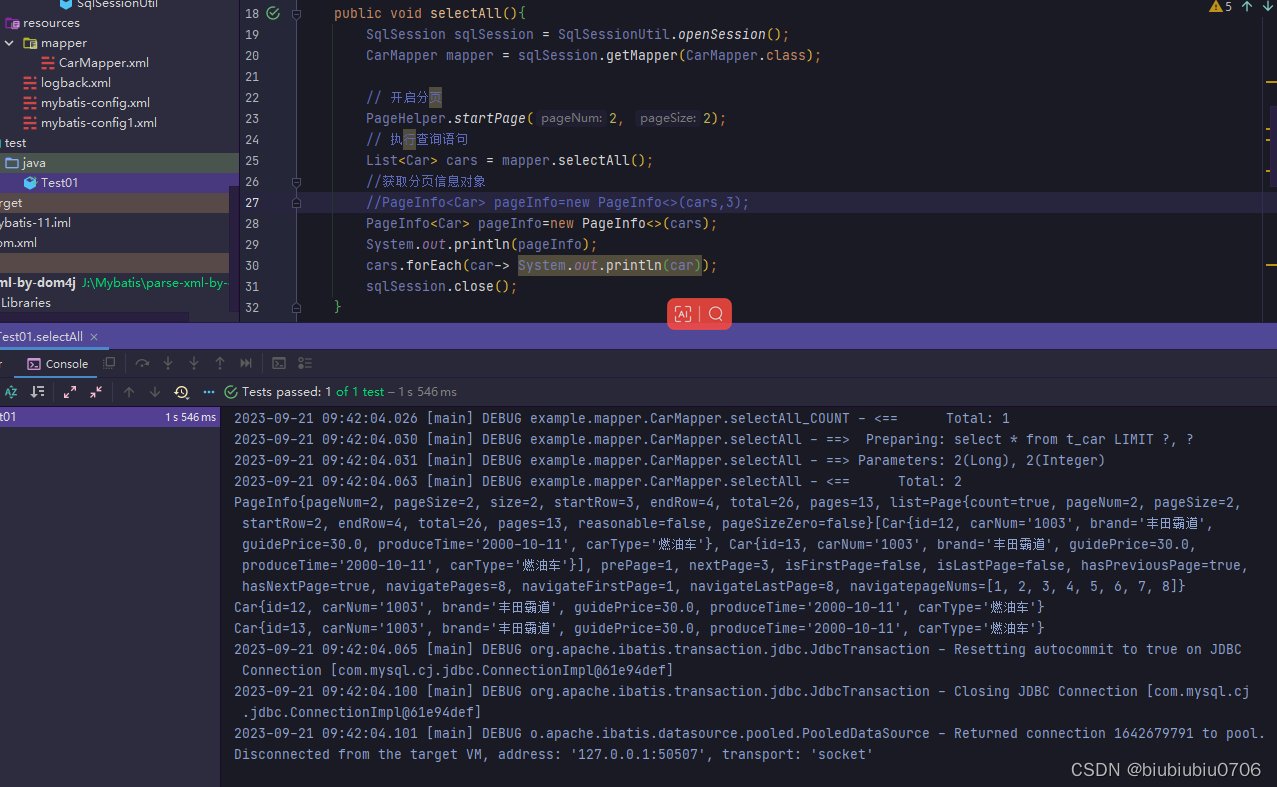
F ⃗ = G m i m j r 2 e ⃗ r \vec F=\frac{Gm_im_j}{r^2}\vec e_r F=r2Gmimjer
然后根据牛顿运动定律
m i d v ⃗ i d t = G m i m j r i j 3 r ⃗ i j , v ⃗ i = d r ⃗ i d t m_i\frac{\text d\vec v_i}{\text dt}=\frac{Gm_im_j}{r_{ij}^3}\vec r_{ij},\quad\vec v_i=\frac{\text d\vec r_i}{\text dt} midtdvi=rij3Gmimjrij,vi=dtdri
写为差分形式
v ⃗ i = ∑ j ≠ i G m j r i j 3 r ⃗ i j d t r ⃗ i = v ⃗ i d t \begin{aligned} \vec v_i&=\sum_{j\not=i}\frac{Gm_j}{r_{ij}^3}\vec r_{ij}\text dt\\ \vec r_i&= \vec v_i\text dt \end{aligned} viri=j=i∑rij3Gmjrijdt=vidt
将其在二维平面坐标系中拆分,令 v ⃗ = ( u , v ) \vec v=(u,v) v=(u,v),则短时间内其变化规则可写为
u i + = ∑ j ≠ i G m j ( x j − x i ) d t ( x i − x j ) 2 + ( y i − y j ) 2 3 v i + = ∑ j ≠ i G m j ( y j − y i ) d t ( x i − x j ) 2 + ( y i − y j ) 2 3 x i + = u ⃗ i d t y i + = v ⃗ i d t \begin{aligned} u_i&+=\sum_{j\not=i}\frac{Gm_j(x_j-x_i)\text dt}{\sqrt{(x_i-x_j)^2+(y_i-y_j)^2}^3}\\ v_i&+=\sum_{j\not=i}\frac{Gm_j(y_j-y_i)\text dt}{\sqrt{(x_i-x_j)^2+(y_i-y_j)^2}^3}\\ x_i&+= \vec u_i\text dt\\ y_i&+= \vec v_i\text dt \end{aligned} uivixiyi+=j=i∑(xi−xj)2+(yi−yj)23Gmj(xj−xi)dt+=j=i∑(xi−xj)2+(yi−yj)23Gmj(yj−yi)dt+=uidt+=vidt
接下来,以太阳为坐标系,做出月亮和地球的运动轨迹
from itertools import product
N = 1000
dt = 36000
ts = np.arange(0,N*dt,dt)/3600/24
xs,ys = [],[]
for _ in ts:
x_ij = (x-x.reshape(3,1))
y_ij = (y-y.reshape(3,1))
r_ij = np.sqrt(x_ij**2+y_ij**2)
for i,j in product(range(3), range(3)):
if i==j : continue
u[i] += (m[j]*x_ij[i,j]*dt/r_ij[i,j]**3)
v[i] += (m[j]*y_ij[i,j]*dt/r_ij[i,j]**3)
x,y = x+u*dt, y+v*dt
xs.append(x.tolist())
ys.append(y.tolist())
xs = np.array(xs)
ys = np.array(ys)
其中,xs和ys都是 N × 3 N\times3 N×3的矩阵,其三列分别代表太阳、地球以及月球的坐标,但地月之间的距离远小于日地间的距离,为了在画图的时候可以看清,所以扩大一百倍
xS, yS = xs[:,0], ys[:,0]
xE, yE = xs[:,1], ys[:,1]
xM = xE + 100*(xs[:,2]-xE)
yM = yE + 100*(ys[:,2]-yE)
绝对坐标系
接下来就是激动人心的时刻,先画出三者在绝对空间中的运动情况
import matplotlib.pyplot as plt
def drawSystem(xS, yS, xE, yE, xM, yM, ax):
ax.plot(xS, yS, marker='o', color='red', label='sun')
ax.plot(xE, yE, color='blue', label='earth')
ax.plot(xM, yM, color='cyan', ls='--', lw=1, label='moon')
plt.legend()
plt.grid()
plt.tight_layout()
ax = plt.subplot()
drawSystem(xS, yS, xE, yE, xM, yM, ax)
plt.show()

以太阳和地球为中心
接下来分别以太阳和地球为坐标原点,绘制其变化
fig = plt.figure()
ax = fig.add_subplot(1,2,1)
drawSystem(xS-xS, yS-yS, xE-xS, yE-yS, xM-xS, yM-yS, ax)
ax = fig.add_subplot(1,2,2)
drawSystem(xS-xE, yS-yE, xE-xE, yE-yE, xM-xE, yM-yE, ax)
plt.show()

左边是以太阳为原点,右边是以地球为原点,所以在地球上看,月亮和太阳都是绕着我们旋转的。
以月球为坐标原点
最后,来看看月球人怎么看这个问题吧
plt.plot(xS-xM, yS-yM, color='red', label='sun')
plt.plot(xE-xM, yE-yM, color='blue', label='earth')
plt.plot(xM-xM, yM-yM, marker='o', color='cyan', label='moon')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()

可以看到,地球是绕着月球转的,而太阳就比较无语了,不知道在外面画什么圈圈。当然,这个图是放大之后的结果,而且月球人需要意识到月亮在自转,否则被地球潮汐锁定的月球,是看不出地球的位置变化的。