前言

 之前我介绍了 二叉搜索树，可看一下博客：C++ - 搜索二叉树_chihiro1122的博客-CSDN博客
二叉搜索树的效率可以达到 O(log n) 。这个复杂度的算法的效率是非常恐怖的，2 的 30 次方大概是 10亿左右。也就是说 如果用暴力查找 需要找 10 亿次，而 最好的效率的二叉搜索树 只用搜索 30 次。是非常恐怖的。

为什么说是 最好效率呢？因为 二叉搜索树有一个弊端，他不是平衡的，在最极端情况下 会退化成类似链表的结构。此时的 时间复杂度就到了 差不多 O(N)了，基本和链表顺序暴力查找没什么区别了 。

所以在上述二叉搜索树的基础之上，为了防止弊端，就有了AVL 树的存在。

关于文章当中的旋转部分的介绍，主要是 左单旋当中最为详细。

AVL树概念 

 AVL树是 二叉平衡搜索树的一种，红黑树也是二叉搜索树的一种，但是两者之间区别很大。

 我们知道，如果一组数据有序或者接近有序，这个可以二叉搜索树会退化成链表的情况，也就是会所单树枝的情况，此时效率相当于是 顺序表的暴力查找。所以，有人就想，如果这棵二叉搜索树的每个结点的高度差不超过1（如果对数当中进行某些操作调整的话），那么这个棵树的 增删查改的时间复杂度就会稳定在 高度次，也就是 O(log N)。

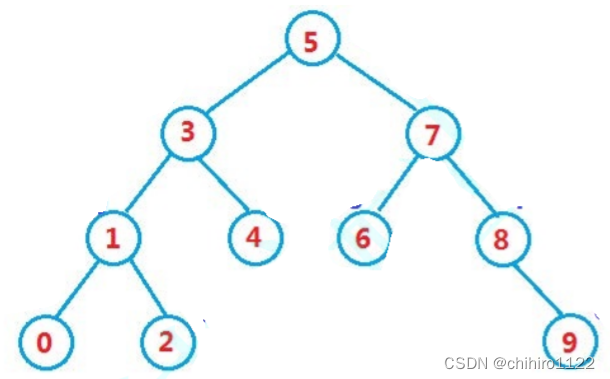
 如上所示就是一个 二叉平衡搜索树，如果我们想构建一个AVL树，方法有很多，这里我们使用 平衡因子 的方式来帮助我们构建这个 AVL树。

首先我们来了解一下什么是 平衡因子。

平衡因子：任何一个结点都有平衡因子，一个结点的平衡因子是 这个结点的 右子树的高度 - 左子树的高度。

  一个 AVL树 或者是 空树，他们都是在二叉搜索树当中多加了以下两个条件：

• 一个结点的左右子树都是 AVL 树
• 每个结点的左右子树高度之差（平衡因子）的绝对值不超过1（1/0/-1）。

 这里 平衡因子不是 0，是因为 如果 平衡因子是 0，那么这棵树就是一个 满二叉树，我们随机插入的结点个数不可能时时都满足 满二茶树的结点个数。比如：树当中只有2 个结点，或者4个结点都不好做到 平衡因子相等。

 AVL树实现

 大体框架

 直接实现 key-value模型的 AVL树；用 pair 类模版来对应存储一个 键值对。

每一个结点上，除了有一个 pair 对象存储键值对，左孩子 右孩子指针之外，还有一个 指向这个结点的父亲的指针。在此 AVL树当中，一个结点有三个链接关系。还有这个结点的 平衡因子 _bf。

template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode* _left;
	AVLTreeNode* _right;
	AVLTreeNode* _parent;

    int _bf;  // 平衡因子

	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
        ,_bf(0)
		()
};

template<class K, class V>
class AVLTree
{
    // 给结点类重命名，方便以后写
	typedef AVLTreeNode<K, V> Node;

	// 构造函数使用默认构造函数

public:
    
    // 成员函数

private:
	Node* _root = nullptr;
};

insert（）插入函数

 insert（）在首次寻找插入位置，和 普通的 二叉搜索树的插入 算法是一样的，只不过在插入之后，要判断对应结点的 平衡因子是否符合要求。同时，对于插入一个结点要影响那些结点的平衡因子，怎么影响，我们在下述当中讨论。

先把首次插入部分写出：
 

	bool insert(const pair<K, V>& kv)
	{
		// 如果当前树为空，直接用头指针只想新结点
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		
		// 不为空接着走
		Node* cur = _root;    // 用于首次插入时候指针的迭代
		Node* parent = _root; 

		while (cur)
		{
			// 如果当前新插入的 key 值比 当前遍历的结点 key 值大
			if (cur->_kv->first < kv.first)
			{
				// 往右迭代器
				parent = cur;
				cur = cur->_right;
			}
			// 反之
			else if (cur->_kv->first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				// 如果相等，就不插入，即插入失败
				return false;
			}
		}

		// 此时已经找到 应该插入的位置
		cur = new Node(kv);
		// 再次判断大小，判断 cur应该插入到 parent 的那一边
		if (parent->_kv->first < kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}

		// 链接 新插入结点 cur 的_parent 指针
		cur->_praent = parent;

		// 利用平衡因子控制平衡
		//·········


		// 插入成功，返回 true
		return true;
	}

现在还有一个问题，是 利用平衡因子来控制 平衡。

平衡因子 控制平衡

我们先来看下述三种情况：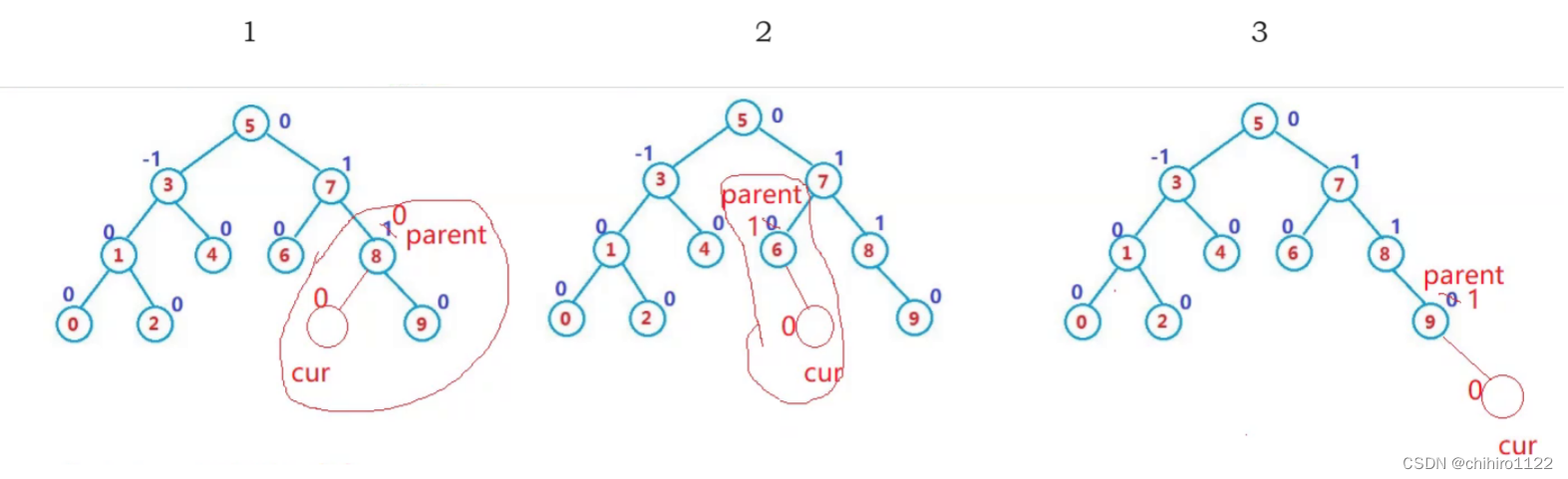

 利用 平衡因子 控制平衡的逻辑：

•  当我们在 parent 的左右两边插入的时候，都有可能会影响 parent 这个结点的 平衡因子，而当 parent 的平衡因子被修改，parent 的 _parent 指针 一直链接到 根结点的 这一个 父类链 都有可能会修改。比如：第二个例子。在 6 的右边插入一个 cur ，6 的平衡因子修改了，同时，cur 的插入，影响到了 7 这个结点的 平衡因子；
• 但是不是一个 结点的 平衡因子 修改了 ，一定会影响其父类结点。
• 我们发现，当在某一个结点的左右孩子插入一个结点之后，这个结点的平衡因子被修改为了 0 ，那么，从这个结点网上链接的 父亲结点，都不会被修改。
•  而且，我们发现，当在 parent 结点的左右孩子插入 cur 之后， parent 结点的 平衡因子 的修改是有规律的，因为 结点的 平衡因子的 计算是 这个结点的 右子树高度 -  左子树高度。
• 所以，当在 parent 的右边插入结点的时候，parent 的平衡因子 ++；当在 parent 的左边插入结点的时候，parent 的平衡因子 --；这个逻辑可以一直用到上述 在 往 root 根结点的 父亲结点的 平衡因子的修改。
•  当 parent 的平衡因子 更新之后，变成0 了，说明这个 parent 的左右子树都平衡了，不会在影响 parent 的父亲了，不用在继续往上更新了。
•  当 parent 结点的平衡因子在修改之后，是 1 或者 -1 ，那么，说明这个 parent 的平衡因子的修改还是会影响到 parent 的父亲结点的 平衡因子，所以还是要继续往上更新。
• 当 parent 结点的 平衡因子 在修改之后，是 2 或者 -2 ，那么，说明 新结点 的插入，影响了 这个 parent 结点的 平衡因子的 有效性，此时 parent 的对应子树已经不是 平衡的了。
•  而且，parent 结点的 平衡因子 在修改之后，是 2 或者 -2，已经失衡了，就不用在网上更新了，因为，此时我们就要对 parent 这颗子树进行旋转，让这个棵子树平衡，当这个子树平衡之后，这颗子树的 父亲也就不需要在 更新 平衡因子了。
•  而且，parent 结点的 平衡因子在更新之后，不能是 3 或者 -3 这些比 2 更大的值，因为如果出现了，就代表在之前 就出现问题，也就是 前面有结点的 平衡因子 已经 被更新为 2 或者 -2 了，这对于上述的逻辑不符。
• 一路往上更新父亲结点的 平衡因子，最多会更新到 root 根结点，如果一直更新到 root 根结点都没有出现 2 或者 -2 的话，那么说明新插入的结点，没有影响任何子树的 平衡因子的有效性。所以，更新到根结点之后就不用再更新了。也就是更新到当前结点的父亲结点为 nullptr 的时候，说明当前结点已经是 根结点了，后续即不用再更新了。
• （此时就可以看出 结点的 _parent 指针的好处了，不仅可以帮助我们往上修改 父亲结点的 平衡因子，还可以帮我们判断是否到达 根结点）

左单旋过程说明 ：

左单旋： cur 为 1 ，parent 为2 就是左单旋。如下图所示：

上述都是在右孩子处插入结点使得平衡失效，所以，我们首先的核心操作是把 这颗不平衡的右子树 移到 左边去，这样才能是实现平衡。

旋转之后要注意的问题：

但是，不能单纯的左移旋转，旋转之后，我们得保证这整棵树还是一个 搜索树，而且这颗树还得是平衡树。

左旋的核心修改步骤：
 

通过上述两个例子我们可以发现，我们要修改修改的是 parent 的平衡因子为 2 或者 -2 的这一刻子树，也就是上图标出的 parent 和 cur 的这一棵子树，对于 parent 和 cur 这两棵链接的结点，左旋就是把 cur 的 左孩子（可能为nullptr）给parent的右孩子，parent 成为 cur 的左孩子，以这种链接关系来实现左旋。

如下就是左单旋核心的代码 ：

parent->_right = cur->_left;
cur->_left = parent;

左单旋向上述做的原因：

实际上， 左单旋完成的事情就是，当前 parent 的平衡因子为2 ，太高了，就把 parent 一下一层，移到 cur 的左孩子处，因为cur 的左孩子不一定为空，所以先要把 cur 的 左孩子 移动到 ，parent 的右孩子处，因为 在移动之前，cur 本来就是 parent 的右孩子；移动之后，parent 的右孩子位置就空出来了。（降低这颗子树的高度）

这个过程一直在做一件事情，保持这棵树是一颗搜索树。我们发现，我们移动的是 parent 的有孩子 ——cur 的左孩子，cur 的左孩子还是在 parent 的右边，只要是在 parent 右边的结点，在搜索树当中都是要比 parent 要大的。

因为上述操作降低这颗子树的高度，所以这颗原本不平衡的子树，现在一下平衡了，那么如果这颗子树有父亲结点，就不需要在工更新这棵子树的 父亲结点的 平衡因子。因为已经平衡了。

左单旋代码实现：

void RotateL(Node* parent)
	{
		Node* cur = parent->_right; // 存储 parent 的右孩子
		Node* curleft = cur->_left; // 存储 cur 的左孩子

		parent->_right = curleft;  
		if (curleft)                // 判断 cur 的左孩子是否为空
		{ 
			curleft->_parent = parent;  // 不为空就 修改 cur 的左孩子的_parent 指针
		}

		cur->_left = parent;
        // 留存一份 根结点指针
		Node* ppnode = parent->_parent;

		parent->_parent = cur;

        // 如果parent 是根结点
		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;

			}

			cur->_parent = ppnode;
		}
        
        // 修改之后 两个结点的 平衡因子都是 0 了
		parent->_bf = cur->_bf = 0;
	}

---

 其实左单旋当中，上述情况都是单一的两个例子，下述才是包含左左-左单旋当中所有的情况。

 左左，左单旋的示意图：

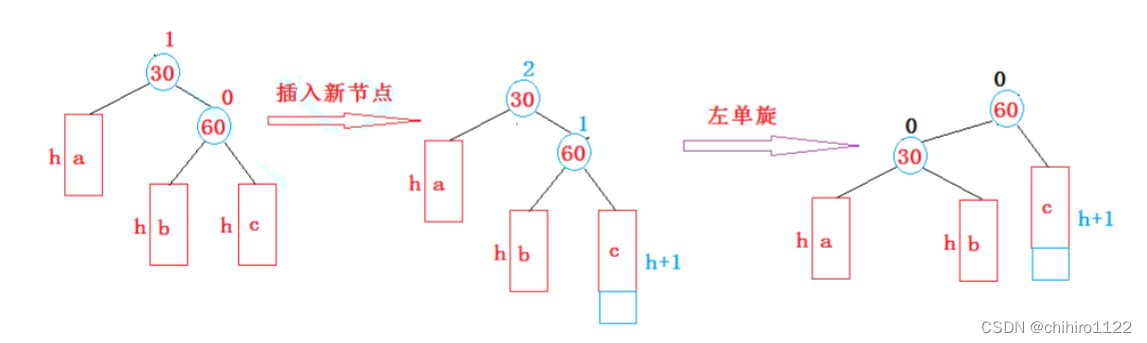
 上述表示，除了 30 和 60 之外，下述的可能是一个孩子，也有可能是一颗子树，当 h == 0 ，或者 h == 1，的情况我们上述的两个单一的例子就已经说明了，

现在我们主要来看 当 h == 2的情况：

当 h >= 2 之后的情况，说明30 和 60 的下面不再是孩子结点，而是一颗子树，而子树就有很多种情况了，比如 当 h == 2 的时候，对于 高度为 2 的子树就有三种情况：
 

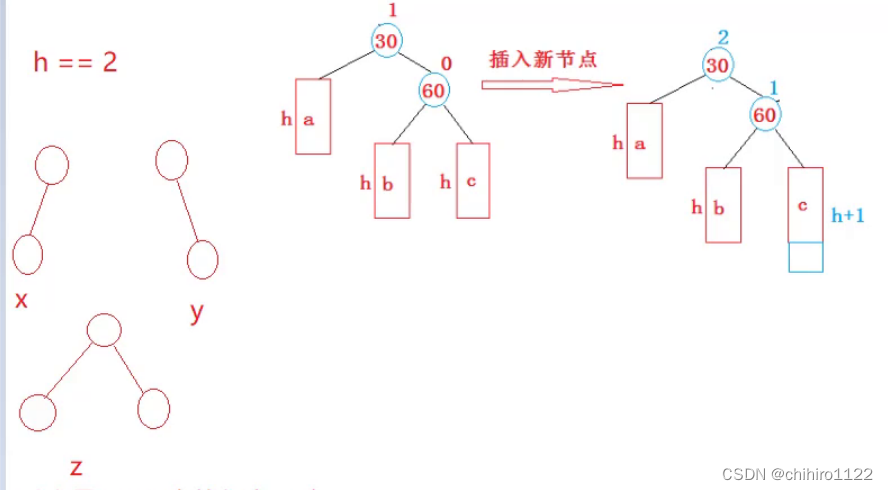
 如上图所示，当h == 2 的时候，对于 a 和 b 两棵子树就有 x/y/z 三种情况；而对于子树 c 就只可能有 z 这一种情况。

因为，假设 c 是 x 或者 y 这两种情况，在插入之前，这颗c子树就已经有点往右边高的倾向了，当在 后序的左边或者右边插入一个结点之后，这颗子树已经不平衡了，不平衡就要发生旋转（逻辑因为是在c子树出插入结点，所以要旋转还是按照左左的方式旋转），而旋转之后，c这颗子树就平衡了。

比如 此时 c 就是 y 这种子树，假设是往子树根结点的左边插入新结点，形成的新的子树就是 z 这种形状的平衡子树，如果是在 根的右孩子的 左右孩子插入结点，那么这棵子树就不平衡了。就要往上更新父亲结点的 平衡因子，当更新到 c 子树的根结点的时候，发现此时 根结点的 平衡因子就不符合规则了，就需要旋转，而旋转之后就是 z 这种 的 子树。

那么，按照上述的逻辑，c子树只能是 z 这种形状的子树，那么当有新的结点的在 c 的后面插入之后，就会引发 c 子树根结点的平衡因子变化，从 0 -> 1。从而就会影响到 整棵树的根结点 30 的平衡因子的变化，1->2，此时就会在 根结点 30 为 paren来旋转。

所以，当 h == 2 的时候，插入之前 这颗数的形状就有 3 * 3 * 1 = 9种；插入新结点的位置就有 4 个位置（即 c 子树的 左右孩子的 左右孩子，总共6中情况）。所以，插入之后 这棵树就有 36 种情况。

我们发现，h == 2 的时候，所引发的情况已经很多了，而且 h 还有 3 4 5 ······等等。

纵使情况很多，但是其实 实现的规则都是一样的，还是按照上述的 左单旋的方式来处理，为什么可以按照上述来处理呢？如下图：

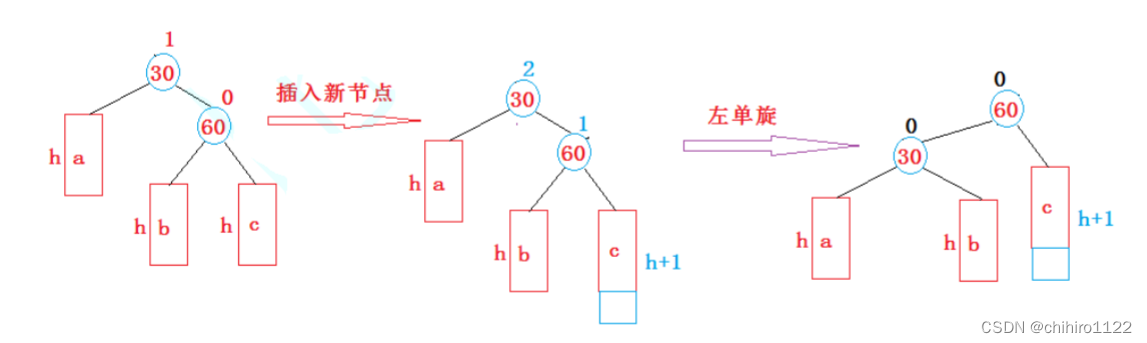
 上述当中， 30 结点的平衡因子已经 == 2了，此时 30 就作为 parent， 60 作为cur，然后来左单旋。 所以就要把 b 这颗子树 给给 30 的右指针，60  的左指针直线 30 ，让 60 作为根结点。

我们为什么可以像上述一样操作呢？因为 b 是已经是一颗 二叉平衡搜索树了，而且 b 其中的结点都比 30 大，都比 60 小，满足作为 30 右子树的条件，加上 30 又满足作为60 的左子树的条件。

 而且修改之后 ，30 和 60 的平衡因子都是 0 ，也就是说 旋转之后，parent 和 cur 两个结点的平衡因子都是 0。

左单旋当中需要注意的问题：

• 上述对左单旋的核心代码做出了说明，但是，实际当中还有一些细节，如果只是用单纯的 核心代码是不能实现左单旋的：
• 除了修改左右孩子的指针，我们使用的是三叉链的结构，还需要修改 parent 和 cur 的_parent 指针。
• 而且，在上述修改 cur 的左孩子的_parent 指针的时候，还需要判断 cur 的左孩子 是否为空，不为空再去修改。
• 我们修改的可能是 parent 位于根结点的，还有可能是 一颗子树，如果是一颗子树，说明在 parent的上面还有结点，而且，在旋转之后，这颗子树的根结点不再是 parent了，而是 cur，cur 的父亲结点应该指向 原本 parent 的 _parent 指针指向的结点。也就是说，我们在修改 parent 的 _parent 指针指向的时候，还需要把 原本 parent 的 _parent 指针指向的结点 留存一份，不然修改之后就找不到了。
• 上述是 parent 的 _parent 指针指向的结点 不为空的情况，也就就是修改的是子树的情况。还有一种情况是 parent 本来就是这整棵树的根结点，此时只需要直接修改 旋转之后 cur 的 _parent指针指向nullptr 就行了。
• 如果 此时 到 parent 和 cur 旋转，就代表着 parent 和 cur 的子树都是 平衡搜索树。

右单旋过程说明：

void RotateR(Node* parent)
	{
		Node* curRight = cur->_right;
		Node* cur = parent->_left;

		parent->_left = curRight;
		if (curLeft)
		{
			curLeft->_parent = parent;
		}

		cur->_right = parent;
		Node* ppnode = parent->_parent;
		parent->_parent = cur;

		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;
			}

			cur->_parent = ppnode;
		}

		parent->_bf = cur->_bf = 0;
	}

右单旋和 左单旋 实现过程其实差不多，两者之间只是旋转的方向不一样，比如之前的 parent 和 cur 的关系是 父亲的 和 右孩子的关系，这个时候如果 父亲的平衡因子 不有效的话就需要左单旋，而 需要右单旋的情况是 cur 是 parent 的左孩子，此时需要右单旋；

右单旋 和 左单旋旋转方式就像是 对称一样，右单旋 就是把cur 的右孩子 给给 parent，然后使得 parent 作为 cur 的右孩子。

右单旋代码实现：

 

 左右双旋 和 右左双旋 的 过程说明：

上述 两个单旋，比如左单旋就是 在parent的右孩子 的 右子树，或者说是在 cur 的 右子树上插入结点才会进行左单旋；在parent的左孩子的左子树，在cur 的左子树上插入结点会进行右单旋。如下所示：

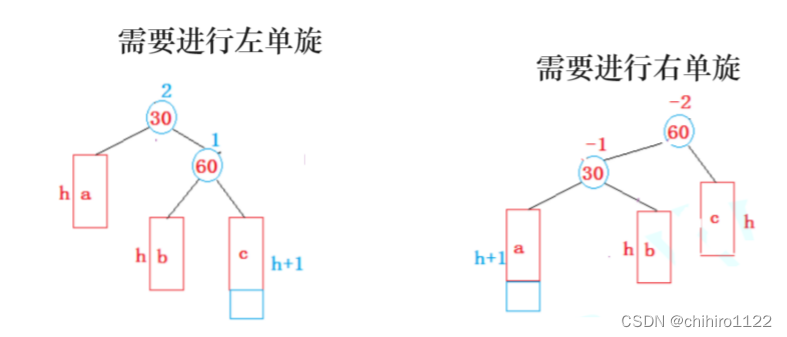
 但是如果反过来，比如 上述左单旋的例子，不在 c 上插入新结点而是在 b 上插入新结点；上述右单旋例子，不在 a 上插入结点，而是在 b 上插入结点；如果只是进行单纯的 左单旋或者 右单旋是不能解决问题的。

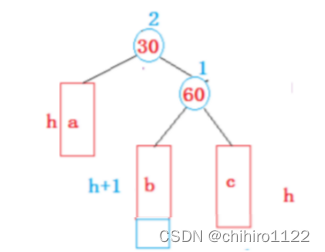
 比如上述，如果只是进行单纯的左单旋之后，变成如下模样：
 

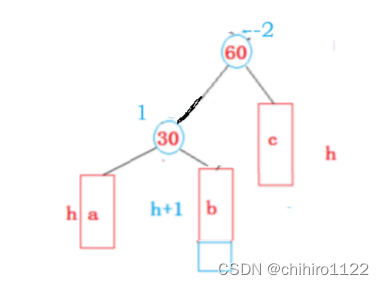
 发现，旋转之后依然是不平衡的。

再看这个例子：

也就是说，此处一次 左单旋是不能解决问题的，插入结点之后 30 的 平衡因子变为了2，我们此时就像使用 左单旋把 30 这颗子树 旋转平衡，就要满足 左单旋的 旋转结构，所以，这里如果我们想使用 左单旋把 30 这颗子树 旋转平衡，就要线使用 右单旋 旋转 60 这颗子树，使得旋转之后，30 这颗子树满足 左单旋的 结构。

当  60 右单旋之后：
 

发现，把60 这颗子树进行右单旋之后， 30 这棵树就满足左单旋的 结构了，此时我们在进行左单旋就可以平衡 30 这颗树：
 

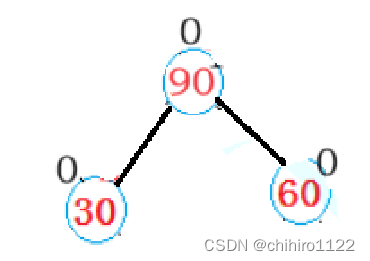
 上述就是 右左双旋的过程，同样的 ，左右双旋 类似，只不过树高的位置不同而已，但是过程完全一样，旋转是对称的。

判断 单旋还是双旋，只需要判断需要旋转的子树是沿着根结点是一条直线还是一条 折现；如果是一条直线，只用单旋就可以解决，如果是一条折现，需要双旋。
 

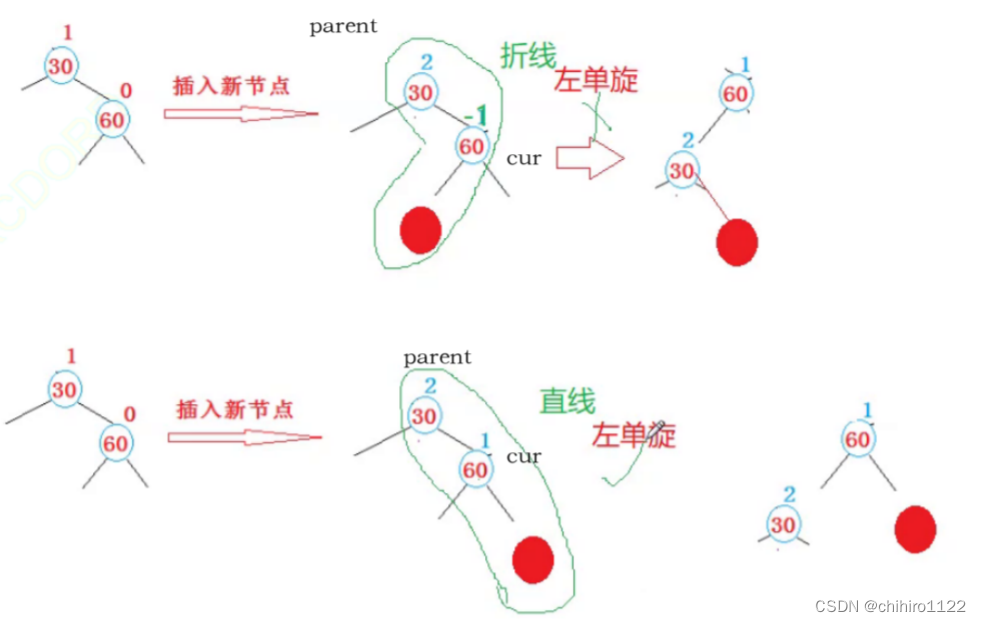
 也就是说：

• 如果 parent 的平衡因子 = 2，cur 的平衡因子 = 1，说明，只是单纯的左边高，只需要进行左单旋；
• 如果 parent 的平衡因子 = -2，cur 的平衡因子 = -1，说明只，只是单纯的右边高，需要进行右单旋；
• 如果 parent 的平衡因子 = 2，cur 的平衡因子 = -1，说明，此时是一条折线 需要进行右左双旋；
• 如果 parent 的平衡因子 = 2，cur 的平衡因子 = 1，说明，此时是一条折线 需要进行左右双旋；

 右左旋转代码：

	//直接复用 左单旋和右单旋
    void RotateRL(Node* praent)
	{
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		int bf = curleft->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 0)       // 平衡因子为 0
		{
			cur->_bf = 0;
			curleft->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == 1)       // 平衡因子为 1
		{
			cur->_bf = 0;
			curleft->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1)       // 平衡因子为 -1
		{
			cur->_bf = 1;
			curleft->_bf = 0;
			parent->_bf = 0;
		}
		else                  // 平衡因子为 不可能为其他值，如果是 ，说明程序写的有问题
		{
			assert(false);
		}
	}

但是，上述只是旋转部分代码。之前说过，单旋之后，parent 和 cur 两个结点的平衡因子一定是 0 ，但是双旋不一样，双旋之后两个结点的 平衡因子不一定是 0 ，而且在分析看来是随机的。

其实双旋的本质是（如上述例子）：

• 把 60 的左边给 30 的右边；
• 把 60 的右边给 90 的左边；
• 60 就成了这颗树的根。

 但是上述是在 60 的左边插入新的结点，如果是在 60 的右边插入结点，结果就不一样了：
 

 我们发现，两种情况再同一双旋当中的位置都不一样。

根据插入位置的不同，旋转之后新结点位置也会不一样，那么就导致不同的插入结果对于 parent 和cur两个结点的平衡因子就有不同的结果。

 那么我们要区分上述两种情况才能解决 平衡因子的问题，我们发现，可以用 60 的平衡因子 来判断 新插入的结点是插入在左孩子还有在右孩子的，如果平衡因子是 1 则在 60 的右孩子位置插入；如果平衡因子是 -1 则在 60 的左孩子位置插入。

 但是，还有一种情况，就是 60 的平衡因子是 0 ，也就是 60 本身就是 新插入的结点的情况也会发生双旋：

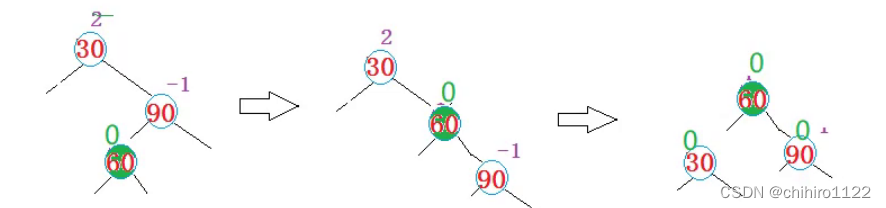
 上述是 h == 1 ；h == 2 的情况，和 单旋一样，h 可能有很多值，但其实也是和 单选一样，都是一样的处理方式：

 如果 h == 0，此时 60 结点就是 新插入的结点；如果 h > 0 就是上图当中一样的模型，有两种方式的插入可以诱发双旋。

• 当在 c 子树当中插入结点，诱发的双旋结果如上，关于 60 30 90 这三个结点的平衡因子 分别是 -1 0 0。
• 当 h == 0 时候，60 30 90 三个结点的 平衡因子 都是 0。
• 当在 b 子树当中插入结点，诱发的双旋结果如喜爱，关于 60 30 90 这三个结点的平衡因子 分别是 0 0 1。

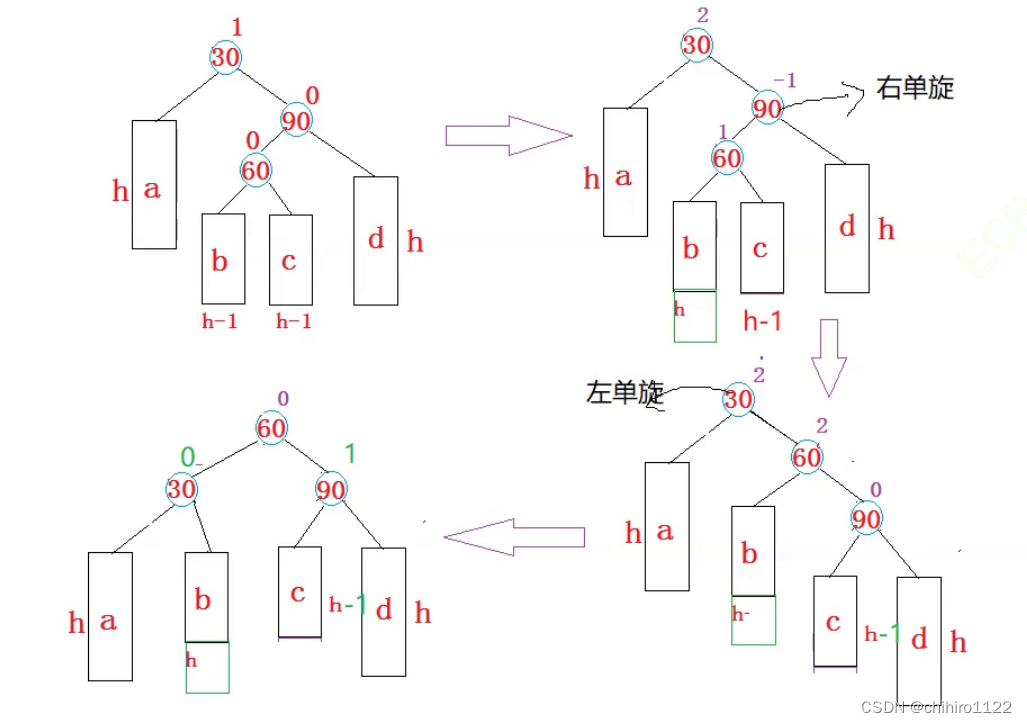
 上述是 b 子树 或者是 c 子树的 高度 从 h -1 变为了h （相当于是插入了结点），所诱发了两种不同的 双旋，而 b 和 c 两个子树的高度不可能同时为 h ，因为，如果 b c 两个子树的 高度同时为 h 的话，60 这个结点的 平衡因子就是 0了，那么当 60 这个 平衡因子已经是 0 就不会在网上更新 平衡因子，也就不会在诱发双旋。

 所以，右左双旋的代码如下：

	//直接复用 左单旋和右单旋
	void RotateRL(Node* praent)
	{
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		int bf = curleft->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 0)       // 平衡因子为 0
		{
			cur->_bf = 0;
			curleft->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == 1)       // 平衡因子为 1
		{
			cur->_bf = 0;
			curleft->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1)       // 平衡因子为 -1
		{
			cur->_bf = 1;
			curleft->_bf = 0;
			parent->_bf = 0;
		}
		else                  // 平衡因子为 不可能为其他值，如果是 ，说明程序写的有问题
		{
			assert(false);
		}
	}

 注意：

• 上述我们在实现单旋函数的时候，其中已经对 两个结点的 平衡因子 修改为0了，那么对于双旋当中，在旋转之后，判断情况修改平衡因子的三种情况当中，就有全部改为 0 的情况，此时有人就问，那么我们在外部是不是可以就不对 全修改为 0 的情况进行修改了呢？
• 如果按照逻辑是哪个来说，可以不修改。但是从耦合上来说，如果不在 双旋函数当中的对 这种情况进行修改，判断修改，那么这个双旋函数就会依赖上 单旋函数的其中的修改规则，如果以后双旋函数像脱离 单旋函数来使用的或者实现的话，那么还得重写对这种情况进行重写。也就是说不写修改0 的话，双旋函数和单旋函数耦合性就变强了。

 对于 左右旋转，和 上述说明的右左旋转是完全类似的，讨论的情况都是一样，要发生 左右旋转，同样是三种情况：

 首先是 60 本来就是 新增的结点；

其次两种是各自在 b 或者 c 子树当中插入结点。

只是旋转方式不同，但是左右双旋和右左双旋两者之间旋转方式是对称的。和 右单旋，左单选一样。

两者的本质都是把 60 的左右子树瓜分在 30 和 90 的下面。30 和 90 分别做了 60 的左右。

对于 左右双旋的 三种情况的判断，同样是判断 60 的平衡因子：

• 是0 的时候，说明此时 60 就是 新增的结点；
• 是1 的时候，说明在 c 子树当中插入，此时 30  60 90 三者的 平衡因子是 -1 0 0
• 是 -1 时候，说是在的 b 子树当中插入，此时 30 60 90 三者的 平衡因子分别是 0 0 1。

具体过程就不画了，过程和 有做双旋当中差不多，按如下图是 在b  子树插入情况示意图：
 

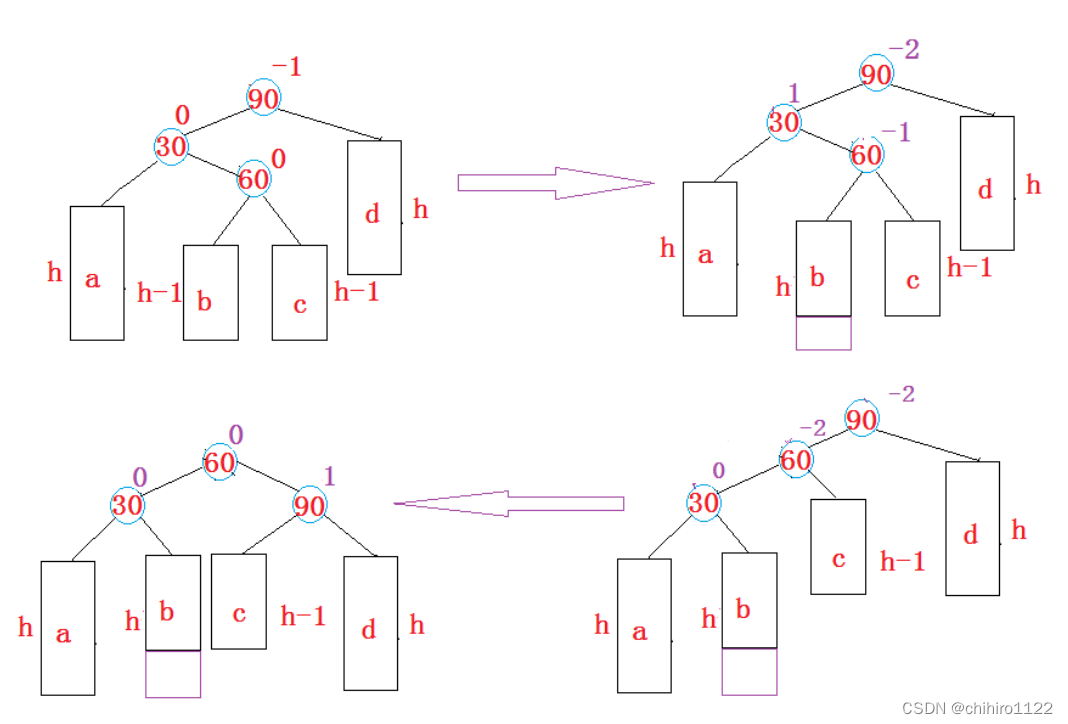
左右双旋 代码实现：

 

void RotateLR(Node* praent)
	{
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		int bf = curleft->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == 0)       // 平衡因子为 0
		{
			cur->_bf = 0;
			curleft->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == 1)       // 平衡因子为 1
		{
			cur->_bf = -1;
			curleft->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == -1)       // 平衡因子为 -1
		{
			cur->_bf = 0;
			curleft->_bf = 0;
			parent->_bf = 1;
		}
		else                  // 平衡因子为 不可能为其他值，如果是 ，说明程序写的有问题
		{
			assert(false);
		}
	}

 

总结旋转

 在旋转过程当中，我们一直强调上述的两个或者是三个结点的平衡因子，而修改的也只是这两三个结点的平衡因子，这是因为每一次遇见不符合规则的 平衡因子的结点只会遇到一个，那么我们就只需要使用 左单旋或者右单旋来平衡这个结点为 根结点的子树，但是，这个子树不一定是 满足左单选 或者 右单旋的结构，所以这时候，在左单旋或者右单旋 之前，还要在 把下面的结构旋转一下，使之构成符合 该子树根结点开始 单旋的结构。

但是在单旋的过程当中，只是对这 两个或者 三个结点进行 链接上是修改，对于他们的 以上所以父亲结点（除 当子树根结点不是 整棵树的根结点时候，需要修改子树根结点和上一个父亲结点链接关系，但是这种情况也只需要修改一个父亲结点的链接关系），还有三个结点的子树，都是整体跟着一起旋转的，不会受到影响。因为父亲的 改变不会影响到 孩子的 平衡因子，孩子的 改变可能会影响到 父亲的 平衡因子。