目录
一、奇异值分解(SVD)
二、Python实现
1. 调包np.linalg.svd()
2. 自定义
三、SVD实现链路预测
一、奇异值分解(SVD)
SVD分解核心思想是通过降低矩阵的秩来提取出最重要的信息,实现数据的降维和去噪。
ChatGPT:
SVD(奇异值分解)是一种常用的矩阵分解方法,它可以将一个矩阵分解为三个矩阵的乘积:U、Σ和V^T。这里,U和V是正交矩阵,Σ是一个对角矩阵。SVD分解的详细过程如下:
假设我们有一个m×n的矩阵A,其中m表示行数,n表示列数。SVD分解的目标是找到三个矩阵U、Σ和V^T,使得:A = UΣV^T
其中,U是一个m×m的正交矩阵,Σ是一个m×n的对角矩阵,V^T是一个n×n的正交矩阵。正交矩阵满足U^TU = I和V^TV = I,其中I是单位矩阵。
对角矩阵Σ的对角线上的元素称为奇异值,通常用σ表示。奇异值按照从大到小的顺序排列,因此可以将它们写成σ₁ ≥ σ₂ ≥ ⋯ ≥ σᵣ,其中r是矩阵A的秩。
SVD分解的步骤如下:
计算矩阵A的转置A^T与A的乘积AA^T,得到一个m×m的对称矩阵。
对对称矩阵AA^T进行特征值分解,得到特征值和对应的特征向量。特征值按照从大到小排列。
根据特征值和特征向量,构造正交矩阵U。U的列向量是对应于AA^T的特征向量,按照特征值从大到小排列。
计算矩阵A的乘积A^TA,得到一个n×n的对称矩阵。
对对称矩阵A^TA进行特征值分解,得到特征值和对应的特征向量。特征值按照从大到小排列。
根据特征值和特征向量,构造正交矩阵V。V的列向量是对应于A^TA的特征向量,按照特征值从大到小排列。
从特征值中计算奇异值,奇异值的平方根即为特征值的平方根。
根据奇异值构造对角矩阵Σ。
最后,将矩阵A分解为A = UΣV^T。
二、Python实现
1. 调包np.linalg.svd()
在Python中,可以使用NumPy库来实现SVD分解。以下是一个示例代码:
import numpy as np
# 定义一个矩阵A
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 使用NumPy的svd函数进行SVD分解
U, s, Vt = np.linalg.svd(A)
# 打印分解结果
print("矩阵U:")
print(U)
print("奇异值:")
print(s)
print("矩阵V的转置:")
print(Vt)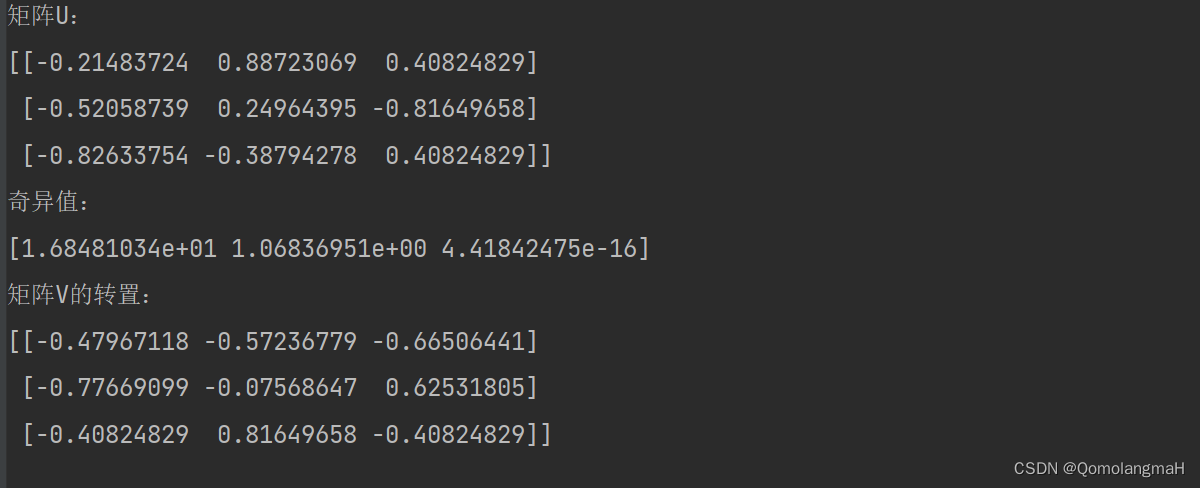
运行上述代码,将得到矩阵A的SVD分解结果。其中,U是一个正交矩阵,s是包含矩阵A的奇异值的一维数组,Vt是V的转置矩阵。
2. 自定义
import numpy as np
def svd_decomposition(A):
# 计算 A 的转置与 A 的乘积
AAT = np.dot(A, A.T)
# 计算 A 的乘积与 A 的转置的乘积
ATA = np.dot(A.T, A)
# 计算 A 的转置与 A 的乘积的特征值和特征向量
eigenvalues_U, eigenvectors_U = np.linalg.eig(AAT)
# 计算 A 的乘积与 A 的转置的特征值和特征向量
eigenvalues_V, eigenvectors_V = np.linalg.eig(ATA)
# 对特征值进行排序,并获取排序索引
sorted_indices_U = np.argsort(eigenvalues_U)[::-1]
sorted_indices_V = np.argsort(eigenvalues_V)[::-1]
# 获取奇异值
singular_values = np.sqrt(np.sort(eigenvalues_U)[::-1])
# 获取 U 矩阵
U = eigenvectors_U[:, sorted_indices_U]
# 获取 V 矩阵
V = eigenvectors_V[:, sorted_indices_V]
# 对 V 进行转置
V = V.T
return U, singular_values, V
# 定义一个矩阵 A
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 调用自定义的 SVD 分解函数
U, s, Vt = svd_decomposition(A)
# 打印分解结果
print("矩阵 U:")
print(U)
print("奇异值:")
print(s)
print("矩阵 V 的转置:")
print(Vt) 自定义的 svd_decomposition 函数基于奇异值分解算法,通过计算矩阵 A 的转置与 A 的乘积以及 A 的乘积与 A 的转置的特征值和特征向量来实现 SVD 分解。
三、SVD实现链路预测
import numpy as np
# 定义邻接矩阵A,表示网络结构
A = np.array([[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]])
# 进行奇异值分解
U, S, V = np.linalg.svd(A)
# 选择保留的前k个奇异值和对应的奇异向量
k = 2 # 选择保留的奇异值个数
U_k = U[:, :k]
S_k = np.diag(S[:k])
V_k = V[:k, :]
# 进行链路预测
A_pred = U_k @ S_k @ V_k
# 保留两位小数
A_pred = np.round(A_pred, decimals=2)
# 输出链路预测结果
print("链路预测结果:")
print(A_pred) 首先定义了一个邻接矩阵 A,然后使用 np.linalg.svd 函数进行奇异值分解。然后,我们选择保留前 k 个奇异值和对应的奇异向量(在示例中选择 k=2),并重新构造预测的邻接矩阵 A_pred。最后,输出链路预测的结果。