我们知道数据的存储结构分为线性与非线性。线性就是1对1的结构，像栈与队列都属于线性结构。那什么是非线性的结构呢？
非线性即1对n的结构这更符合常规情况，线性结构本质上属于非线性结构中的一种特殊形式，像树就属于非线性结构。但是树并不适合编码操作，需要将其转为二叉树，既然二叉树是一种数据存储的结构，那就涉及到数据遍历的问题。有关二叉树的遍历有三种方式，即先序遍历、中序遍历与后续遍历。
本篇参考博文C++实现二叉树的递归遍历(详细步骤与代码实现)进行补充后进行介绍。

1. 二叉树遍历基本概念

1. 1 遍历定义

指按某条搜索路线遍访每个结点且不重复(又称周游)。

1. 2 遍历用途

它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心

1. 3 遍历方法

牢记一种约定，对每个结点的查看都是“先左后右”，区别是访问根、左、右的顺序。
限定先左后右，树的遍历有三种实现方案：
DLR（先序遍历、根左右） 、 LDR （中序遍历、左根右） 、 LRD（后续遍历、左右根）

具体的遍历方法为：

• DLR 一 先序遍历，即先根再左再右
• LDR 一 中序遍历，即先左再根再右
• LRD 一 后序遍历，即先左再右再根

注：“先、中、后”的意思是指访问的结点 D 是先于子树出现还是后于子树出现。
从递归的角度看，这三种算法是完全相同的，或者说这三种遍历算法的访问路径是相同的，只是访问结点的时机不同。

技巧总结：先分析是否为一个树，是树就按照上述先什么后什么的顺序进行遍历

2. 二叉树的遍历举例

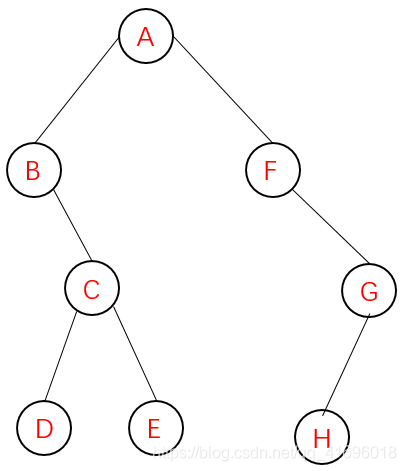
根据以下二叉树简单谈一下何为先序遍历、中序遍历与后序遍历：

2.1 先序遍历（DLR）

先从顶部二叉树节点A开始遍历，输出A——>寻找节点A的左子树，找到B，输出B，B为一个树继续遍历——>寻找节点B的左子树，没找到——>寻找节点B的右子树，找到节点C输出C，C为一个树继续遍历——>寻找节点C的左子树，找到D输出D，D不是一个树——>寻找节点C的右子树，找到E输出E，E不是一个树。

顶点A节点的左子树完全访问完毕，现在访问节点A的右子树，找到F输出F，F为一个树继续遍历——>寻找节点F的左子树，没找到——>寻找节点F的右子树，找到G输出G，G为一个树继续遍历——>寻找节点G左子树，找到H直接输出，H不是一个树——>寻找节点G右子树，没找到——>遍历完成，结束。

遍历结果为：ABCDEFGH

2.2 中序遍历（LDR）

先从顶部节点A开始——>寻找左子树，找到B，B为一个树——>寻找B节点左子树，没找到——>输出B——>寻找B节点右子树，找到C，C为一个树——>寻找C节点左子树，找到D，D不是一个树，输出D——>输出C——>寻找C节点右子树，找到E，E不是一个树，输出E。

A的左子树访问完毕——>输出A——>寻找节点A的右子树，找到F，F为一个树继续遍历——>寻找节点F的左子树，没找到——>输出F——>寻找节点F的右子树，找到G，G为一个树继续遍历——>寻找节点G的左子树，找到H，H不是一个树——>输出G——>寻找G的右子树，没找到——>遍历完成，结束。

遍历结果为：BDCEAFHC

2.3 后序遍历（LRD）

先从顶部节点A开始——>寻找左子树，找到B，B为一个树——>寻找B节点左子树，没找到——>寻找B节点右子树，找到C，C为一个树——>寻找节点C的左子树，找到D，D不是一个树直接输出——>寻找节点C右子树，找到E，E不是一个树直接输出——>输出节点C-——>输出节点B.

A的左子树访问完成，寻找A的右子树，找到F，F为一个树——>寻找节点F的左子树，没找到——>寻找节点F的右子树，找到G，G为一个树——>寻找节点G的左子树，找到G,H不是一个树直接输出——>寻找节点G右子树，没找到——>输出G——>输出F——>输出A——>遍历完成，结束。

遍历结果为：DECBHGFA

3. 二叉树三种遍历方法代码实现

3.1 先定义二叉树节点

//定义二叉树节点
class binarynode
{
public:
	char ch;			 //节点数据域
	binarynode* lchild;  //左孩子
	binarynode* rchild;  //右孩子
};

3.2 三种遍历方式

//递归遍历
//先序
void recursion_dlr(binarynode* root)
{
	if (root==NULL)
	{
		return;
	}
	//遍历根节点
	cout<<root->ch<<"\t";
	//遍历左子树
	recursion_dlr(root->lchild);
	//遍历右子树
	recursion_dlr(root->rchild);
}
//中序
void recursion_ldr(binarynode* root)
{
	if (root==NULL)
	{
		return;
	}
	//遍历左子树
	recursion_ldr(root->lchild);
	//遍历根节点
	cout<<root->ch<<"\t";
	//遍历右子树
	recursion_ldr(root->rchild);
}
//后序
void recursion_lrd(binarynode* root)
{
	if (root==NULL)
	{
		return;
	}
	//遍历左子树
	recursion_lrd(root->lchild);
	//遍历右子树
	recursion_lrd(root->rchild);
	//遍历根节点
	cout<<root->ch<<"\t";
}

3.3 创建案例中的二叉树

//创建二叉树
void createtree()
{
	//创建节点
	binarynode node1={'A',NULL,NULL};
	binarynode node2={'B',NULL,NULL};
	binarynode node3={'C',NULL,NULL};
	binarynode node4={'D',NULL,NULL};
	binarynode node5={'E',NULL,NULL};
	binarynode node6={'F',NULL,NULL};
	binarynode node7={'G',NULL,NULL};
	binarynode node8={'H',NULL,NULL};
	//建立节点关系
	node1.lchild=&node2;
	node1.rchild=&node6;
	node2.rchild=&node3;
	node3.lchild=&node4;
	node3.rchild=&node5;
	node6.rchild=&node7;
	node7.lchild=&node8;
	cout<<"先序遍历："<<endl;
	recursion_dlr(&node1);
	cout<<endl;
	cout<<"中序遍历："<<endl;
	recursion_ldr(&node1);
	cout<<endl;
	cout<<"后序遍历："<<endl;
	recursion_lrd(&node1);
	cout<<endl;
}

3.4 遍历结果

int main()
{
	createtree();
	system("pause");
	return 0;
}

4. 视频学习地址：二叉树的递归遍历