什么是HTTPS

和HTTP一样也是应用层协议,但在HTTP协议的基础上引入了一个加密层(SSL/TLS).
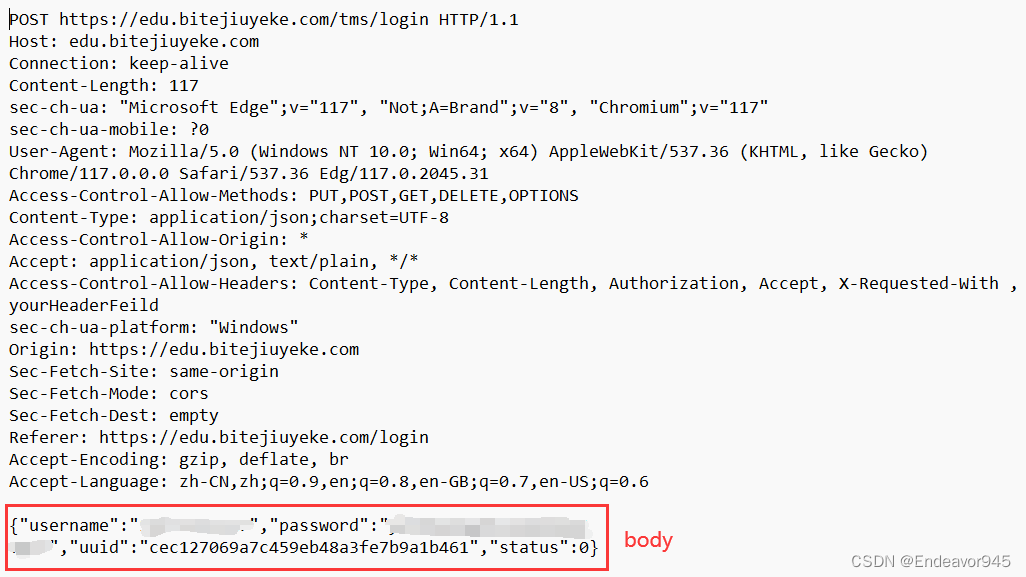
HTTP协议内容都是按照文本的方式明文传输的这导致在传输过程第三方者能够轻易获取传输的内容，而HTTPS在HTTP协议基础上引入一个加密以防止传输内容泄露或被篡改。
因此HTTPS是要比HTTPS更安全的，现在大部分网站采取的也都是HTTPS协议。

加密方式

加密就是把明文(要传输的信息)进行一系列变换,生成密文.
解密就是把密文再进行一系列转换,还原成对应的密文.
在加密和解密的过程中，一般需要一种或者多个中间转换的数据，来辅助这过程的正常进行，这种数据被叫做密钥.其作用就是为了防止他人获取其中的明文，造成隐患。

对称加密

最简单的保证安全的做法,就是引入对称密钥,针对传输的数据(HTTP的header和body)进行加密.
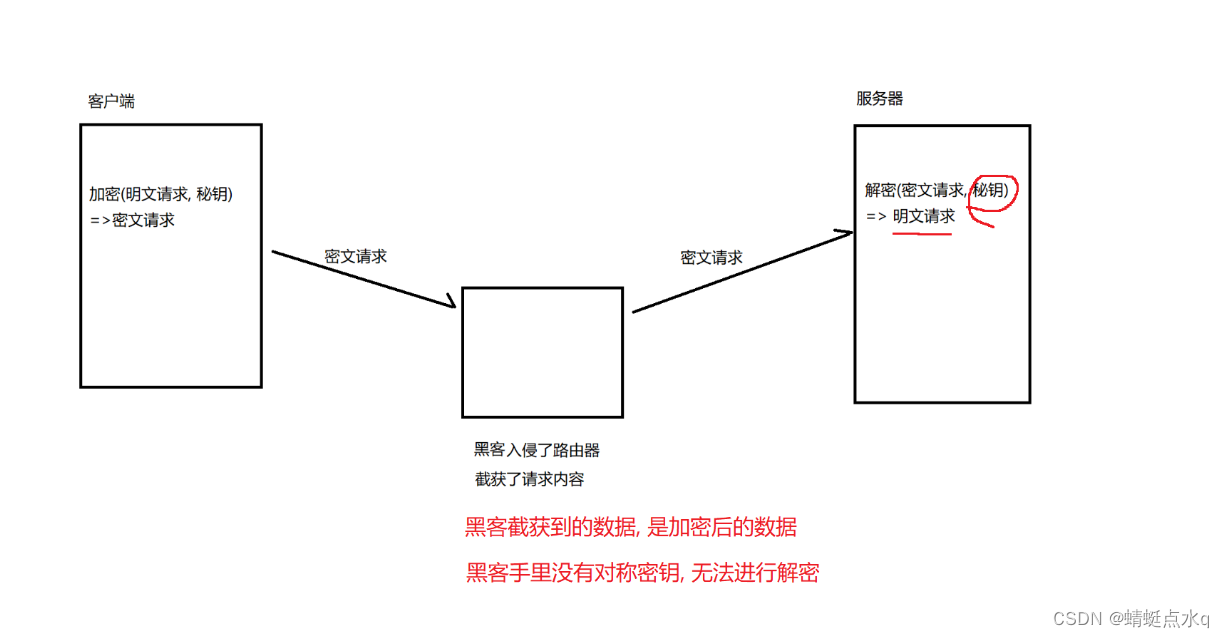
在这里插入图片描述
对称加密其实就是通过同一个 “密钥” ，把明文加密成密文，并且也能把密文解密成明文。
每个客户端,都需要有一把自己的对称密钥(不同客户端的密钥也要不同)如果客户端生成了密钥,就需要把密钥传输给服务器.

如果客户端直接将密钥进行明文传输给服务器，那么黑客也能获得密钥，那么后续的加密操作就没有任何用处了。因此，客户端在传输密钥的时候必须要给密钥进行加密。
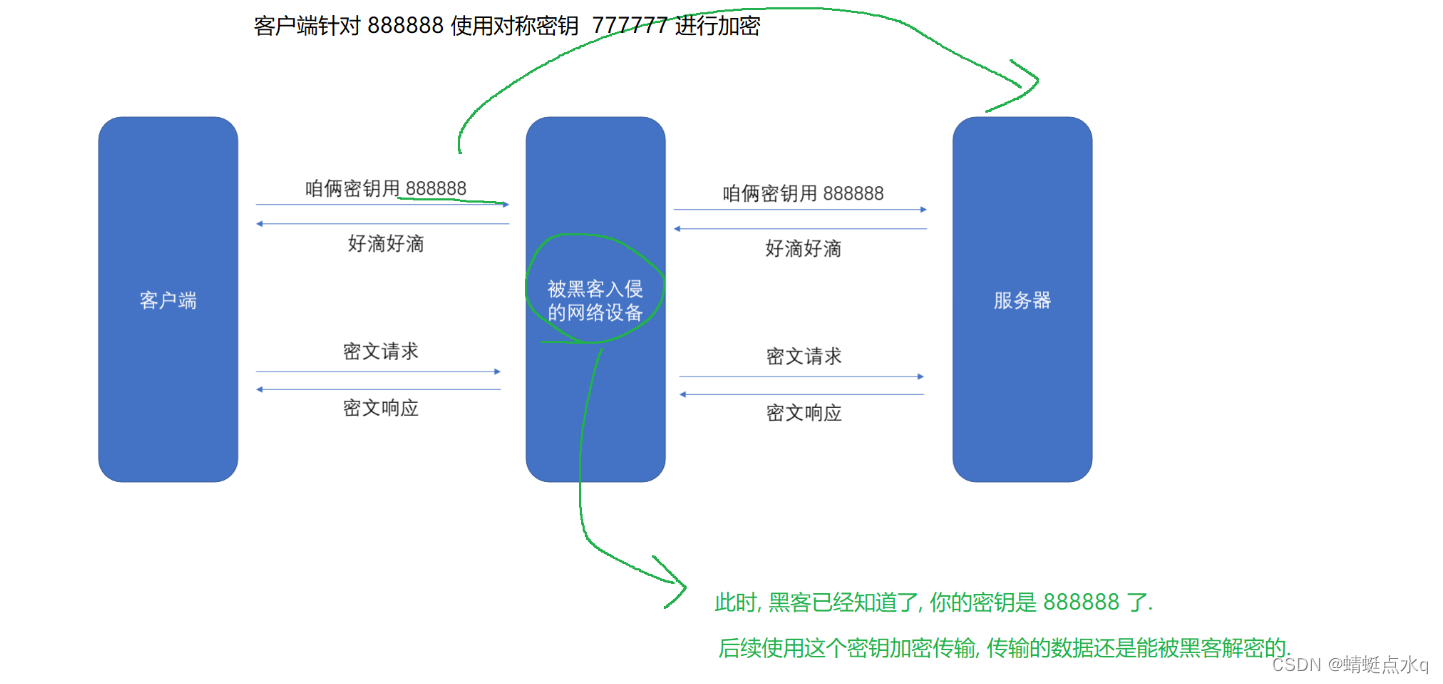
在这里插入图片描述
此时,就要想办法,把密钥安全地传输到对端,需要对这个对称密钥进行加密.
此时若使用对称加密,针对刚才对称密钥进行加密,就还是不行.不管搞几层,都是不安全的.
这时,就要使用非对称密钥进行加密了.

非对称加密

非对称加密要用到两个密钥，一个叫做公钥，另一个叫做私钥。私钥就可以对密文解密也可以对明文进行加密，公钥也一样。一般情况来说客户端可以获得公钥，而服务器一般使用私钥.

当客户端拥有公钥时，向服务器发送密钥时步骤如下：

客户端中先用公钥将密钥进行加密形成密文，再将密文发送给服务器
服务器接收到密文后，通过私钥对密文进行解密从而获取客户端给的密钥
再将收到密钥的信息发给客户端，让客户端知道自己已经收到密钥了
之后客户端就使用自己生成的密文进行对称加密来传递明文

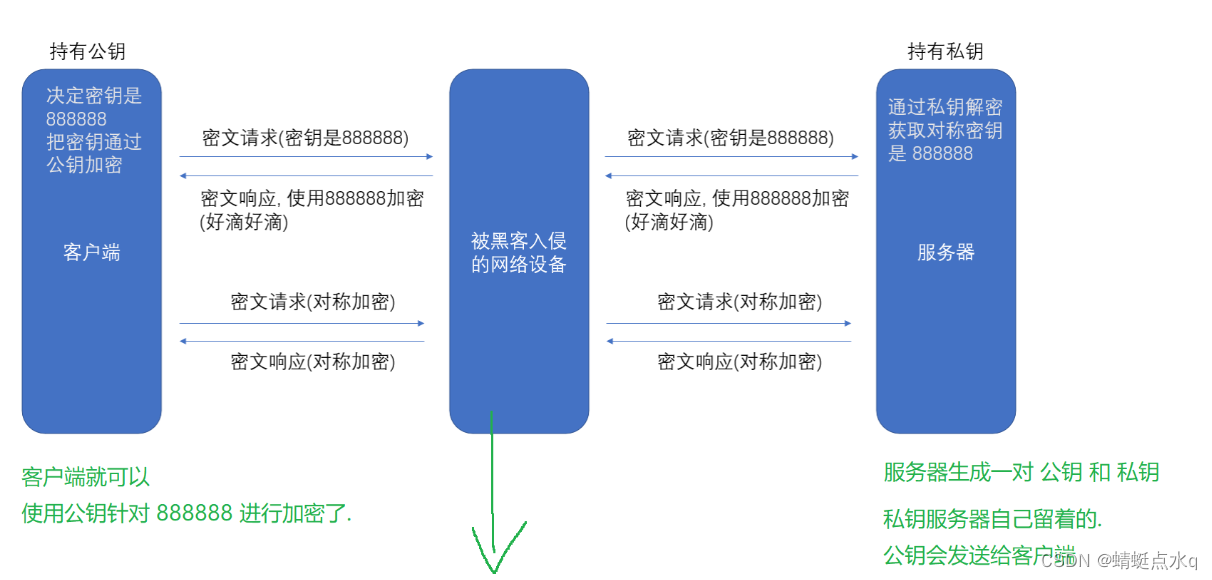
在这里插入图片描述
黑客能拿到 888888这样的密文，但是无法解密黑客手里也有公钥,但是没有私钥使用公钥加密，就必须使用私钥解密
只要能够把 888888 安全的传输过去此时后续的通信，就都可以使用对称加密，安全的进行了

注意
此处使用非对称加密,只是用来针对对称密钥进行加密而不会加密 http 的 header 和 body (数据),后续数据的加密还是使用对称加密的.
非对称加密,运算量很大,效率比较低.对称加密,运算量小,效率更高

引入证书

中间人攻击

上述的过程中,依然存在一个严重的问题,中间人攻击.
黑客可以使用中间人攻击的方式,仍然能够拿到对称密钥!
客户端是如何获取到服务器（某个网站）的公钥的？如何确保这个公钥不是被伪造的呢？
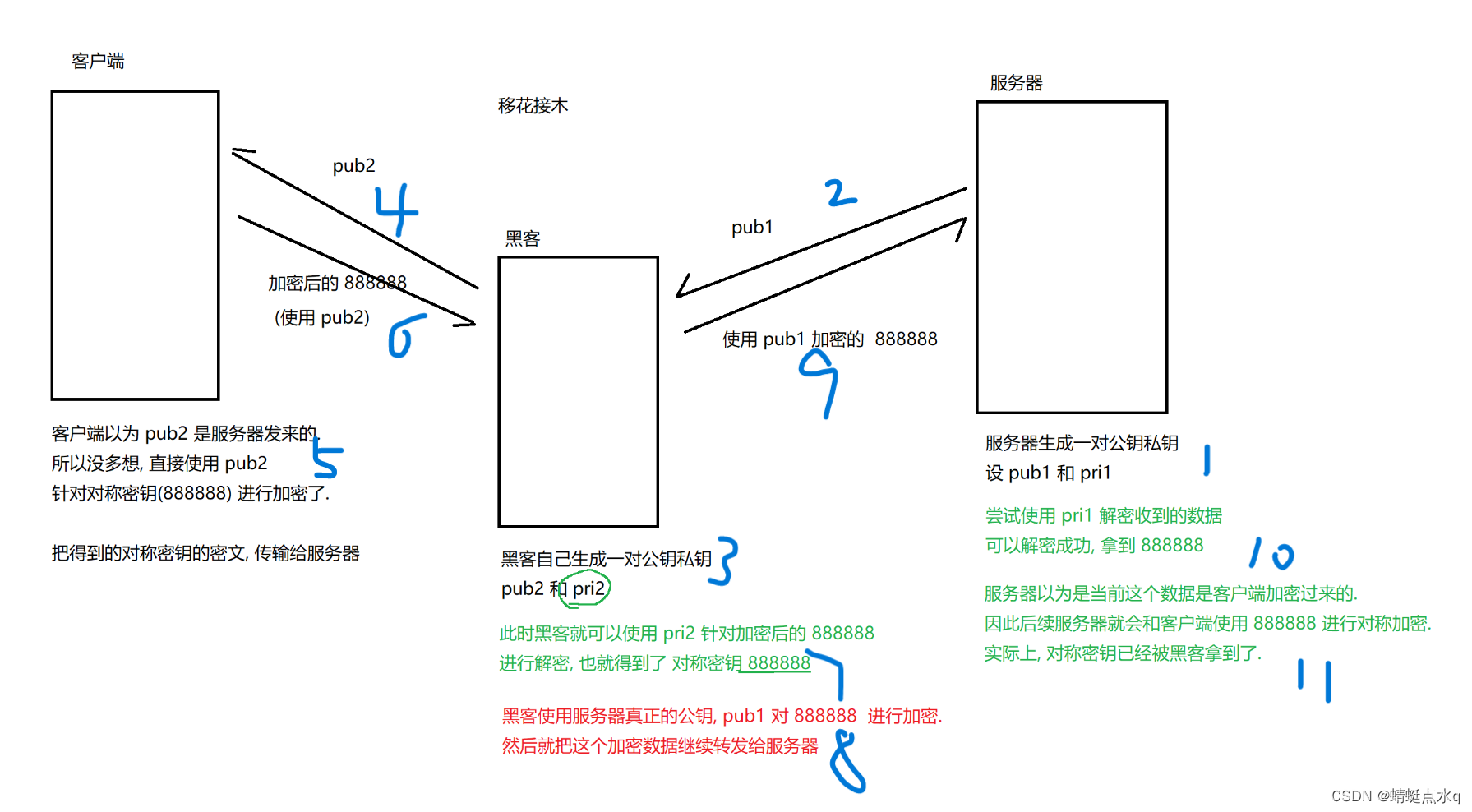在这里插入图片描述解决中间人攻击的关键，需要让客户端能够确认当前收到的公钥,确实是服务器返回的,而不是黑客伪造的!
这时候就引入了证书机制
需要有一个第三方的认证机构,通过第三方机构作保,来确认当前的公钥是有效的.
需要第三方机构对公钥进行认证.
这样客户端和服务器在连接的过程中，而不是简简单单地索取一个公钥了，而是直接向服务器索取一个证书，而相关的公钥就包含在证书里面。
这个证书不是服务器自己生成的，而是第三方机构颁发的，客户端拿到证书之后，就可以根据证书中的信息去第三方机构进行认证，来检验这个证书是否合法，从而确保公钥的可信性。