参考学习链接

计算机视觉与深度学习-04-图像去噪&卷积-北邮鲁鹏老师课程笔记

卷积的定义

在数学和信号处理中，卷积是一种数学运算，用于描述两个函数之间的关系。卷积可以看作是一种加权平均的操作，它将两个函数（通常是一个输入函数和一个响应函数）结合在一起，生成一个新的函数。

卷积运算通常用符号 “*” 表示。给定两个函数 f(x) 和 g(x)，它们的卷积定义为：

$$[(f\ast g)(x)={\int }_{-\infty }^{\infty }f(\tau )g(x-\tau )d\tau ]$$

或者在离散的情况下，对于离散函数 f[n] 和 g[n]，卷积定义为：
$$[(f\ast g)[n]=\sum _{m=-\infty }^{\infty }f[m]g[n-m]]$$
上述定义中，卷积运算将函数 g(x)（或 g[n]）沿着 x 轴（或 n 轴）进行翻转，并与函数 f(x)（或 f[n]）逐点相乘，然后对乘积进行积分（或求和）来获得新的函数 (f * g)(x)（或 (f * g)[n]）。

卷积后的图像

卷积的性质

叠加性

$$filer(f_1+f_2)=filter(f_1)+filter(f_2)$$
意味着两个信号（或函数）的卷积等于它们分别进行卷积后再相加。

平移不变性

$$filer(shift(f))=shift(filter(f))$$
卷积的平移不变性是指在进行卷积操作时，输入信号（或图像）的平移不会影响卷积操作的输出结果。换句话说，如果输入信号发生平移，那么卷积操作的输出也会相应地发生相同的平移。
即卷积以后平移和平移以后再卷积是一样的

交换律

$$a\ast b=b\ast a$$

结合律

$$a\ast (b\ast c)=(a\ast b)\ast c$$

分配律

$$a\ast (b+c)=(a\ast b)+(a\ast c)$$

标量

$$ka\ast b=a\ast kb=k(a\ast b)$$

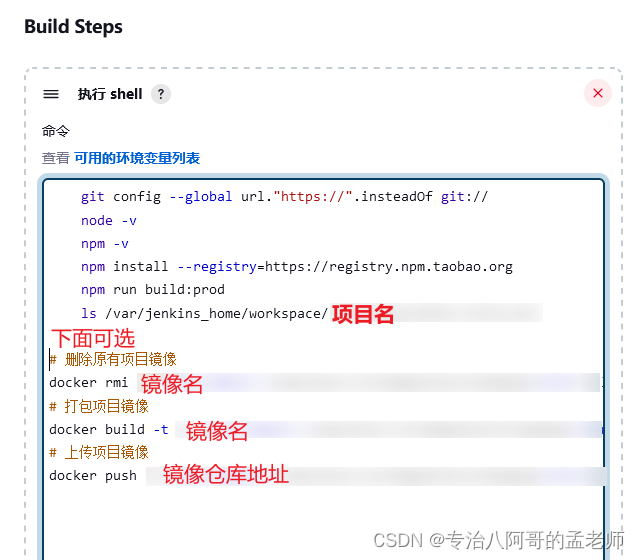
边界填充

为什么必须边界填充？

如果不进行边界填充，卷积结果的图像比原图像小一圈，卷积操作后的图像要小于输入时图像，通过边界填充，可以实现卷积前后图像的尺寸不变。

如果不进行边界填充，则卷积后的图像

边界填充方法 - 常数填充最常用

边界填充是在进行卷积操作时，在输入数据的边界周围添加额外的像素值。

常数填充

常数填充是指在边界上的像素周围添加一个固定的常数值。
常见的常数填充值包括零填充（常数为0）和边界值填充（常数为边界像素值）

具体而言，对于一个输入大小为 M × N 的图像，如果要在每个边界填充 p 个像素，常数填充会在输入图像的边界上添加 p 行和 p 列的像素，其中每个像素的值都是预先设定好的常数。

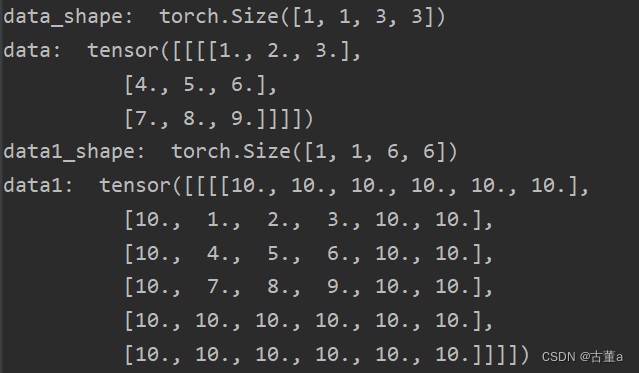
可以看到，分别在左边填充1列10元素，右边填充2列10元素，上边填充1列10元素，下边填充2列10元素。

零填充（zero padding）

零填充是指在边界上的像素周围添加值为零的像素。

具体而言，对于一个输入大小为 M × N 的图像，如果要在每个边界填充 p 个像素，则零填充会在输入图像的边界上添加 p 行和 p 列的零像素，使得填充后的图像大小变为 (M + 2p) × (N + 2p)

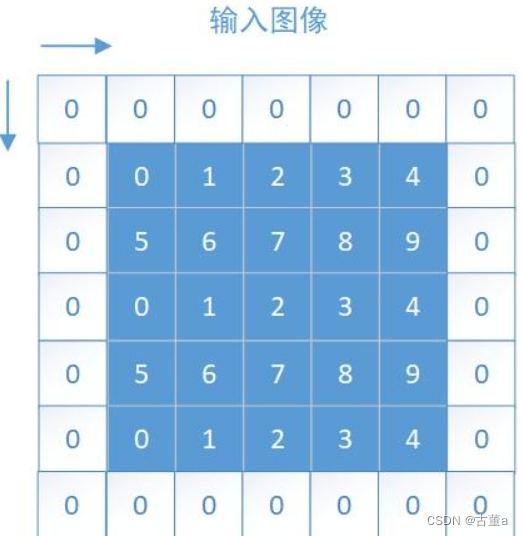
在零填充中，边界上添加的零像素值不包含任何信息，因此不会对卷积操作的结果产生影响。
零填充的主要目的是在进行卷积操作时，确保边缘像素有足够的邻域信息参与计算，从而避免边缘信息丢失。

拉伸

拉伸填充是指在边界上的像素值进行拉伸，使其扩展到填充区域。

具体而言，对于一个输入大小为 M × N 的图像，如果要在每个边界填充 p 个像素，则拉伸填充会将边界上的像素值复制或拉伸到填充区域，使得填充后的图像大小变为 (M + 2p) × (N + 2p)。

拉伸填充的目的是在进行卷积操作时，确保边缘像素有足够的邻域信息参与计算，避免边缘信息丢失。这对于保留输入数据的空间维度和边缘特征非常重要。
拉伸填充还可以防止卷积后输出特征图的尺寸缩小过快，使得网络能够在更多的空间位置上进行计算。

镜像

卷积示例

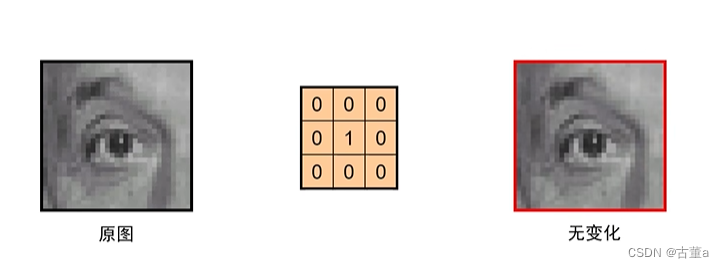
单位脉冲核

无变化

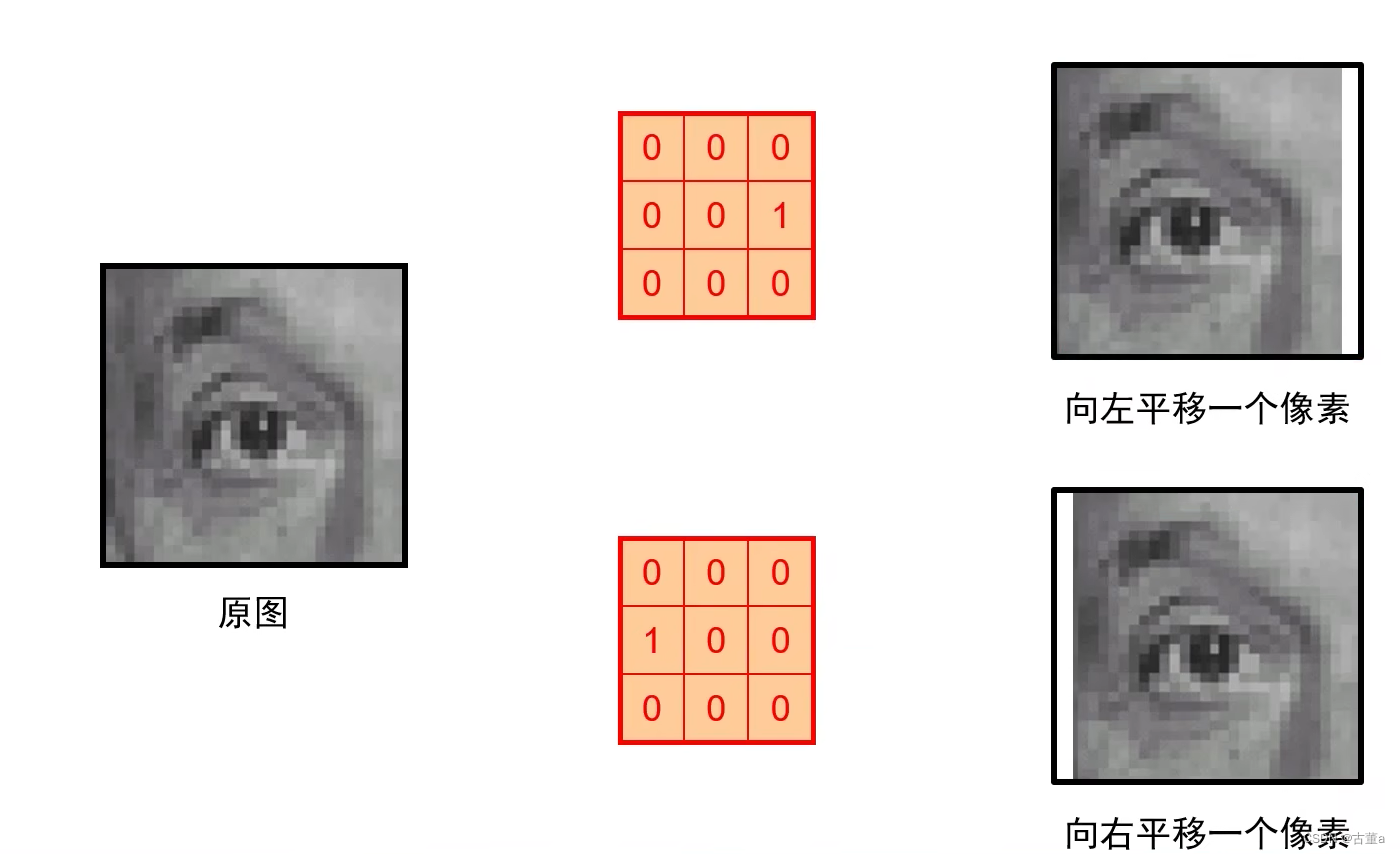
平移

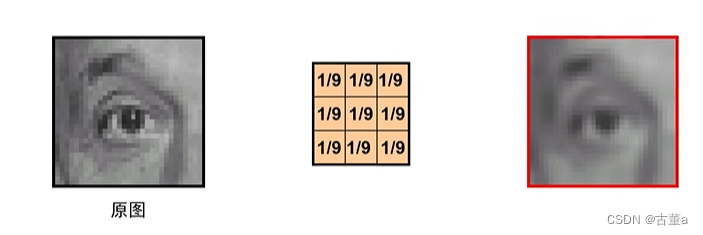
平滑

锐化

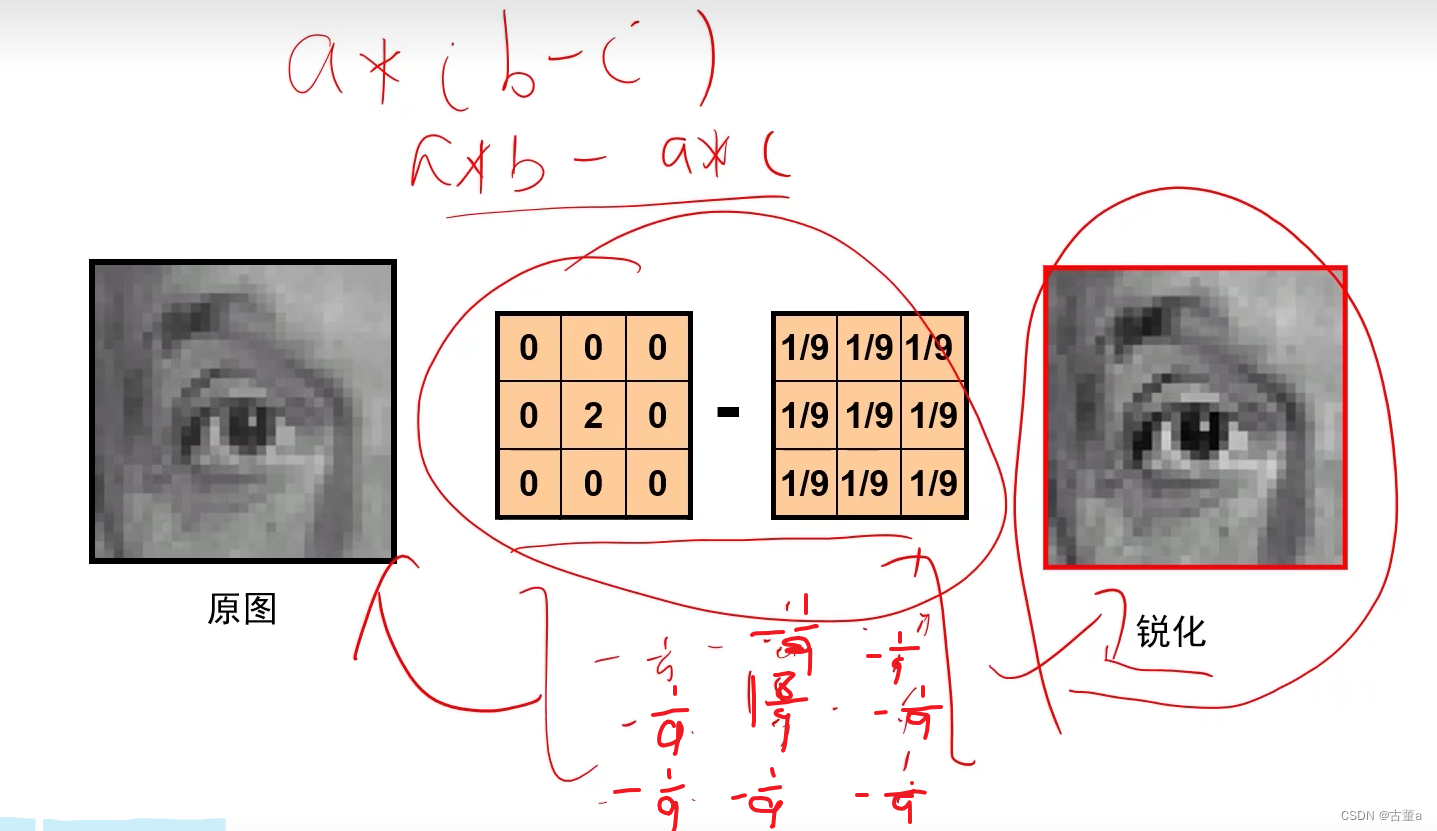
原图 - 平滑后的图 = 边缘图

在边缘处，原始图像中的像素值与平滑后的图像中的像素值之间存在较大的差异，因此在边缘图中会显示出明显的边缘。

原图 + 边缘图 = 锐化

将原式进行分解

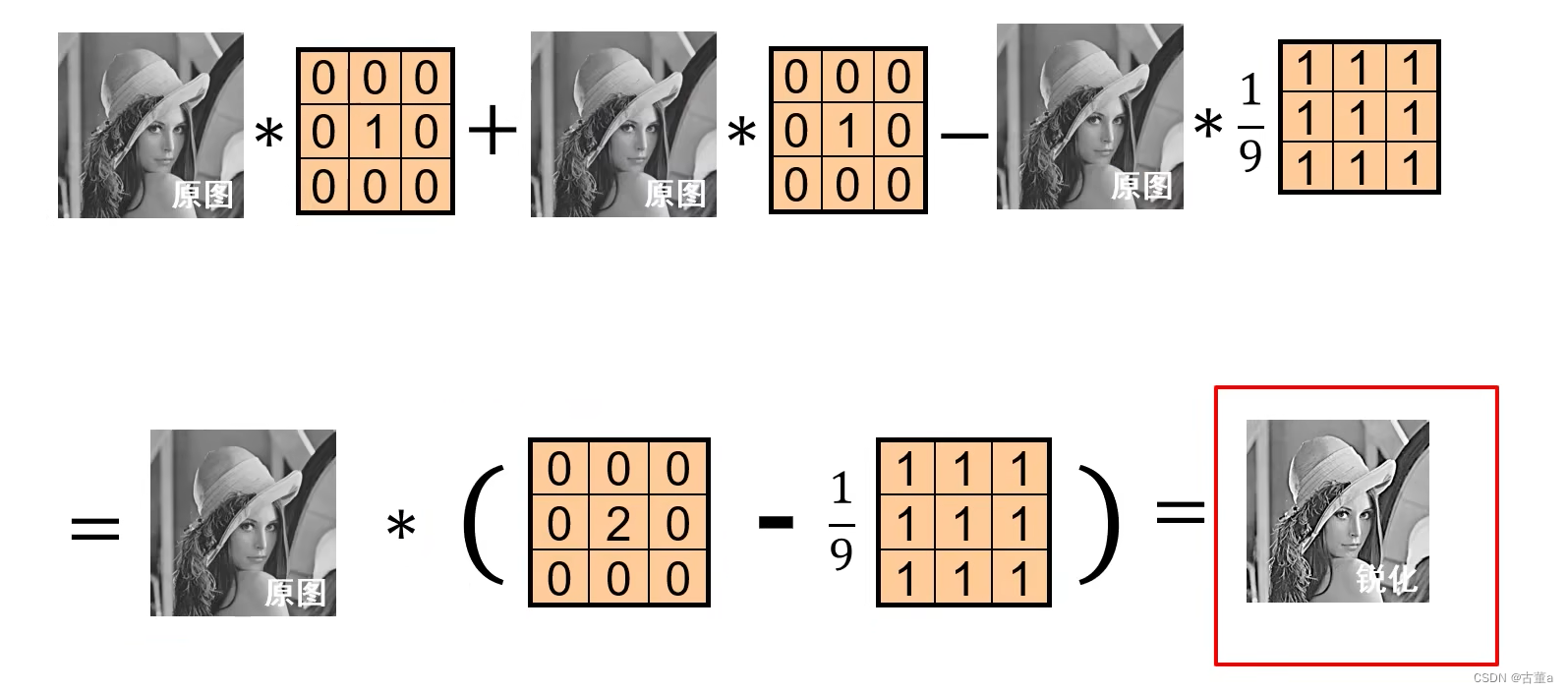
卷积核

平均卷积核

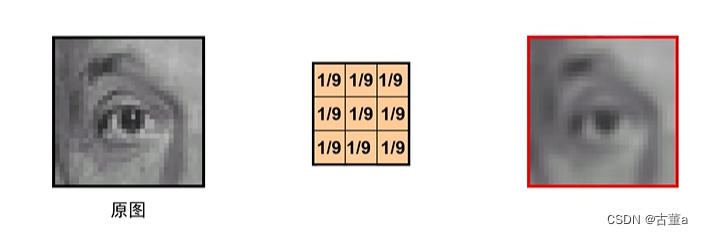
平均卷积核存在的问题

因为是与周围加权平均，所以卷积后的图像产生了一些水平和竖直方向的条状。 振铃！

其实对于平滑来说，卷积核中权重全都是1/9 ，显然这是不合理的。在这个过程中会损失图像的高频信息产生振铃效应。也就是卷积后的图像产生了一些水平和竖直方向的条状纹路。

图像处理中，对一幅图像进行滤波处理，若选用的滤波器具有陡峭（方的，不平滑）的变化，则会使滤波图像产生“振铃”，所谓“振铃”，就是指输出图像的灰度剧烈变化处产生的震荡，就好像钟被敲击后产生的空气震荡。

解决方法：根据邻域像素与中心的远近程度分配权重

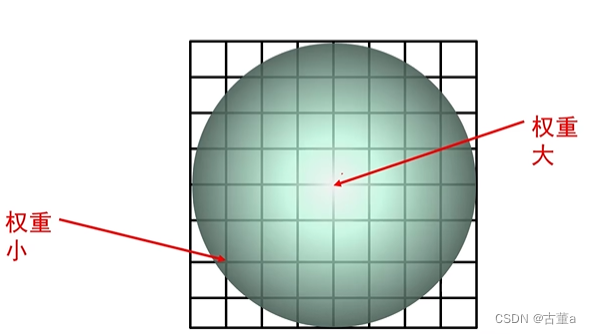
距离中心位置越远相应的权重就应该更小。这样的设置也更加合理一些。这就是 高斯核。

高斯卷积核

高斯卷积核定义

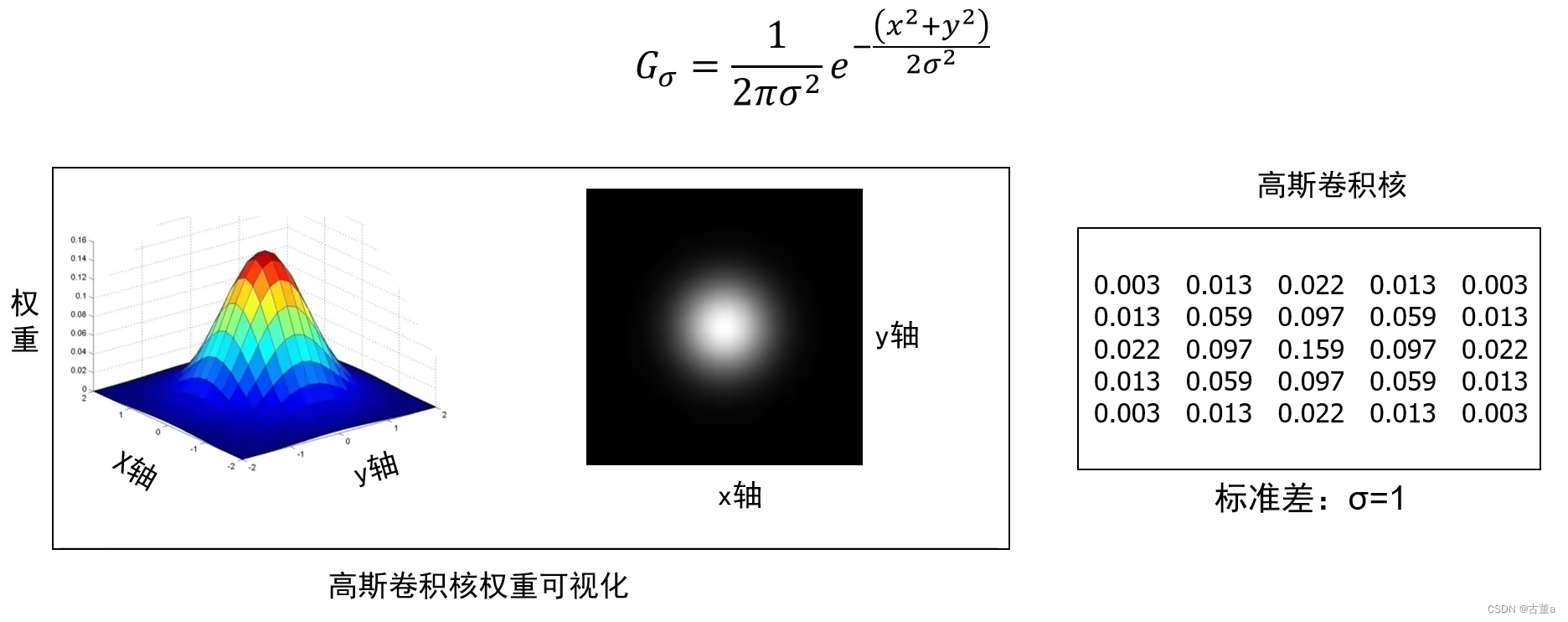
高斯卷积核生成步骤

1. 确定卷积核的尺寸
比如5x5

2. 设置高斯函数的标准差
比如σ=1

3. 计算卷积核各个位置权重值

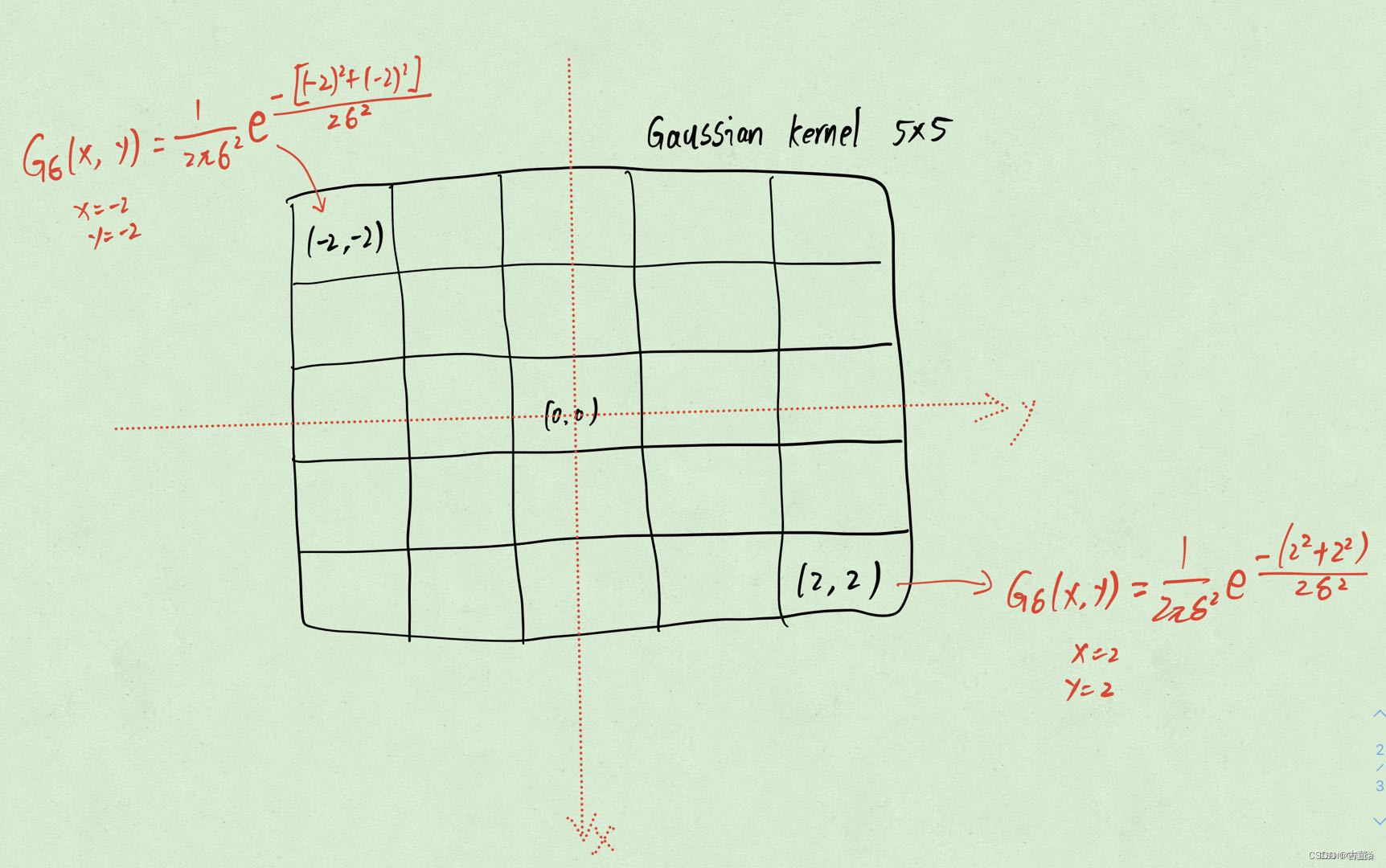
4. 对权重值进行归一化

需要注意的是在高斯核中，约束条件是所有权重相加和为1，这样做的目的是防止卷积后数据的衰减和溢出，因为无论RGB还是灰度图都在[0,255]内。

为什么要对权重值进行归一化？- 防止像素值的衰减和放大

• 如果所有权重的和小于1，假如是一张全白的图也即是像素值全为255，经过一个3×3 ，权重和不是1而是0.1的卷积核，得到输出结果却是25.5 ，显然这也不是想要的结果。

• 如果所有权重的和大于1，卷积后数据溢出（像素值被放大），改变了图像原始的0-255的范围。

只有所有权重的和等于1，卷积后的像素值范围不会改变。

因此，为解决该问题只需要将卷积核归一化即可，也就是卷积核中每一个值除以卷积核权重的总和，添加限制条件为权重和为1 。

高斯卷积核参数

高斯卷积核参数只有一个，高斯函数标准差σ。窗口尺寸可以由高斯函数标准差σ求出。窗口大小 = 23σ+1。

卷积核尺寸大小（窗口大小）

一般由高斯函数标准差σ求出。左边三倍的方差，右边三倍的方差，再加上自身

$$窗口大小=2\times 3\times \sigma +1。$$

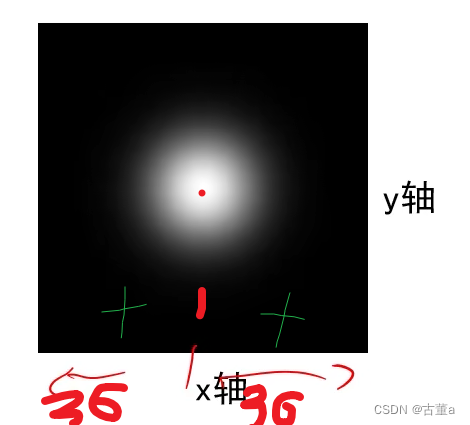
高斯函数标准差σ
其实就是标准差（方差），越大就会散布的越开，也即是窗宽相同，σ越大越扁，σ越小越突出，因为总面积要为1。

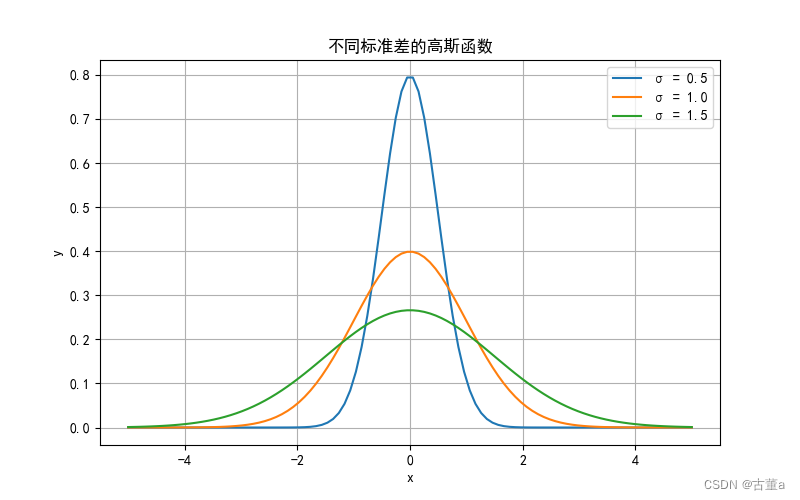
窗宽相同，总面积都为1，则

• 方差越大，中心权重越小，图像越平滑。
• 方差越小，中心权重越大，图像越陡峭。
  

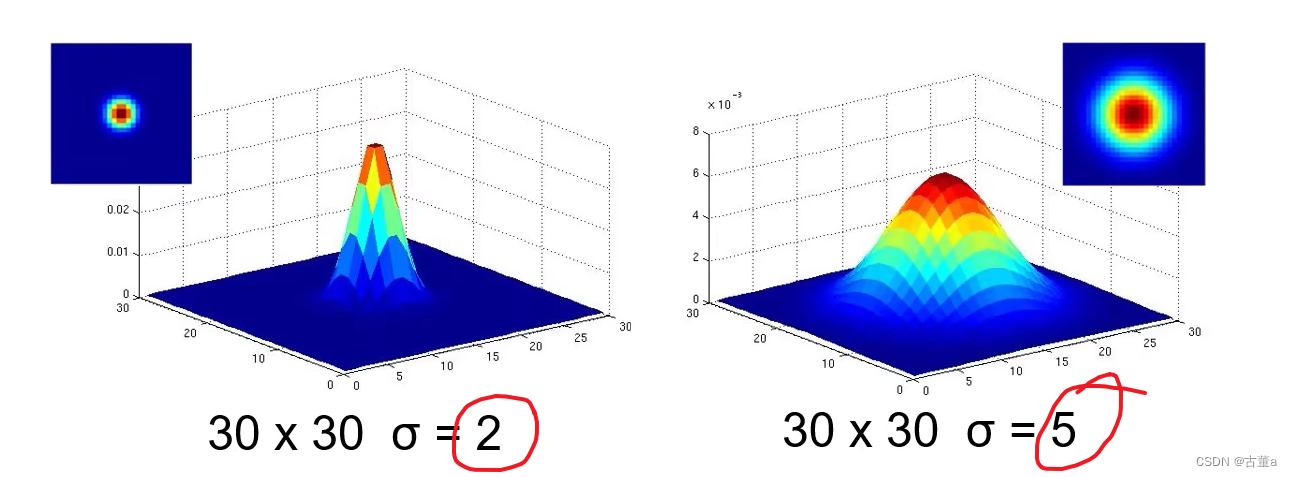
窗宽尺寸

同理，也可以通过固定方差σ去改变窗口大小。

当方差固定时，也就是说这个突出的最高中心点位置是相同的，而总面积又是相同的，归一化操作为（当前值/所有值之和），则

• 窗口越大，归一化中分子相同，分母越大，中心点权重占比越小，相对周围点权重占比越大，越平滑。
• 窗口越小，归一化中分子相同，分母越小，中心点权重占比越大，相对周围点权重占比越小，越陡峭。

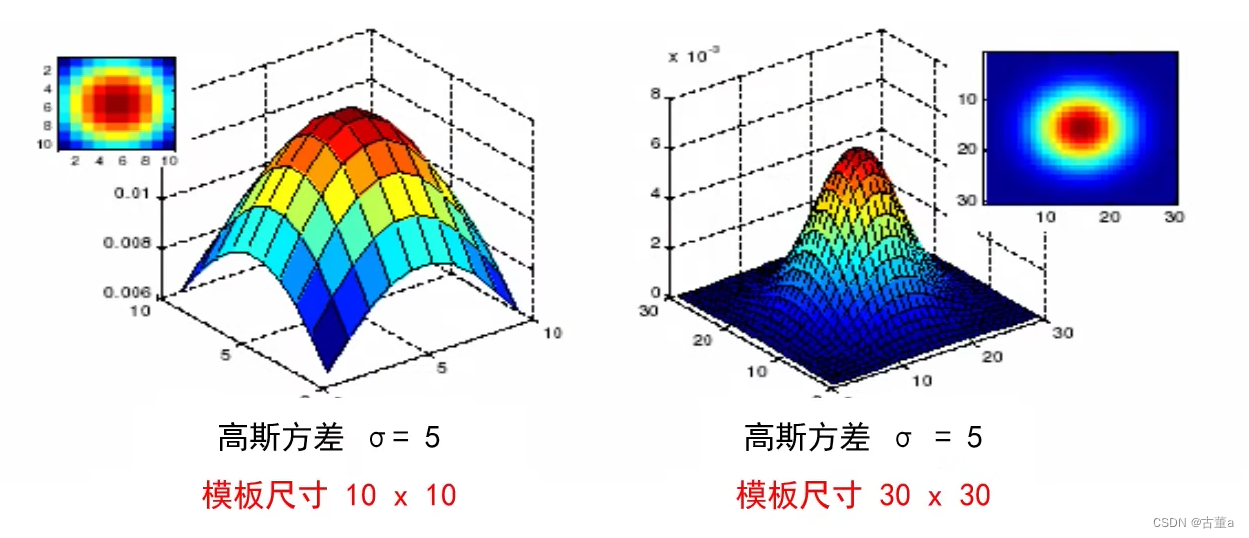
也就是说当方差固定时，窗口越小平滑的就越不明显，就会导致图像比较模糊。

这样一来，就会涉及到两个参数的选取问题，一般来说有个经验性的值。窗口大小为6σ+1。

高斯卷积核参数经验法则

为什么高斯卷积核窗口大小是23σ+1？

• 遵循3σ原则，基本可以包含99%以上的信号，甚至可以不用归一化。超过[-3σ,3σ]范围的信号很少。

• 高斯卷积核中心的左边和右边遵循3σ原则，所以是2x3σ，再加上自身1，所以是2x3xσ+1。

高斯核特性

1、去除图像中的“高频”成分（低通滤波器）

2、两个高斯卷积核卷积后得到的还是高斯卷积核

• 使用多次小方差卷积核连续卷积，可以得到与大方差卷积核相同的结果

• 使用标准差为 σ 的高斯核进行两次卷积与使用标准差 σ$\sqrt{2}$的高斯核进行一次卷积相同

高斯卷积对一副图像进行连续两次σ=1的高斯卷积输出结果等价于使用σ$\sqrt{2}$的高斯卷积一次的输出结果。这个满足勾股定理。

比如连续两次的高斯卷积核大小为2 σ ，3 σ 可以使用σ$\sqrt{2^2+3^2}$ 的卷积核代替。

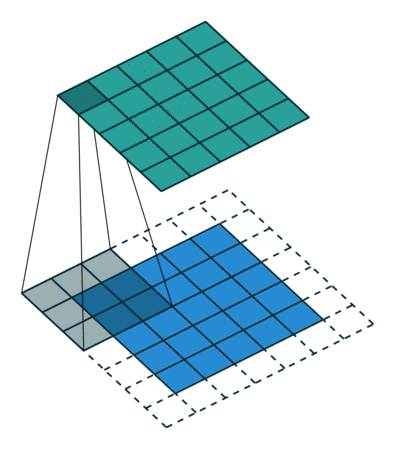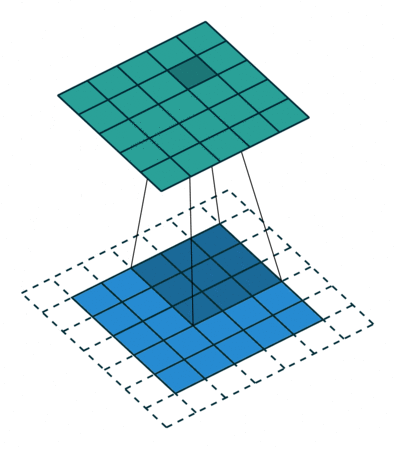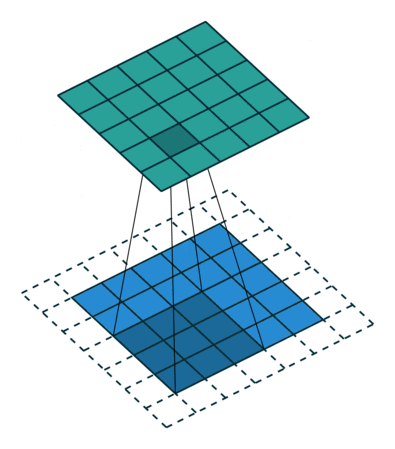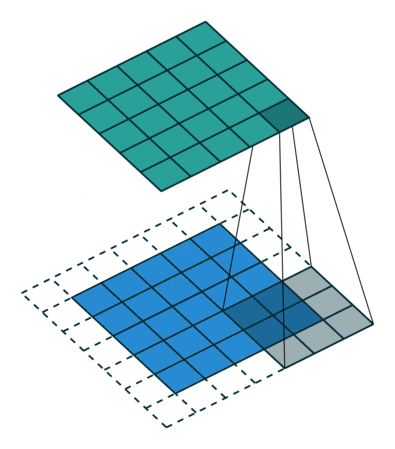
3、可分离

可分解为两个一维高斯的乘积

举个例子解释高斯核分解，假设有一个高斯卷积核与一个3x3大小的图像卷积（不考虑边界填充）得到应该是一个点。那么此时将高斯核拆解为两个一维向量，分别与图像进行卷积操作。它的主要作用就是加速。

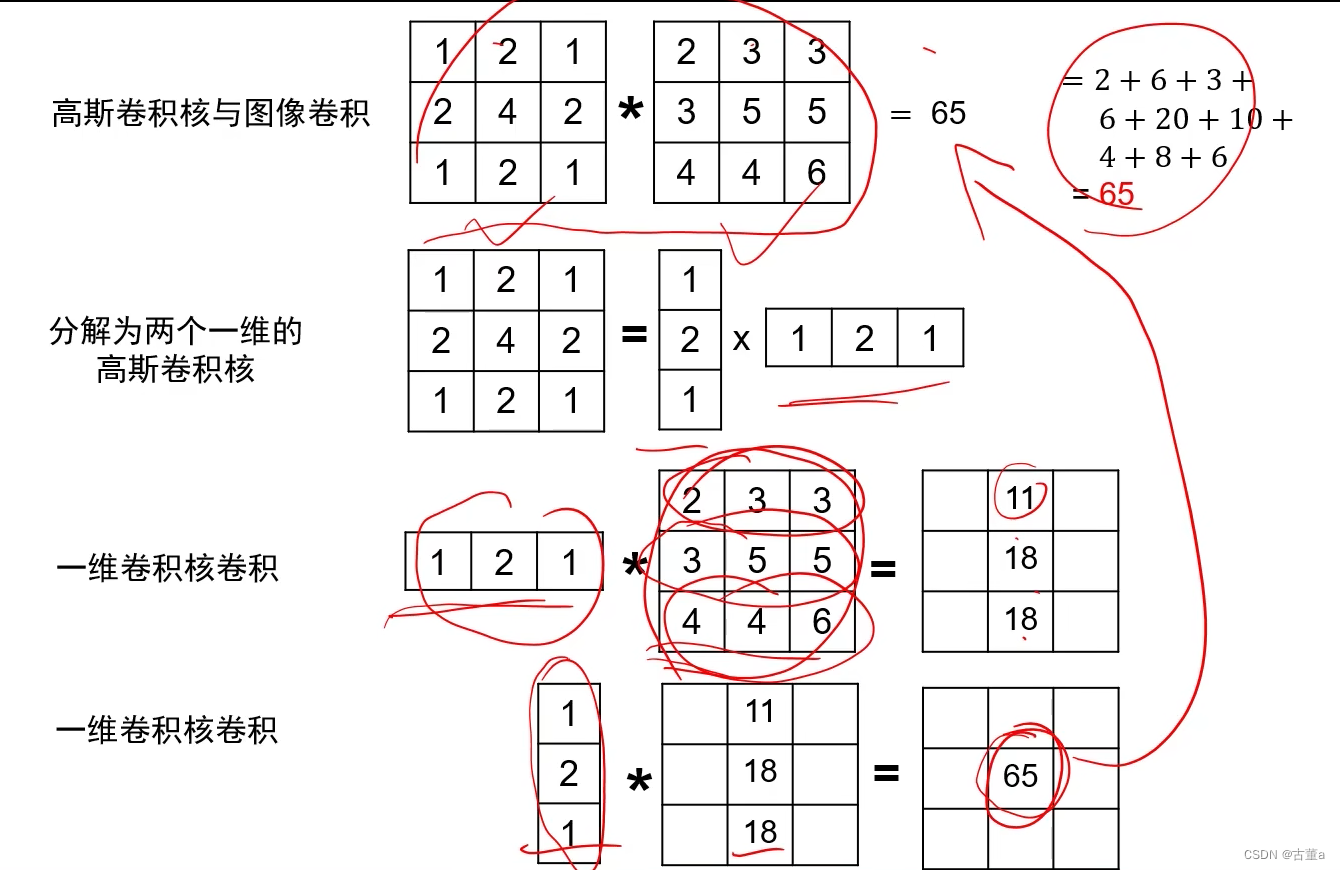
上图中的一维卷积核卷积不是向量乘矩阵，是进行卷积操作。

卷积核分解的作用（降低算法复杂度）

如果使用一个 m x m的卷积核对一幅n x n大小的图像进行卷积，考虑边界填充，算法复杂度为$O(n^2{m}^2)$

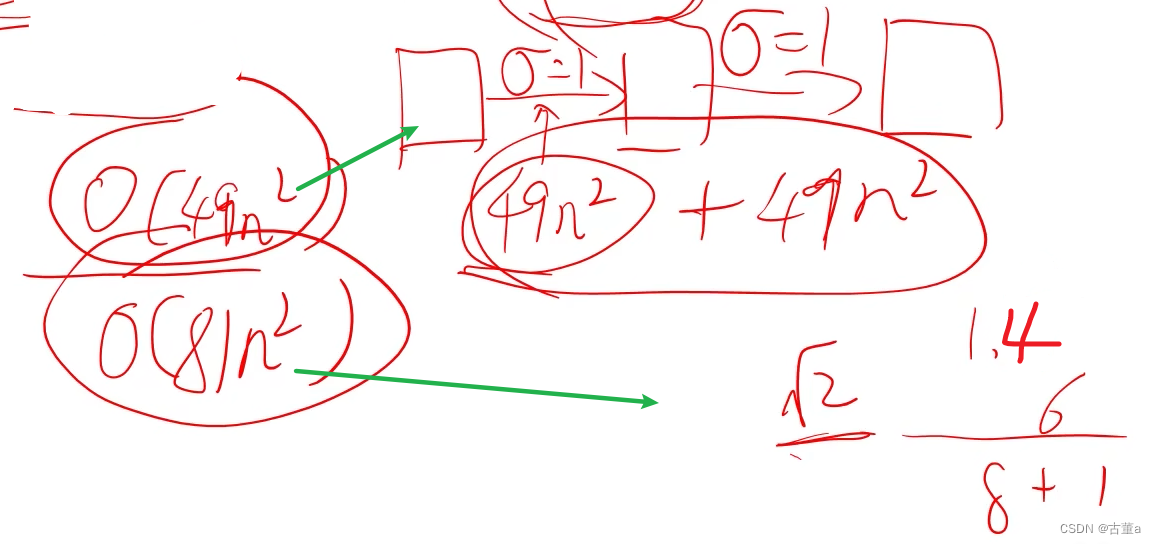
使用分解卷积算法复杂度$O(n^{2}m)$【其实这是x或者y一个方向上的复杂度】，也就是说如果对核进行分离，那么复杂度就能够降低一个等级，这是一件很有意义的事情。

从这里也可以看出来如果使用小核进行卷积也能够加速运算。

高斯卷积核vs平均卷积核