一、实验介绍

使用NumPy实现线性模型：梯度下降法

二、实验环境

本系列实验使用了PyTorch深度学习框架，相关操作如下：

1. 配置虚拟环境

conda create -n DL python=3.7

conda activate DL

pip install torch==1.8.1+cu102 torchvision==0.9.1+cu102 torchaudio==0.8.1 -f https://download.pytorch.org/whl/torch_stable.html

conda install matplotlib

 conda install scikit-learn

2. 库版本介绍

软件包	本实验版本	目前最新版
matplotlib	3.5.3	3.8.0
numpy	1.21.6	1.26.0
python	3.7.16
scikit-learn	0.22.1	1.3.0
torch	1.8.1+cu102	2.0.1
torchaudio	0.8.1	2.0.2
torchvision	0.9.1+cu102	0.15.2

三、实验内容

ChatGPT：

线性模型梯度下降法是一种常用的优化算法，用于求解线性回归模型中的参数。它通过迭代的方式不断更新模型参数，使得模型在训练数据上的损失函数逐渐减小，从而达到优化模型的目的。

梯度下降法的基本思想是沿着损失函数梯度的反方向更新模型参数。在每次迭代中，根据当前的参数值计算损失函数的梯度，然后乘以一个学习率的因子，得到参数的更新量。学习率决定了参数更新的步长，过大的学习率可能导致错过最优解，而过小的学习率则会导致收敛速度过慢。

具体而言，对于线性回归模型，梯度下降法的步骤如下：

初始化模型参数，可以随机初始化或者使用一些启发式的方法。

循环迭代以下步骤，直到满足停止条件（如达到最大迭代次数或损失函数变化小于某个阈值）：

a. 根据当前的参数值计算模型的预测值。

b. 计算损失函数关于参数的梯度，即对每个参数求偏导数。

c. 根据梯度和学习率更新参数值。

d. 计算新的损失函数值，并检查是否满足停止条件。

返回优化后的模型参数。

本实验中，gradient_descent函数实现了梯度下降法的具体过程。它通过调用initialize_parameters函数初始化模型参数，然后在每次迭代中计算模型预测值、梯度以及更新参数值。

0. 导入库

import numpy as np

1. 初始化参数

在梯度下降算法中，需要初始化待优化的参数，即权重 w 和偏置 b。可以使用随机初始化的方式。

def initialize_parameters():
    w = np.random.randn(5)
    b = np.random.randn(5)
    return w, b

2. 线性模型 linear_model

def linear_model(x, w, b):
    output = np.dot(x, w) + b
    return output

3. 损失函数loss_function

该函数接受目标值y和模型预测值prediction，计算均方误差损失。

def loss_function(y, prediction):
    loss = (prediction - y) * (prediction - y)
    return loss

4. 梯度计算函数compute_gradients

为了使用梯度下降算法，需要计算损失函数关于参数 w 和 b 的梯度。可以使用数值计算的方法来近似计算梯度。

def compute_gradients(x, y, w, b):
    h = 1e-6  # 微小的数值，用于近似计算梯度
    grad_w = (loss_function(y, linear_model(x, w + h, b)) - loss_function(y, linear_model(x, w - h, b))) / (2 * h)
    grad_b = (loss_function(y, linear_model(x, w, b + h)) - loss_function(y, linear_model(x, w, b - h))) / (2 * h)
    return grad_w, grad_b

5. 梯度下降函数`gradient_descent`

根据梯度计算的结果更新参数 w 和 b，从而最小化损失函数。

def gradient_descent(x, y, learning_rate, num_iterations):
    w, b = initialize_parameters()
    for i in range(num_iterations):
        prediction = linear_model(x, w, b)
        grad_w, grad_b = compute_gradients(x, y, w, b)
        w -= learning_rate * grad_w
        b -= learning_rate * grad_b
        loss = loss_function(y, prediction)
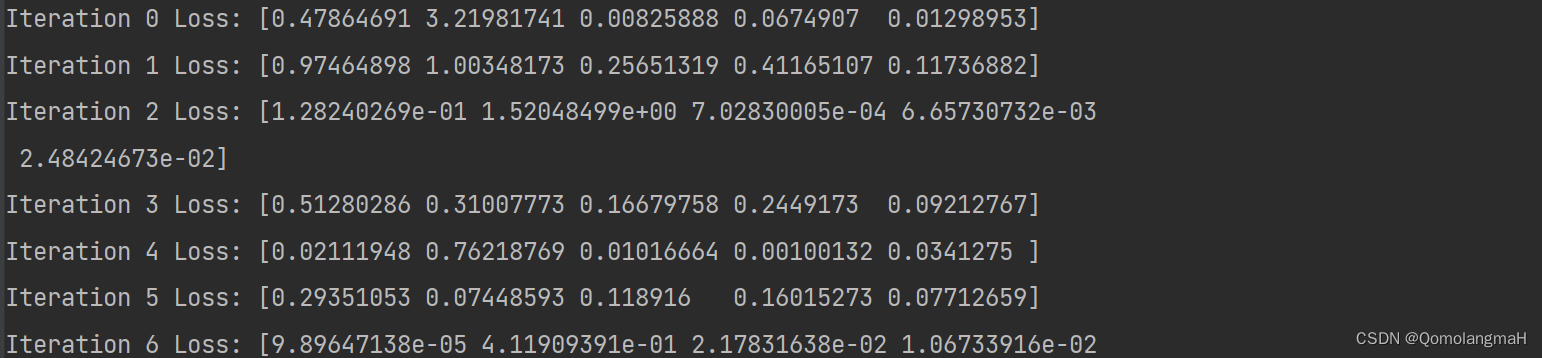
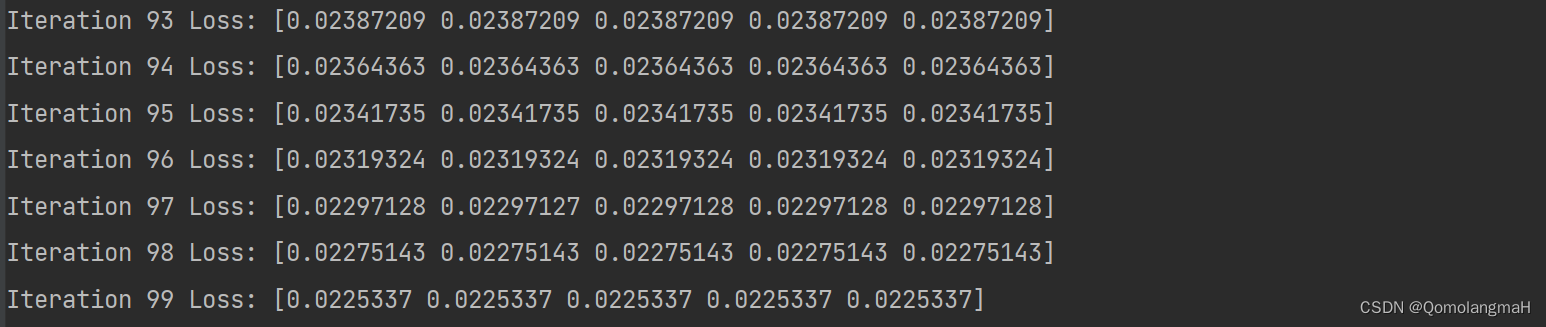
        print("Iteration", i, "Loss:", loss)
    return w, b

6. 调用函数

执行梯度下降优化：调用 gradient_descent 函数并传入数据 x 和 y，设置学习率和迭代次数进行优化。

x = np.random.rand(5)
y = np.array([1, -1, 1, -1, 1]).astype('float')
learning_rate = 0.1
num_iterations = 100
w_optimized, b_optimized = gradient_descent(x, y, learning_rate, num_iterations)

在上述代码中，每一次迭代都会打印出当前迭代次数和对应的损失值。通过不断更新参数 w 和 b，使得损失函数逐渐减小，达到最小化损失函数的目的。

希望这个详细解析能够帮助你优化代码并使用梯度下降算法最小化损失函数。如果还有其他问题，请随时提问！