问题描述

西西艾弗岛上散落着 n 块田地。每块田地可视为平面直角坐标系下的一块矩形区域，由左下角坐标 (x1,y1) 和右上角坐标 (x2,y2) 唯一确定，且满足 x1<x2、y1<y2。这 n 块田地中，任意两块的交集面积均为 0，仅边界处可能有所重叠。

最近，顿顿想要在南山脚下开垦出一块面积为 a×b 矩形田地，其左下角坐标为 (0,0)、右上角坐标为 (a,b)。试计算顿顿选定区域内已经存在的田地面积。

输入格式

从标准输入读入数据。

输入共 n+1 行。

输入的第一行包含空格分隔的三个正整数 n、a 和 b，分别表示西西艾弗岛上田地块数和顿顿选定区域的右上角坐标。

接下来 n 行，每行包含空格分隔的四个整数 x1、y1、x2 和 y2，表示一块田地的位置。

输出格式

输出到标准输出。

输出一个整数，表示顿顿选定区域内的田地面积。

样例输入

4 10 10
0 0 5 5
5 -2 15 3
8 8 15 15
-2 10 3 15

样例输出

44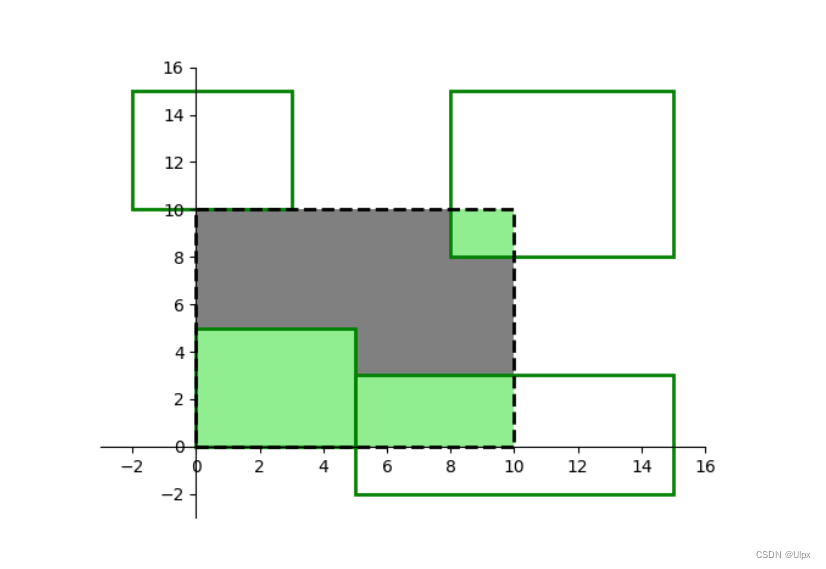

 

思路：

先按格式定义输入顶点位置就好，接着就是通过观察可以发现我们要求的矩形交叉面积就是对应两个大矩形左边界的较大值、右边界的较小值相减为一个边长，上边界的较小值、下边界的较大值相减为另一个边长，再将两边长相乘即可得到一个矩形的面积，依次将计算得到的矩形面积相加即可。

代码：

#include <iostream>
using namespace std;
int main()
{
    int n, a, b;
    int x1, y1, x2, y2;
    int x, y;
    int sum = 0;
    cin >> n >> a >> b;
    for(int i = 1; i <= n; i++){
        cin >> x1 >> y1 >> x2 >> y2;
        x = min(a, x2) - max(0, x1);
        y = min(b, y2) - max(0, y1);
        if(x >= 0 && y >= 0)
            sum += x * y;
    }
    cout << sum;
    return 0;
}