目录
一,单值二叉树
题目详情:
解法:父子比较法
解题思路:
思路实现:
源代码:
二,相同的树
题目详情:
解法:比较法
解题思路:
思路实现:
源代码:
三,翻转二叉树
解法:替换法
解题思路:
思路实现:
源代码:
一,单值二叉树
题目详情:
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树;
只有给定的树是单值二叉树时返回 true;否则返回 false;
提示:
1,给定树的结点树范围是【1,100】
2,每个结点的值都是整数,范围为【0,99】
示例1:
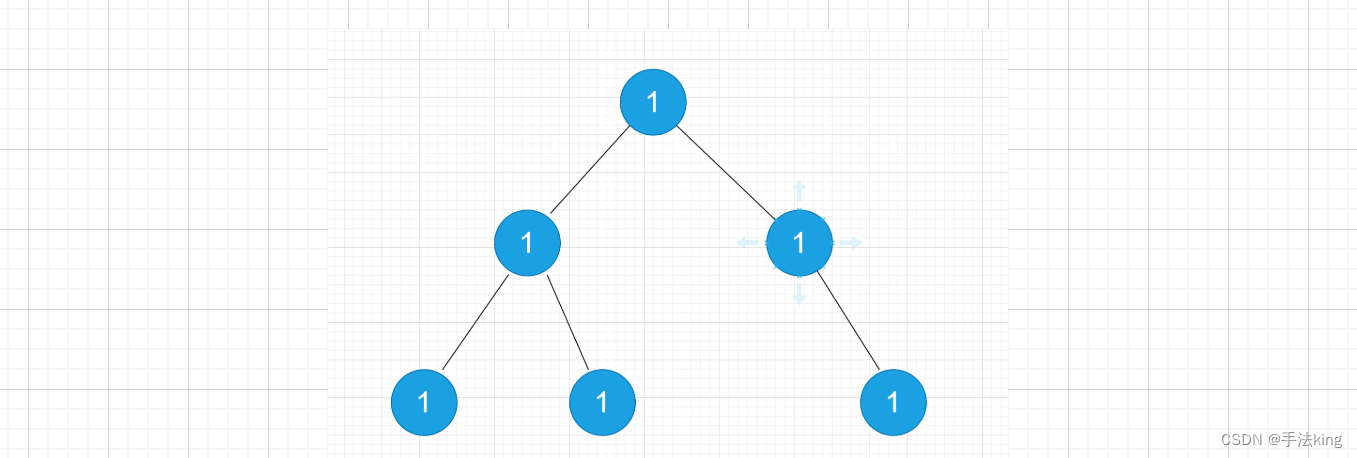
输入:nums = [1,1,1,1,1,NULL,1 ]
输出:true
示例2:
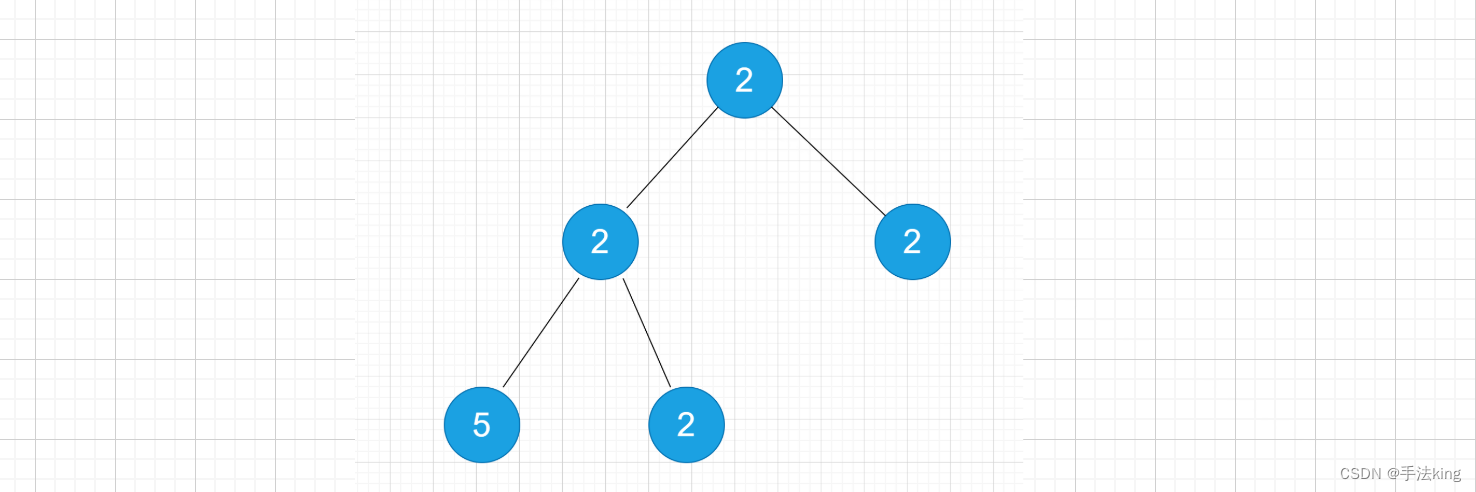
输入:nums = [2,2,2,5,2]
输出:false
解法:父子比较法
解题思路:
以上图为例:要判断根结点为(2)的二叉树是否为单值二叉树可以分解为(2)的左右子树是否为单值二叉树,这就很符合递归思路可以用递归解决;【(2)= 左子树 && 右子树】
判断条件:
当结点为NULL时返回 true ;
当子结点存在时,并且与父亲结点的值不相同时返回 false;
思路实现:
首先要判空:
//判断空
if(root==NULL)
{
return true;
}当结点为空时不影响父亲孩子之间的关系;
然后判断孩子,父亲之间的值的关系:
//判断孩子与父亲的值
if(root->left && root->val!=root->left->val)
{
return false;
}
if(root->right && root->val!=root->right->val)
{
return false;
}判断孩子,父亲所对应的值是否相同;
大事化小:以上条件都满足时,还需左右子树是否为单值二叉树,只有当左右子树都为单值二叉树时才为 true;
//化为两颗子树是否为单值树
return isUnivalTree(root->left) && isUnivalTree(root->right);要用逻辑与,需要双方为真时才返回 true;
源代码:
bool isUnivalTree(struct TreeNode* root){
//判断空
if(root==NULL)
{
return true;
}
//判断孩子与父亲的值
if(root->left && root->val!=root->left->val)
{
return false;
}
if(root->right && root->val!=root->right->val)
{
return false;
}
//化为两颗子树是否为单值树
return isUnivalTree(root->left) && isUnivalTree(root->right);
}我们可以用示例来演算一遍,流程也是这样的;
像这种递归题目要演算其过程需要画图,这样才是最直观的;
二,相同的树
题目详情:
给你两棵二叉树的根结点 p 和 q ,编写一个函数来检验这两棵树是否相同;
如果两个树在结构上相同,并且结点具有相同的值,则认为它们是相同的;
提示:
两棵树上的结点数目都在范围【0,100】内
-104<=Node.val<=10
示例1:
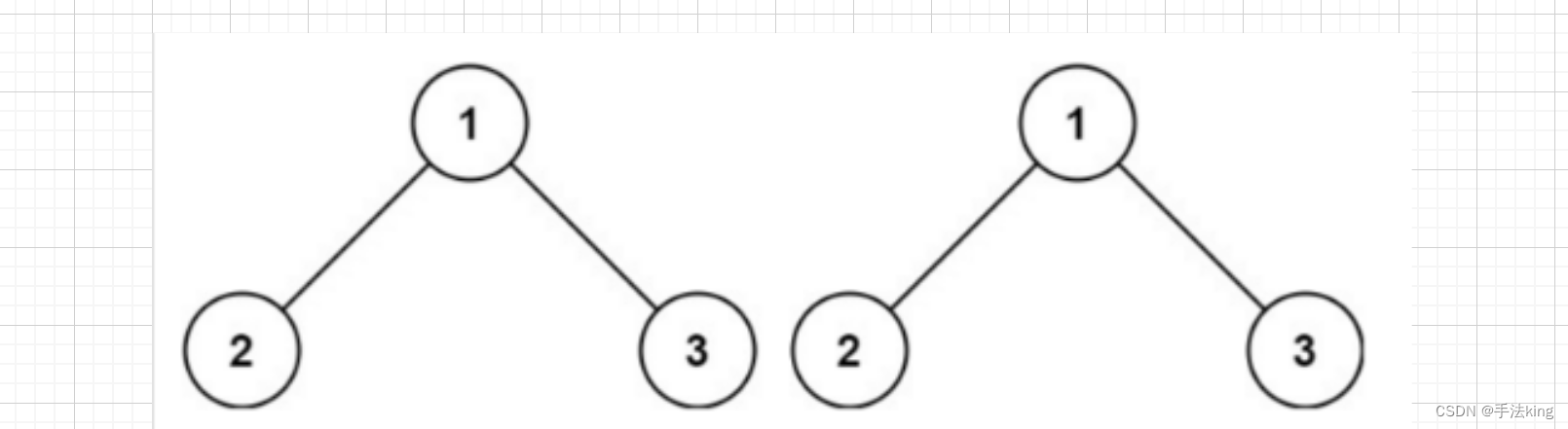
输入:p = [ 1,2,3 ],q = [ 1,2,3 ]
输出:true
示例2:

输入:p = [ 1,2 ],q = [ 1,2 ]
输出:false
示例3:
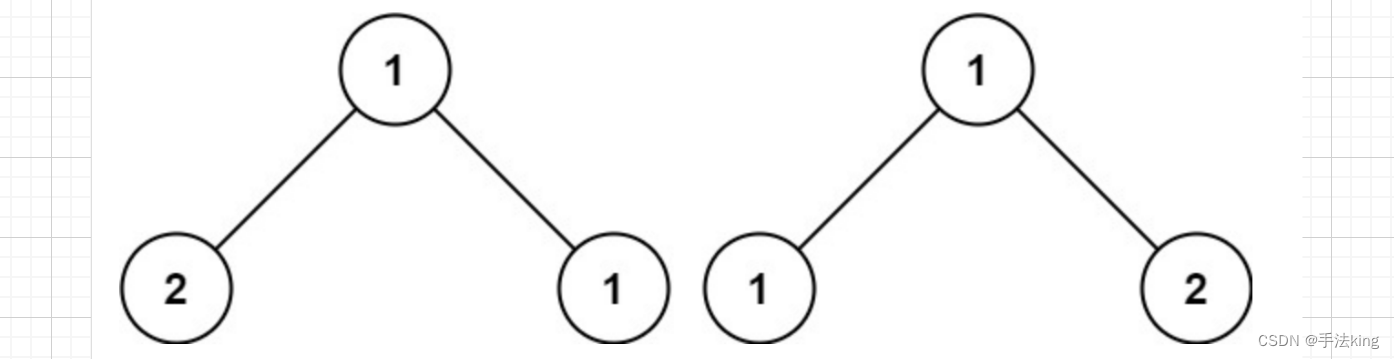
输入:p = [ 1,2,1 ],q = [ 1,2,2 ]
输出:false
解法:比较法
解题思路:
要判断两棵树是否一致,要考虑的是他们的结点是否都存在,结点对应的值是否相同;
以上图为例:根结点相同了,还要判断其左右子树是否也相同,然后层层往下,这道题也是用递归思想;
思路实现:
首先要判断他们的结点是否对应存在:
//双方都为空
if(p==NULL && q==NULL)
{
return true;
}
//一方为空另一方不为空
if((p==NULL || q==NULL)
{
return false;
}当双方对应的结点都为空时返回 true;
当双方对应的结点只有一方为空,另一方不为空时,返回 false;
然后判断它们对应的结点的值的情况:
//判断所对应的值是否相同
if(p->val != q->val)
{
return false;
}当所对应的值不相等则返回 false;
大事化小:当以上条件都满足时,还需要判断这两棵树所对应的左右子树是否相同;
//判断其对应的左右子树是否也相同
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);源代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//双方都为空
if(p==NULL && q==NULL)
{
return true;
}
//一方为空另一方不为空
if((p==NULL || q==NULL)
{
return false;
}
//判断所对应的值是否相同
if(p->val != q->val)
{
return false;
}
//判断其对应的左右子树是否也相同
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}这就是判断两颗二叉树是否相同问题的解题思路了,还是利用递归;
三,翻转二叉树
题目详情:
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点
示例1:
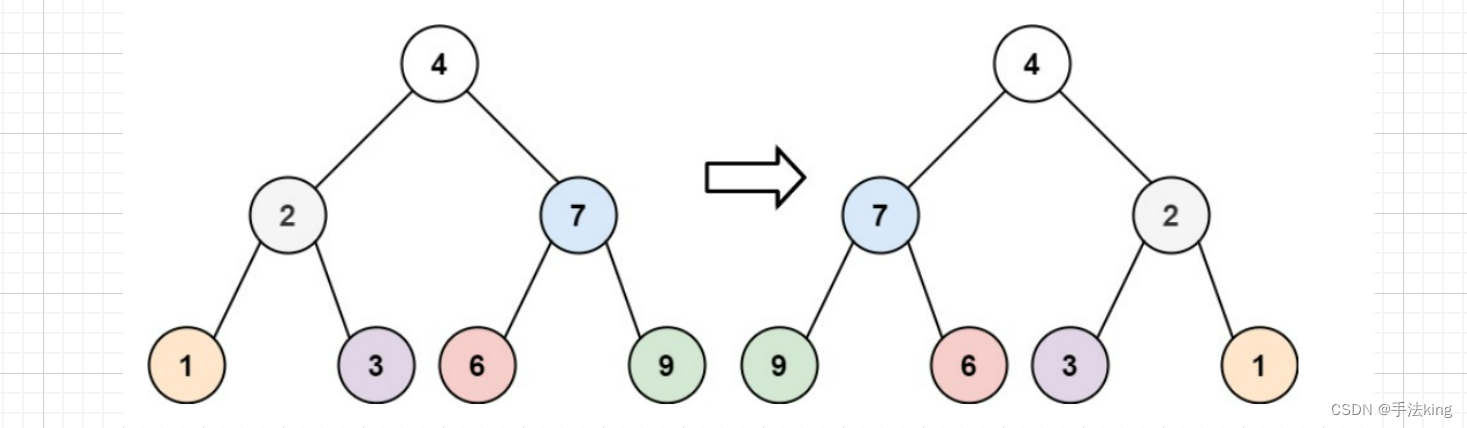
输入:root = [ 4,2,7,1,3,6,9 ]
输出:[ 4 7 2 9 6 3 1 ]
示例2:
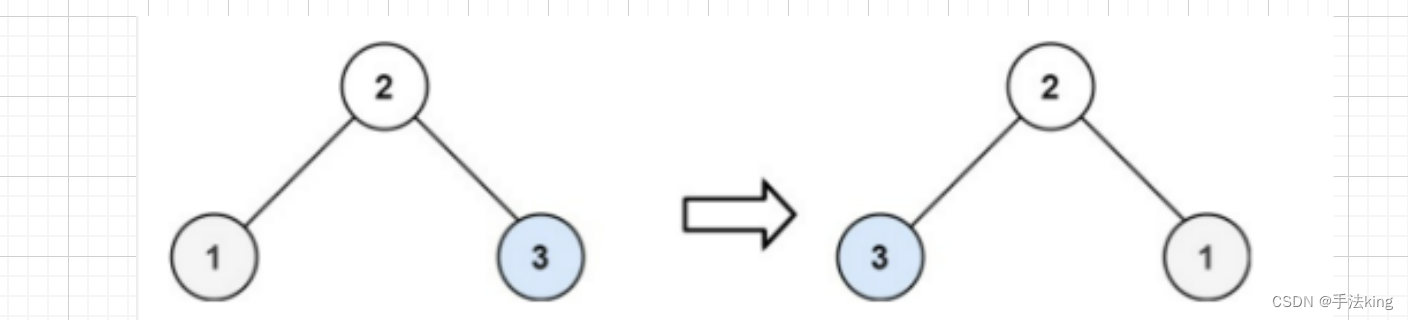
输入:root = [ 2,1,3 ]
输出:[ 2,3,1]
示例3:
输入:root = [ ]
输出:[ ]
解法:替换法
解题思路:
翻转翻转所谓翻转其实就是将左右子树换个位置而已,直接将其交换,层层交换下去直至NULL,用递归来实现;
思路实现:
首先还是判空,如果为空直接返回NULL即可;
然后直接交换左,右子树,再让其左,右子树也如此下去,就完成了对整颗树的翻转了,在返回根结点即可;
源代码:
void swap(struct TreeNode** left,struct TreeNode** right)
{
struct TreeNode* tmp=*left;
*left=*right;
*right=tmp;
}
struct TreeNode* invertTree(struct TreeNode* root){
//判空
if(root==NULL)
{
return NULL;
}
//交换
swap(&root->left,&root->right);
//左子树翻转
invertTree(root->left);
//右子树翻转
invertTree(root->right);
return root;
}基本上与二叉树相关的练习都要使用递归思想,前期培养递归思路最好就是画图解析,这个很重要,画图能让我们更直观的感受结点之间的关系,特别是感受那个返回的过程领悟其中的奥妙,久而久之我们对于递归的思路就更加清晰了,不至于摸不着北;
第五阶段就到这里了,这阶段带大家刷道些题目来感受一下二叉树的魅力!
后面博主会陆续更新;
如有不足之处欢迎来补充交流!
完结。。