机器学习——SVM（支持向量机）

news2024/9/24 5:27:51

0、前言：

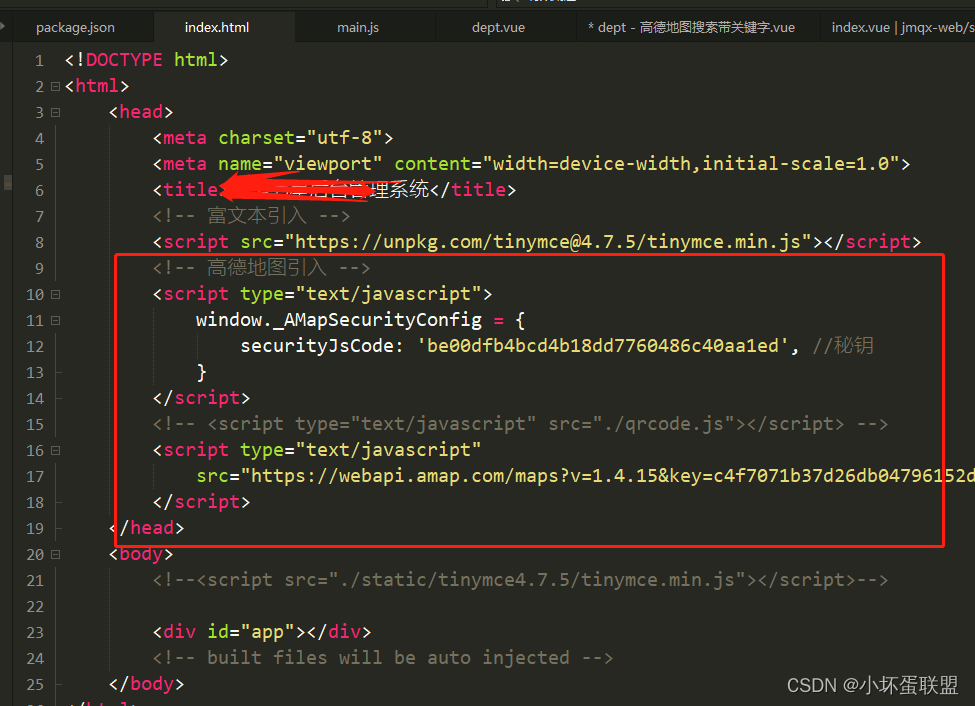
SVM应用：主要针对小样本数据进行学习、分类和回归（预测），能解决神经网络不能解决的过学习问题，有很好的泛化能力。（注意：SVM算法的数学原理涉及知识点比较多，所以应用比理解更重要）
原理：由二分类问题引出，如下图，问题是找到一条最宽的路劲划分两种分类，且路径1/2处的直线就是最优的直线。

进而将问题由二维（x轴和y轴）特征数据的分类拓展到更高维度的分类问题中，将问题转换为了多维问题，就会涉及向量和求极值，最终将支持向量的优化目标就由间隔最大化问题转化为了标准凸优化问题（标准凸优化是计算机当中数学问题的描述），然后就可以得到支持向量机算法。
支持向量机算法：
输入：m条训练数据S = {(x1,y1),(x2,y2),…,(xm,ym)}
前提：训练数据中正负采样存在分离平面
模型假设：H （关于w，x，b）
计算w和b的最优解
输出模型：H
支持向量机的对偶：将求解代约束的凸优化问题转化为求解它的对偶问题。然后借助拉格朗日求解对应的函数，这个函数的意义对于二维特征来说就是一条可以划分二分类问题的最优直线，对于三维特征来说就是一个可以划分空间中二分类问题的最优平面。
如下图所示就是二维特征的SVM所求直线A
如下图就是多维特征求最优划分的平面，因为在原始空间中，无法用一条直线划分，进而采用核技巧，将问题放到高维空间，进而划分数据，核技巧也称核变换是解决低纬度不可分问题的一个技巧。
支持向量机当中会有一些核函数，有线性核函数和高斯核函数。

1、支持向量机的分类示例：

目的：通过sklearn.datasets中的make_blobs生成2个类型的聚类，然后用SVC模型训练数据，借助模型的属性生成分类最优分界线，同时生成支持向量对应的直线
代码

# 导库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# SVM分类和回归库
from sklearn.svm import SVC,SVR
# 生成二分类数据
from sklearn.datasets import make_blobs
data,target = make_blobs(centers=2)
plt.scatter(data[:,0],data[:,1],c=target)
# 训练数据
# pd.DataFrame(data).head()
# data.shape,target.shape
sv = SVC(C=1,kernel='linear')
'''
SVC当中的参数说明：
1、C：越大表示约分类越严格，对于一些噪声就不%%sh略，可能会导致分类效果差
2、kernel：核函数，一般选默认的rbf，建议使用默认
'''
sv.fit(data,target)

# 画出通过SVM训练之后的最优分界线
# w1*x1+w2*x2+b=0
# 首先获取斜率和截距
# sv.coef_[0] # array([-0.69045562, -0.92961922])
# sv.coef_.shape # (1, 2)
w1,w2 = sv.coef_[0]
b = sv.intercept_[0]
# 画分界线
plt.scatter(data[:,0],data[:,1],c=target)
x1 = np.linspace(-7,-2,100)
x2 = -1 * (w1*x1+b)/w2
plt.plot(x1,x2,c='r')
# 画支持向量
x1_s = sv.support_vectors_[:,0]
x2_s = sv.support_vectors_[:,1]
plt.scatter(x1_s,x2_s,s=200,alpha=0.3,c='b')
# 画支持向量对应的直线，用虚线表示
b1 = -1*(w1*x1_s[1]+w2*x2_s[1])
b2 = -1*(w1*x1_s[2]+w2*x2_s[2])
x2_1 = -1 * (w1*x1+b1)/w2
x2_2 = -1 * (w1*x1+b2)/w2
plt.plot(x1,x2_1,linestyle='--',linewidth=5,c='r')
plt.plot(x1,x2_2,linestyle='--',linewidth=5,c='r')

结果

2、支持向量机回归示例：

目的：用SVM算法中的SVR预测sin函数
代码：

# 导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.svm import SVR
# 制作训练数据
x = np.random.random(150)*10
y = np.sin(x)

# 添加噪声
y[::5] += np.random.randn(30)*0.1

plt.scatter(x,y)
# 制作测试数据
x_test = np.linspace(0,10,100)
# 训练数据
sv_line = SVR(kernel='linear')
sv_line.fit(x.reshape(-1,1),y)
y_line_pred = sv_line.predict(x_test.reshape(-1,1))

sv_poly = SVR(kernel='poly')
sv_poly.fit(x.reshape(-1,1),y)
y_poly_pred = sv_poly.predict(x_test.reshape(-1,1))

sv_rbf = SVR(kernel='rbf')
sv_rbf.fit(x.reshape(-1,1),y)
y_rbf_pred = sv_rbf.predict(x_test.reshape(-1,1))
# 画图
plt.scatter(x,y)
plt.plot(x_test,y_line_pred,label='line',c='r')
plt.plot(x_test,y_poly_pred,label='ploy')
plt.plot(x_test,y_rbf_pred,label='rbf')
plt.legend(loc='lower left')