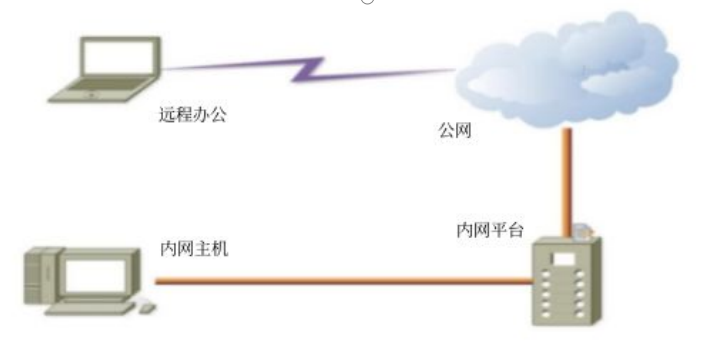
异地电脑远程桌面连接局域网服务器需求场景时，大多人会想到在目标本地的路由器上做端口映射设置。其实路由映射方法只适用于有公网IP的网络环境。当所在联网环境下是内部网络，内网环境下无公网IP或无公网IP权限时，路由映射方法就不生效了，有的场景甚至都没有路由权限。

面对内网环境，需要实现内外网互通互连远程访问，这里提供一种比较通用的方法：快解析端口映射。通过一步快解析软件添加内网映射域名设置，将内网IP端口让外网用域名地址格式来远程连接访问。下面以远程桌面连接为示例，其他SSH远程控制，或web网站，或其他项目应用场景同样可以参考，不同应用场景最大区别在于本地内网IP端口协议的不同。

1.内网桌面让外网远程连接的一步端口映射设置

在目标计算机本地或者所在内网另台互通内网的电脑上，安装并登录快解析软件并添加映射设置。通过这一步添加映射保存，将自己内网访问的地址转换成外网地址。
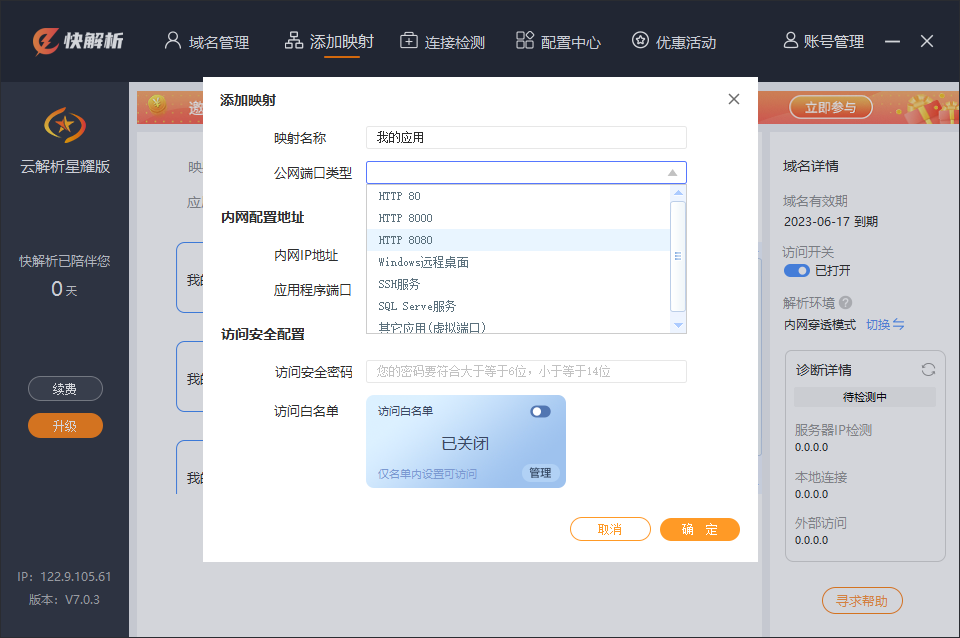
添加快解析映射时，根据自己应用场景选择合适的映射类型即可，如远程桌面连接一般推荐可以用非网站映射类型。
填写好对应内网地址和应用程序端口号，本机用127.0.0.1格式，非本机地址应用的用固定不变的内网地址格式。
添加映射点击确定生效后，不要退出快解析后台服务。如对内外网地址还是不明白或对选择填写有疑问的，可以将鼠标停留输入框等软件向导提示参考。

2.外网电脑通过域名进行远程控制指定的内部计算机

完成内网映射快解析添加保存设置后，当映射域名生效时，我们就可以在任意外网个人电脑远程到目标内网计算机像本地电脑一样操作了。在外网电脑发出远程访问时，使用快解析映射后的域名地址和外网端口号。

这样就完成跨网异地外网对内网计算机远程桌面的连接，我们可以用这种方法像操作自己的电脑一样来通过远程桌面进行文件、资料、系统应用等等的查询与操作，十分的方便与实用。

只有先确保内网可以正常远程桌面连接访问，映射外网后才能正常访问。同时确保添加映射填写使用的内外网地址的准确性。

外网远程控制连接访问内网计算机，就是这么简单。实质就是先在内网上，通过快解析一步添加映射设置，将内网远程地址变为外网域名地址。外网远程桌面连接内网windows，及外网远程SSH内网Linux主机都是同样可以设置使用，区别只是在于目标内网地址端口号，以自己本地实测填写设置映射外网即可。