文章目录
- 一.哈夫曼编码原理
- 哈夫曼二叉树构建
- 二.具体代码实现
一.哈夫曼编码原理
哈夫曼编码(Huffman Coding)是一种用于数据压缩的编码方法,它通过给出不同的数据符号分配不同长度的编码,使得出现频率高的符号具有较短的编码,而出现频率低的符号具有较长的编码,从而达到压缩数据的目的。
哈夫曼编码的原理可以通过以下步骤来解释:
统计频率:首先,需要统计待编码数据中每个符号的出现频率。符号可以是字符、字节或其他数据单元。统计频率可以通过遍历整个数据集来完成,并记录每个符号出现的次数。
构建编码树:根据符号的频率构建一个特殊的二叉树,称为哈夫曼树(Huffman Tree)或编码树。构建编码树的方法是将频率最低的两个符号合并为一个新节点,该节点的频率为两个节点频率之和。将新节点插入到已有节点的集合中,重复这个步骤,直到只剩下一个节点,即根节点为止。在构建过程中,可以使用优先队列或最小堆来维护频率最低的节点。
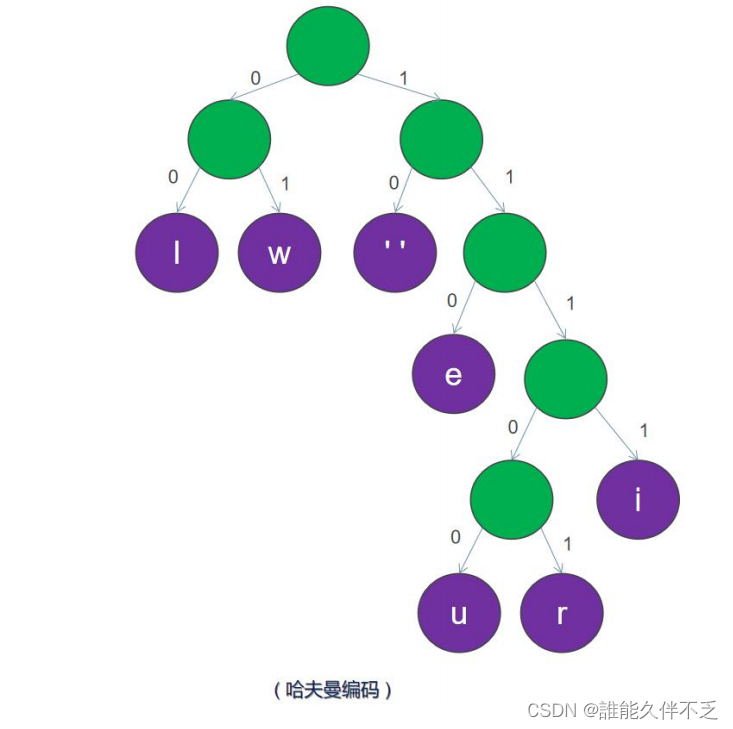
分配编码:从根节点开始,沿着左子树走为0,沿着右子树走为1,将0和1分别分配给左右子节点。重复这个过程,直到遍历到每个叶子节点为止。每个叶子节点的路径上的0和1的序列就是对应符号的哈夫曼编码。
生成编码表:将每个符号及其对应的哈夫曼编码存储在一个编码表中,以备后续的编码和解码使用。
进行编码:将原始数据中的每个符号替换为其对应的哈夫曼编码,生成压缩后的编码数据。由于频率高的符号具有较短的编码,而频率低的符号具有较长的编码,所以整个编码后的数据长度会相对减小。
哈夫曼编码的优点是没有冗余和歧义性,即每个编码都不是其他编码的前缀,这种性质被称为前缀码。这使得编码和解码过程都是非常高效的。然而,对于哈夫曼编码的最佳性能,符号的频率应该是根据数据集的统计特征进行调整的。
哈夫曼编码举例: 假设要对“we will we will r u”进行压缩
压缩前,使用 ASCII 码保存
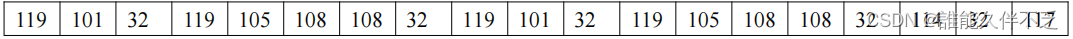
共需: 19 个字节 - 152 个位保存
下面我们先来统计这句话中每个字符出现的频率。如下表,按频率高低已排序:

接下来,我们按照字符出现的频率,制定如下的编码表:

这样,“we will we will r u”就可以按如下的位来保存:
01 110 10 01 1111 00 00 10 01 110 10 01 1111 00 00 10 11101 10 11100
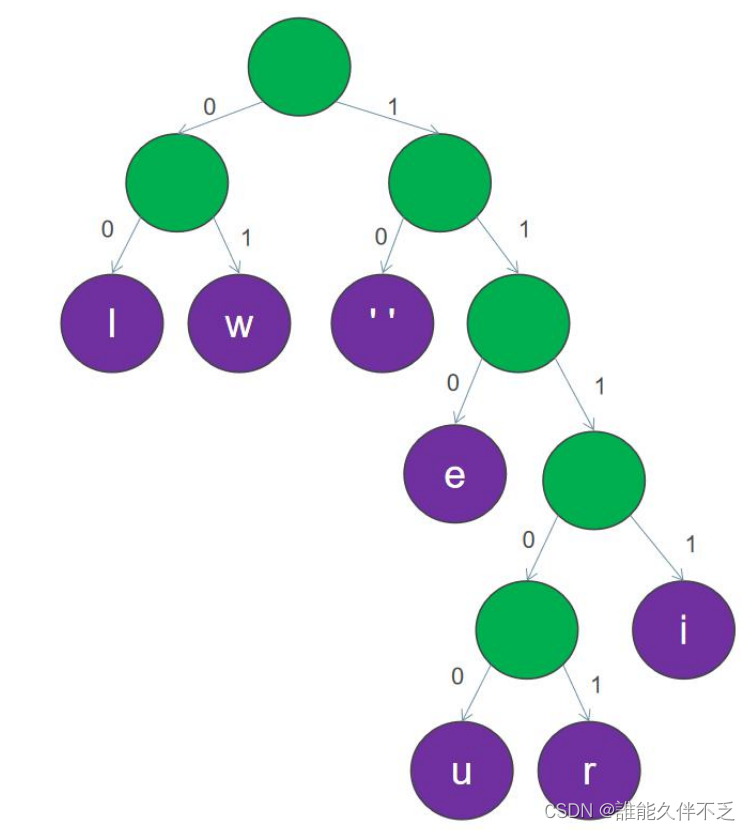
哈夫曼二叉树构建
1.按出现频率高低将其放入一个数组中,从左到右依次为频率逐渐增加


2. 从左到右进行合并,依次构建二叉树。第一步取前两个字符 u 和 r 来构造初始二叉树,第一个字符作为左节点,第二个元素作为右节点,然后两个元素相加作为新的空元素,并且两者权重相加作为新元素的权重。
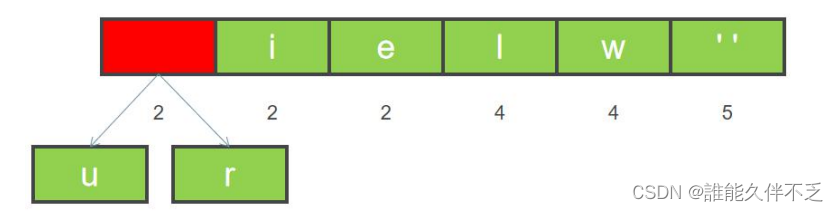
3.新节点加入后,依据权重重新排序,按照权重从小到大排列,上图已有序。
4.红色区域的新增元素可以继续和 i 合并,如下图所示:
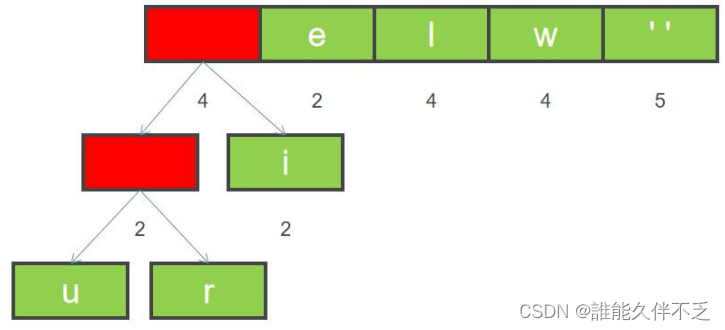
5. 合并节点后, 按照权重从小到大排列,如下图所示。

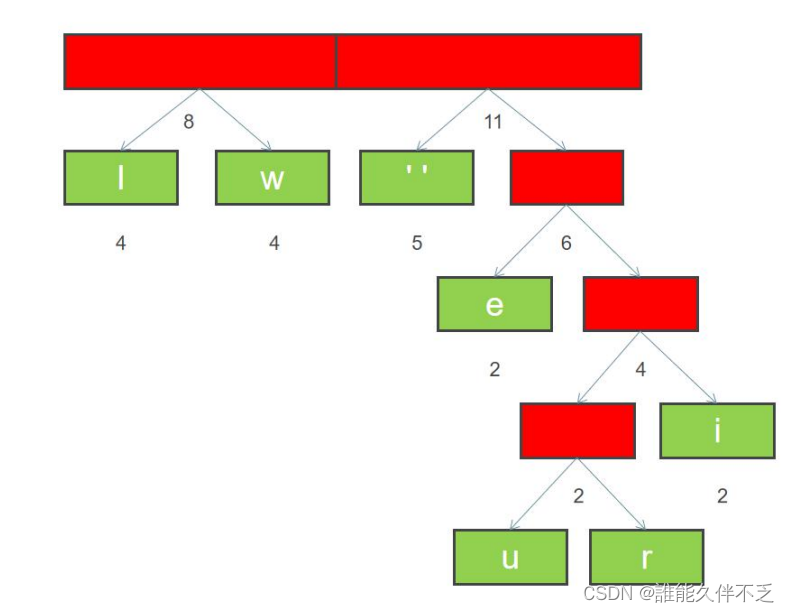
6. 排序后,继续合并最左边两个节点,构建二叉树,并且重新计算新节点的权重
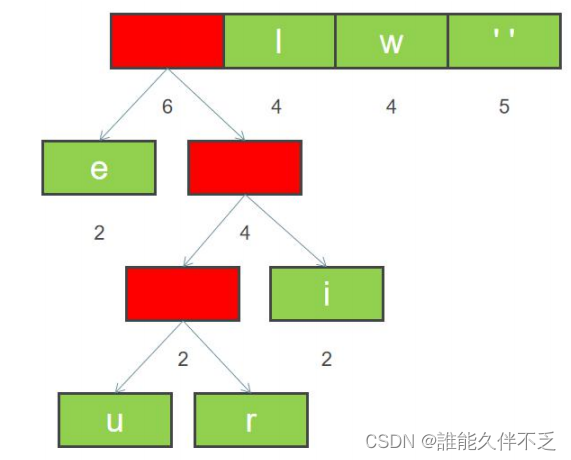
7. 重新排序

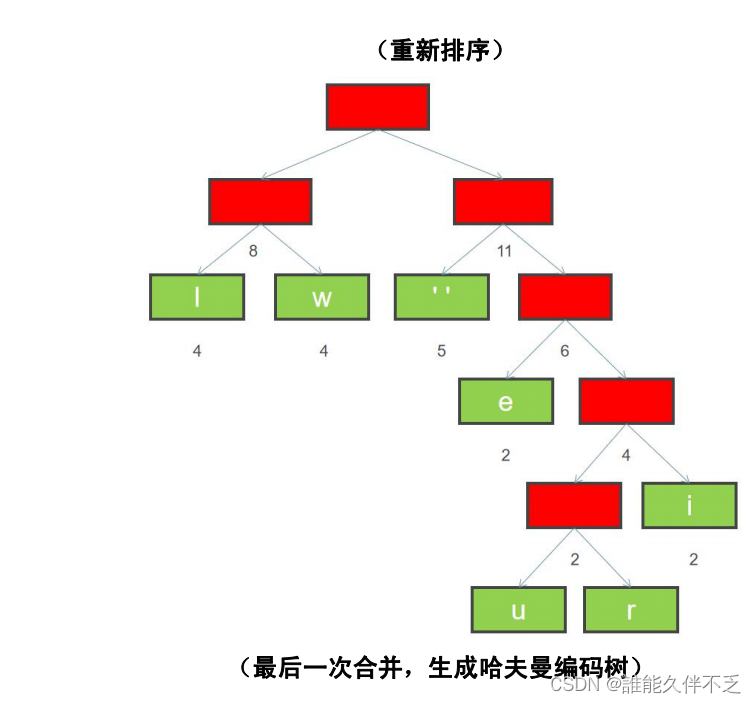
8. 重复上面步骤 6 和 7,直到所有字符都变成二叉树的叶子节点
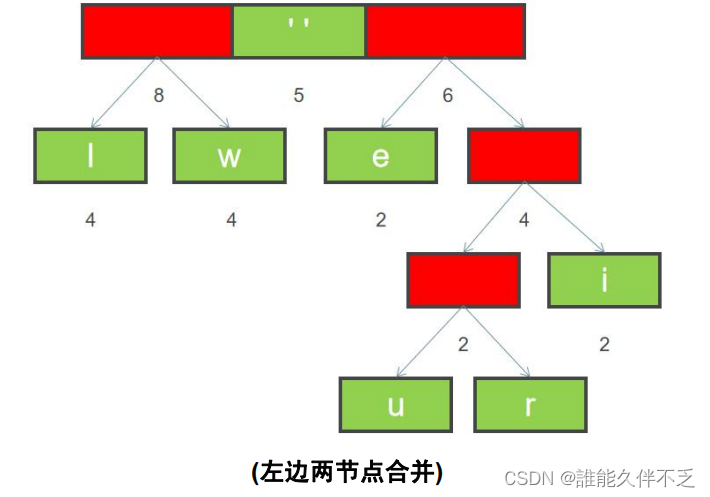
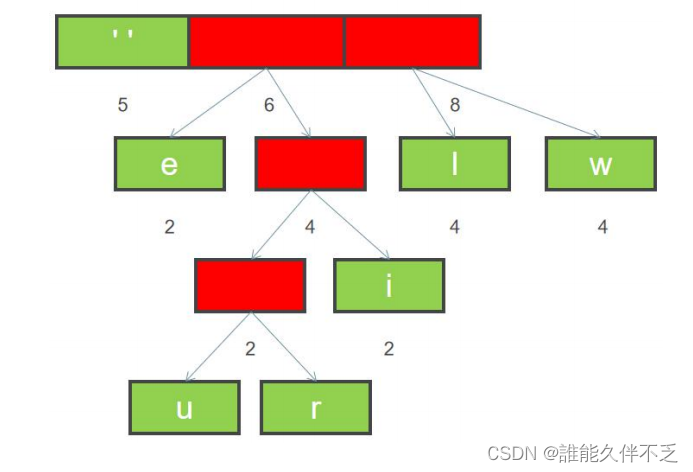
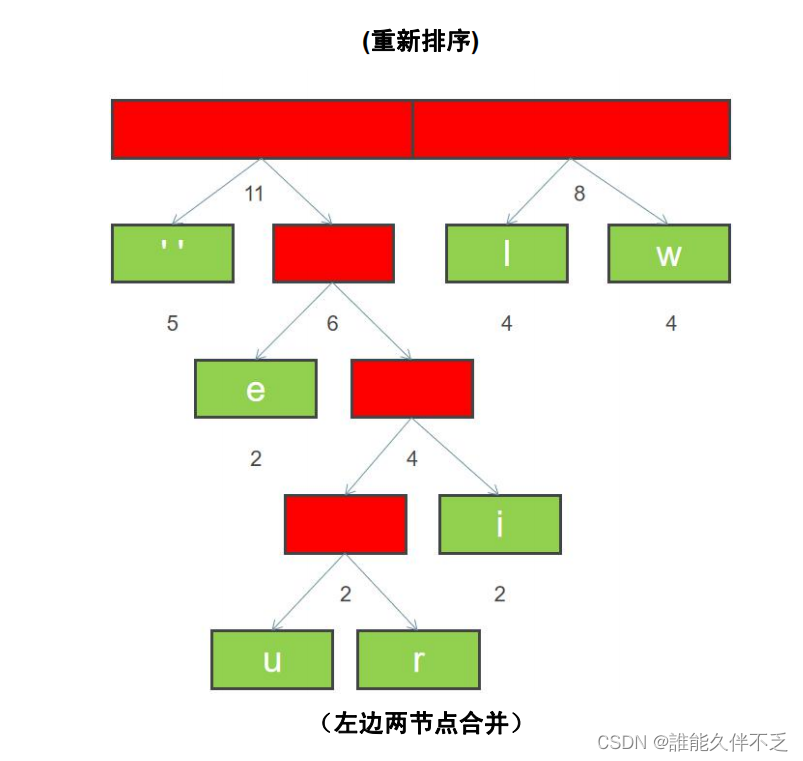
二.具体代码实现
Huff.h
#pragma once
#pragma once
#include <stdio.h>
#include <assert.h>
#include <Windows.h>
#include <iostream>
#include <iomanip>
using namespace std;
#define MaxSize 1024 //队列的最大容量
typedef struct _Bnode
{
char value;
int weight;
struct _Bnode* parent;
struct _Bnode* lchild;
struct _Bnode* rchild;
} Btree, Bnode; /* 结点结构体 */
typedef Bnode* DataType; //任务队列中元素类型
typedef struct _QNode { //结点结构
int priority; //每个节点的优先级,数值越大,优先级越高,优先级相同,取第一个节点
DataType data;
struct _QNode* next;
}QNode;
typedef QNode* QueuePtr;
typedef struct Queue
{
int length; //队列的长度
QueuePtr front; //队头指针
QueuePtr rear; //队尾指针
}LinkQueue;
//队列初始化,将队列初始化为空队列897943840118979438401111
void InitQueue(LinkQueue* LQ)
{
if (!LQ) return;
LQ->length = 0;
LQ->front = LQ->rear = NULL; //把对头和队尾指针同时置 0
}
//判断队列为空
int IsEmpty(LinkQueue* LQ)
{
if (!LQ) return 0;
if (LQ->front == NULL)
{
return 1;
}
return 0;
}
//判断队列是否为满
int IsFull(LinkQueue* LQ)
{
if (!LQ) return 0;
if (LQ->length == MaxSize)
{
return 1;
}
return 0;
}
//入队,将元素 data 插入到队列 LQ 中
int EnterQueue(LinkQueue* LQ, DataType data, int priority) {
if (!LQ) return 0;
if (IsFull(LQ)) {
cout << "无法插入元素 " << data << ", 队列已满!" << endl;
return 0;
}
QNode* qNode = new QNode;
qNode->data = data;
qNode->priority = priority;
qNode->next = NULL;
if (IsEmpty(LQ)) {//空队列
LQ->front = LQ->rear = qNode;
}
else {
qNode->next = LQ->front;
LQ->front = qNode;
//LQ->rear->next =qNode;//在队尾插入节点 qNode
//LQ->rear = qNode; //队尾指向新插入的节点
}
LQ->length++;
return 1;
}
//出队,遍历队列,找到队列中优先级最高的元素 data 出队
int PopQueue(LinkQueue* LQ, DataType* data) {
QNode** prev = NULL, * prev_node = NULL;//保存当前已选举的最高优先级节点上一个节点的指针地址。
QNode* last = NULL, * tmp = NULL;
if (!LQ || IsEmpty(LQ)) {
cout << "队列为空!" << endl;
return 0;
}
if (!data) return 0;
//prev 指向队头 front 指针的地址
prev = &(LQ->front);
//printf("第一个节点的优先级: %d\n", (*prev)->priority);
last = LQ->front;
tmp = last->next;
while (tmp) {
if (tmp->priority < (*prev)->priority) {
//printf("抓到个更小优先级的节点[priority: %d]\n",tmp->priority);
prev = &(last->next);
prev_node = last;
}
last = tmp;
tmp = tmp->next;
}
*data = (*prev)->data;
tmp = *prev;
*prev = (*prev)->next;
delete tmp;
LQ->length--;
//接下来存在 2 种情况需要分别对待
//1.删除的是首节点,而且队列长度为零
if (LQ->length == 0) {
LQ->rear = NULL;
}
//2.删除的是尾部节点
if (prev_node && prev_node->next == NULL) {
LQ->rear = prev_node;
}
return 1;
}
//打印队列中的各元素
void PrintQueue(LinkQueue* LQ)
{
QueuePtr tmp;
if (!LQ) return;
if (LQ->front == NULL) {
cout << "队列为空!";
return;
}
tmp = LQ->front;
while (tmp)
{
cout << setw(4) << tmp->data->value << "[" << tmp->priority << "]";
tmp = tmp->next;
}
cout << endl;
}
//获取队首元素,不出队
int GetHead(LinkQueue* LQ, DataType* data)
{
if (!LQ || IsEmpty(LQ))
{
cout << "队列为空!" << endl;
return 0;
}
if (!data) return 0;
*data = LQ->front->data;
return 1;
}
//清空队列
void ClearQueue(LinkQueue* LQ)
{
if (!LQ) return;
while (LQ->front) {
QueuePtr tmp = LQ->front->next;
delete LQ->front;
LQ->front = tmp;
}
LQ->front = LQ->rear = NULL;
LQ->length = 0;
}
//获取队列中元素的个数
int getLength(LinkQueue* LQ) {
if (!LQ) return 0;
return LQ->length;
}
main.cpp
#include "Huff.h"
using namespace std;
void PreOrderRec(Btree* root);
/* 构造哈夫曼编码树 */
void HuffmanTree(Btree*& huff, int n)
{
LinkQueue* LQ = new LinkQueue;
int i = 0;
//初始化队列
InitQueue(LQ);
/* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */
for (i = 0; i < n; i++)
{
Bnode* node = new Bnode;
cout << "请输入第" << i + 1 << "个字符和出现频率: " << endl;
cin >> node->value; //输入字符
cin >> node->weight;//输入权值
node->parent = NULL;
node->lchild = NULL;
node->rchild = NULL;
EnterQueue(LQ, node, node->weight);
}
PrintQueue(LQ);
//system("pause");
//exit(0);
do {
Bnode* node1 = NULL;
Bnode* node2 = NULL;
if (!IsEmpty(LQ)) {
PopQueue(LQ, &node1);
printf("第一个出队列的数:%c, 优先级: %d\n", node1->value,
node1->weight);
}
else {
break;
}
if (!IsEmpty(LQ)) {
Bnode* node3 = new Bnode;
PopQueue(LQ, &node2);
printf("第二个出队列的数:%c, 优先级: %d\n", node2->value,
node2->weight);
node3->lchild = node1;
node1->parent = node3;
node3->rchild = node2;
node2->parent = node3;
node3->value = ' ';
node3->weight = node1->weight + node2->weight;
printf("合并进队列的数:%c, 优先级: %d\n", node3->value,
node3->weight);
EnterQueue(LQ, node3, node3->weight);
}
else {
huff = node1;
break;
}
} while (1);
}
/************************
* 采用递归方式实现前序遍历
*************************/
void PreOrderRec(Btree* root)
{
if (root == NULL)
{
return;
}
printf("- %c -", root->value);
PreOrderRec(root->lchild);
PreOrderRec(root->rchild);
}
int main(void) {
Btree* tree = NULL;
HuffmanTree(tree, 7);
PreOrderRec(tree);
system("pause");
return 0;
}