目录

引言       

        

什么是数据，结构和算法

时间复杂度的概念

如何计算时间复杂度

   总结

---

引言       

        

        hello大家好，我是boooooom君家宝。在前期的博客中博主呢对c语言的一些重要知识点进行了讲解，接下来博主的博客内容将为大家呈现的是数据结构算法的知识讲解，纯c语言版本。由于c语言对于数据结构和算法的进阶知识不是非常的契合，所以暂时只用c语言呈现初阶的数据结构算法内容，后续博主将会讲解c++的知识点，然后就是我们进阶的数据结构内容了。

什么是数据，结构和算法

        既然开始学习数据结构，那么到底什么是数据结构呢？数据结构是计算机存储、组织数据的方式，指相互之间存在一种或多种特定关系的数据元素的集合。

        那什么又是算法呢？算法就是定义良好的计算过程，它取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法那就是一系列的计算步骤，用来将输入数据转化成输出结果。

时间复杂度的概念

        算法在编写成可执行程序后，运行时需要耗费时间资源和空间（内存）资源。一个算法的好坏就是看一个算法的效率怎么样，而判定一个算法的效率是否高效，就是他的算法复杂度决定的，分为时间复杂度和空间复杂度。今天博主为大家带来的就是时间复杂度的知识点讲解。

        有的小伙伴就会说，是不是电脑算得越快这个算法就更好呢？这个说法是不准确的，例如我的电脑配置很一般，我跑一个qsort快速排序比我一个朋友最顶级的电脑配置跑一个冒泡排序使用的时间还要长一些，那难道就可以说，快速排序这个算法比不上冒泡排序吗？所以评判一个算法的好坏还是得去计算复杂度。

        什么是时间复杂度？在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间，一个算法执行所耗费的时间，从理论上说，是不能算出的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这样很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例。算法中的基本操作的执行次数，为算法的时间复杂度。

        即：找到某条算法语句与问题规划N之间的数学表达式，就是算出了该算法的时间复杂度。

       

如何计算时间复杂度

                时间复杂度的计算，相当于计算算法到底处于什么量级，什么level。现在博主举几个实例，然后分别去计算它们的时间复杂度是多少

Func1：

       这个例子中，上面两层for循环会执行n*n的次数，第三个for循环的执行次数是2n，while循环里的执行次数是10次。所以这个例子的总执行次数就是n^2+2n+10。这个相比大家应该都能算出来，那么他的时间复杂度的表示方法应该写成O(N^2)。这个复杂度不需要你去算得非常的精确，而是去算一个渐进表达法，就是谁对这个表达式起决定性的意义，也就是变化速度最快的那一项。毫无疑问，在这一个表达式当中，取决定性的那一项就是N^2，所以时间复杂度就是O(N^2)。

Func2：

        这个例子依然很简单，很轻松的就能算出来准确的计算次数是2n+10.那么他的时间复杂度是不是就是取决定性的那项也就是2n，所以复杂度就是O(2n)呢？答案是不对的，按照时间复杂的一个计算规则来看，实际上他的复杂度应该是O(N).他的变化量级就是在n的一次方这个量级，所以我们以后遇到什么2n,3n,5n,6n+1之类的，他们复杂度都是O(N)。

Func3：

        这个例子的时间复杂度就是O(M+N)，因为我们并不能很明确的区分M,N这俩到底谁对这个结果的影响更大，除非题目明确说明谁远大于谁，那我们才会舍弃掉其中一个。那如果他还有几个常数项的加减呢，那我们是否要去掉这个常数项？答案是肯定的。

Func4：

        在这个例子中，我们计算出来答案应该是100，是一个常数，那他的时间复杂度我们就应该写成O(1)。换句话说，只要是计算结果为常数项，那他的时间复杂度就都是O(1)。请注意，这个O(1)的意思不是说只有一次，而是代表常数次。

Func5：

        首先，strchr是一个库函数，相当于是在一个字符数组中查找一个字符，那么这个时间复杂度是多少呢？答案是O(N)。为什么是O(N)呢，这个算法他有很多种情况，最好的情况就是我们第一次查找就找到了，最坏的结果就是最后一个才找到或者说根本找不到，那么我们应该以哪一种情况来定义复杂度呢？那肯定是以最坏的情况来定义嘛，所以这道题目，最好的情况就是1次，最差的结果是N次。所以时间复杂度就是O(N)。时间复杂度预算，是一个稳健保守预期。

Func6：

        这个例子呢是一个冒泡排序，就是从(n-1),(n-2),(n-3)...一直加在一起嘛，所以就是一个等差数列的求和，算下来就是(n-1)*n/2，所以他的时间复杂度就是O(N^2).

Func7：二分查找

        这是一个二分查找，我们先回复一下二分查找的思想，二分查找的前提是这个数列是有序的，我们先从这个数列的中间部分查找，如果需要查找的数比中间值大，我们就定位到左边区域，接下来再直接找到左边那一半区域的中间，去和需要查找的数进行对比，以此反复不断折半缩小范围直到最后找到目标或者确定目标数不在数列里。如图：

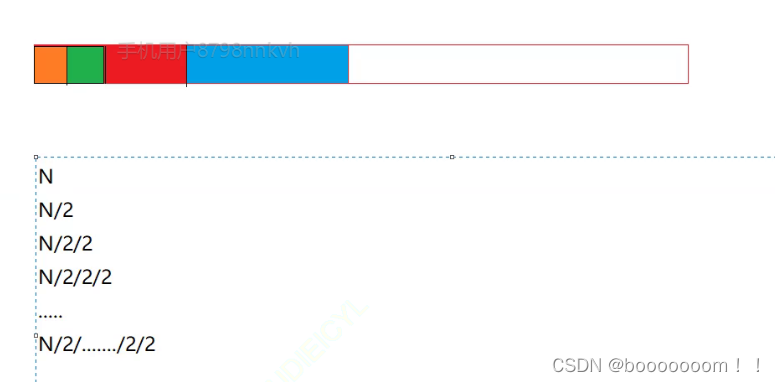        同理，这个也会有很多情况，那我们直接定位到什么时候是最坏的情况，也就是将区间缩放到只剩一个值时是最坏情况。要么这一个值就是目标值，要么就确定目标值不在数列里。那这个最坏情况我们不妨设它查找了X次，那么2^X=N, X=log以2为底N的对数。但是各位也能看得出来博主对这样的一个情况实在不方便用键盘打印出来，所以我们会把这样以2为底的一种情况的复杂度记为O(logN),那有些朋友就要疑问了，如果是以3为底或者以4为底呢？那样的话就只能老老实实写出来了，不过这种复杂度的算法很少很少，例如以3为底的有后续博主会讲到的b树，其他的基本是没有看到过其他底数的复杂度了。

   总结

        算法有无数多种类，博主也不能一一列举出来然后计算出它的时间复杂度，例如AVL树，红黑树等，不过从这几种情况大概我们已经回去计算所有的算法复杂度了，而且博主的建议就是在我们计算过某些常用的算法，例如冒泡排序，快速排序，二分查找等，我们可以把它记住他的复杂度是多少，以后面试的时候做一些oj类的题目他们会要求复杂度得控制在一定的范围之类，所以我们就需要先确定好复杂度之后再去敲代码。