一 点睛

左偏树（leftist tree 或 leftist heap）也叫作左偏堆、左倾堆、左式堆，是计算机科学中的一种树，也是一种优先队列实现方式，属于可并堆，在信息学中十分常见，在统计、最值、模拟、贪心等类型的题目中应用广泛。

左偏树并不是平衡树，它不是为了快速访问节点而设计的，可以快速访问最大（或最小）节点，并在树中修改后快速合并。左偏树合并操作的时间复杂度在最坏情况下为O(logn )，完全二叉堆合并操作的时间复杂度在最坏情况下为O (n )，所以左偏树更适用于合并操作的情形。

二 堆、优先队列、可合并堆和左偏树的区别

堆：可以被看作一棵完全二叉树的顺序存储结构，在这棵完全二叉树中，若每个节点的值都大于或等于左右子节点的值，则称之为最大堆；若每个节点的值都小于或等于左右子节点的值，则称之为最小堆。

优先队列：利用堆来实现的，取得最大值（或最小值）需要O(1)时间，删除最大值（或最小值）需要O (logn )时间，插入元素也需要O (logn )时间。

可合并堆：支持合并操作的堆，除了支持优先队列的三种基本操作，还支持合并操作。

左偏树：是一棵有堆序性和左偏性的二叉树，是一种可合并堆的实现。

三  左偏树的性质

1 堆序性

节点的值大于或等于（或小于或等于）其左右子节点的值。对最大堆，父节点大、子节点小，即key(i)≤key(parent(i))（注意：左偏树只有键值大小满足堆序性质，不再满足完全二叉树的结构性质）。每个节点的值都大于或等于其左右子节点的值，如下图所示。

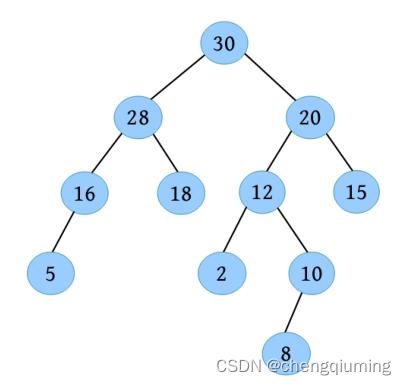
2 左偏性

左偏性指“向左偏”。节点的左子节点的距离大于或等于右子节点的距离。左偏树的节点除了和二叉树的节点一样有左右子树，还有两个属性：外节点和距离。

• 外节点：节点 i 的左子树或右子树为空时，节点 i 被称为外节点。

• 距离：节点 i 的距离指节点 i 到它的后代中最近的外节点所经过的边数。特别地，若节点 i 自身是外节点，则它的距离为 0；空节点的距离为 -1。左偏树的距离指树根到最近的外节点所经过的边数。

一棵左偏树如下图所示，树根到最近外节点的距离为 2，因此该左偏树的距离为2。

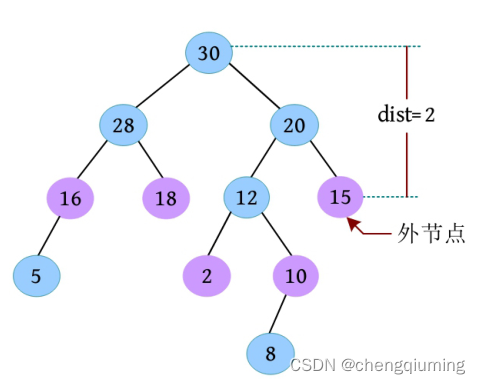
左偏树有左偏性，每个节点的左子节点的距离都大于或等于右子节点的距离，dist(lc(i))≥dist(rc(i))。

左偏性是以距离衡量的，并不意味着左子树的树高大于或等于右子树的树高。

3 节点的距离等于它的右子节点的距离加 1

因为左偏性保证每个节点的左子节点的距离都大于或等于右子节点的距离，而节点的距离等于最近外节点的距离，因此节点的距离等于右子节点的距离加1：dist(i)=dist(rc(i))+1。

4 n 个节点的左偏树距离最多为 log(n+1)-1

四 左偏树的基本操作之合并

左偏树的基本操作包括合并根节点、删除根节点、插入节点和创建左偏树等。

1 合并

左偏树的合并操作是其他操作的基础，该操作需要满足左偏树的两个基本性质。如下图所示，假设两个左偏树的树根分别为a、b，则合并这两棵左偏树的步骤如下。

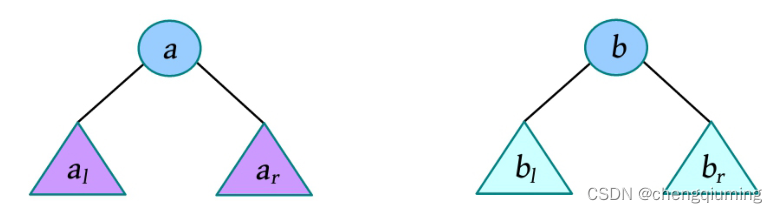
（1）比较 a、b 的关键字，若 key(a)≤key(b)，则交换两棵左偏树，保证最大堆的堆序性。

（2）合并 a 的右子树与以 b 为根的左偏树，将合并后的左偏树作为 a 的右子树。

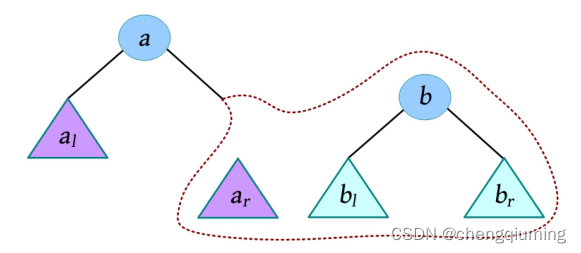
（3）比较 a 的左右子树距离，若左子树的距离小于右子树，则交换。然后更新 a 的距离为右子树的距离加 1。

2 图解

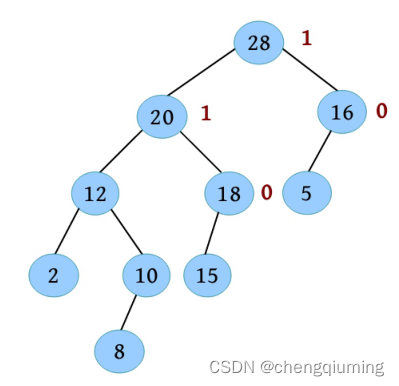
两棵左偏树如下图所示，合并两棵左偏树的过程如下。

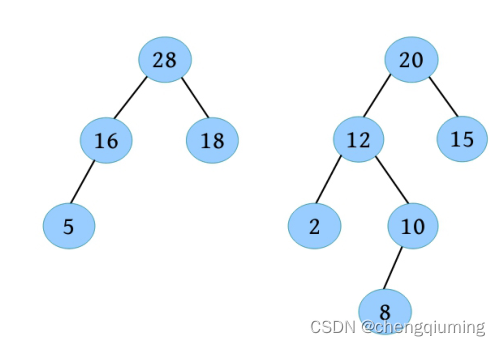
（1）比较树根的关键字，28>20，无须交换。

（2）合并 28 的右子树与以 20 为根的左偏树。

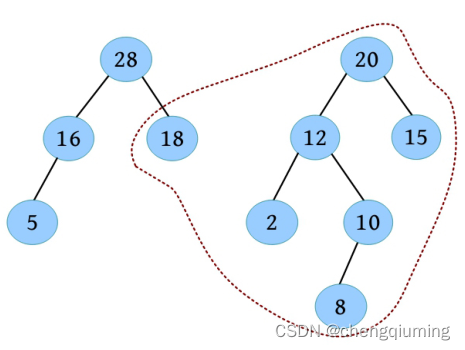
（3）比较树根的关键字 18 和 20，18<20，交换两棵左偏树。

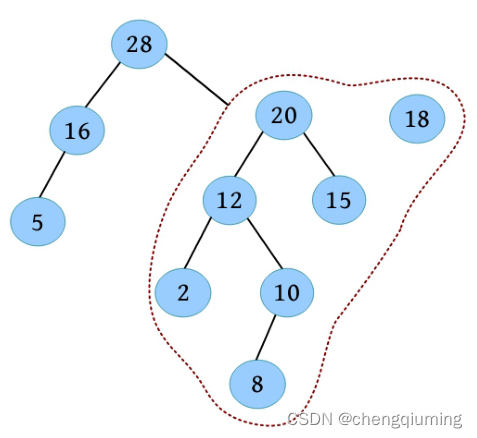
（4）合并 20 的右子树与以 18 为根的左偏树。

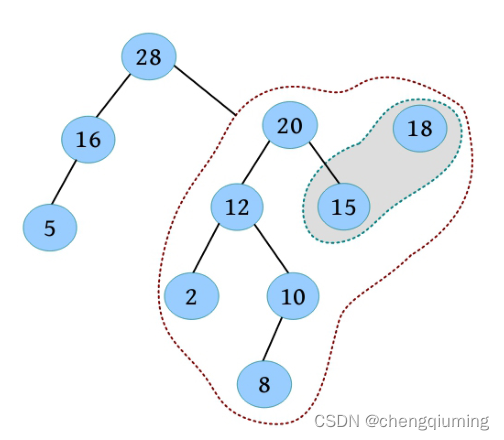
（5）比较树根的关键字 15 和 18，15<18，交换两棵左偏树。

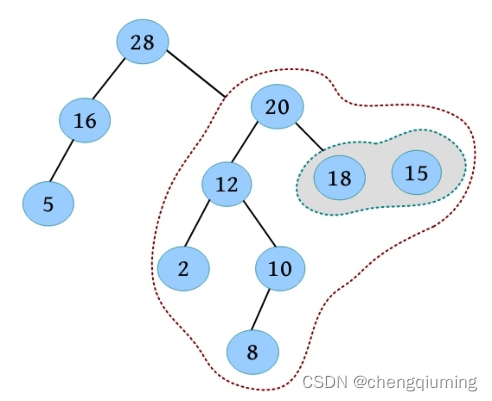
（6）合并 18 的右子树与以 15 为根的左偏树。18 的右子树为空，15 作为 18 的右子树。

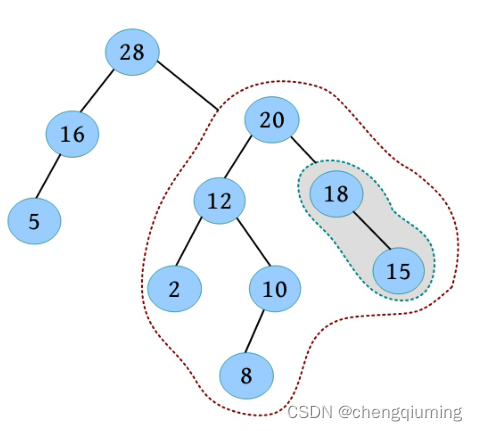
（7）比较 18 的左右子树距离，左子树的距离小于右子树的距离，左右子树交换。然后更新 18 的距离为其右子树的距离加 1，其右子树为空，距离为 -1，因此 18 的距离为 0。

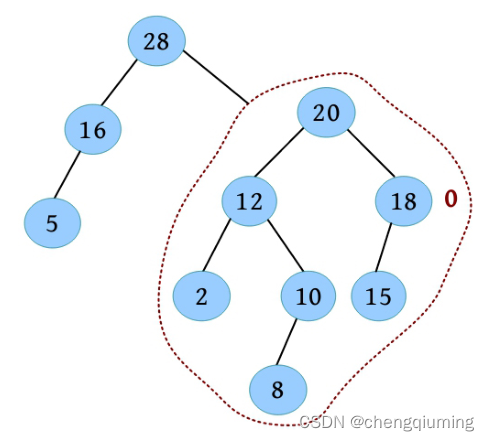
（8）比较 20 的左右子树距离，左子树的距离大于右子树，无须交换。然后更新 20 的距离为其右子树的距离加 1，20 的距离为 1。

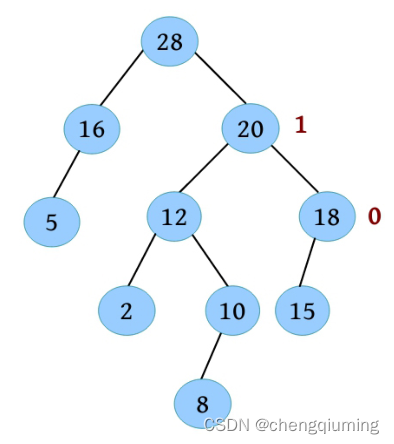
（9）比较 28 的左右子树距离，左子树的距离小于右子树，左右子树交换。然后更新 28 的距离为右子树的距离加 1，28 的距离为 1。

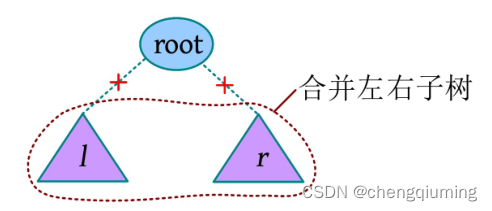
五 左偏树的基本操作之删除

删除根节点时只需将左右子树的父节点修改为自己，然后合并左右子树即可。删除根节点（最大或最小节点）是基于合并操作的，其时间复杂度为O (logn )。

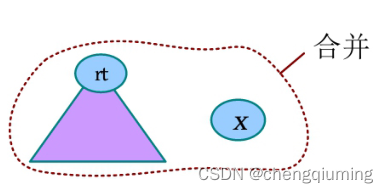
六 左偏树的基本操作之插入节点

插入一个新节点，首先创建一棵只包含一个新节点的左偏树，然后和原树合并。插入是基于合并操作的，其时间复杂度为O (logn )。

七 左偏树的基本操作之创建左偏树

1 创建一棵左偏树时有两种方法

① 将每个节点都依次插入，每次插入的时间复杂度都为O (logn)，总的时间复杂度为O (nlogn )；

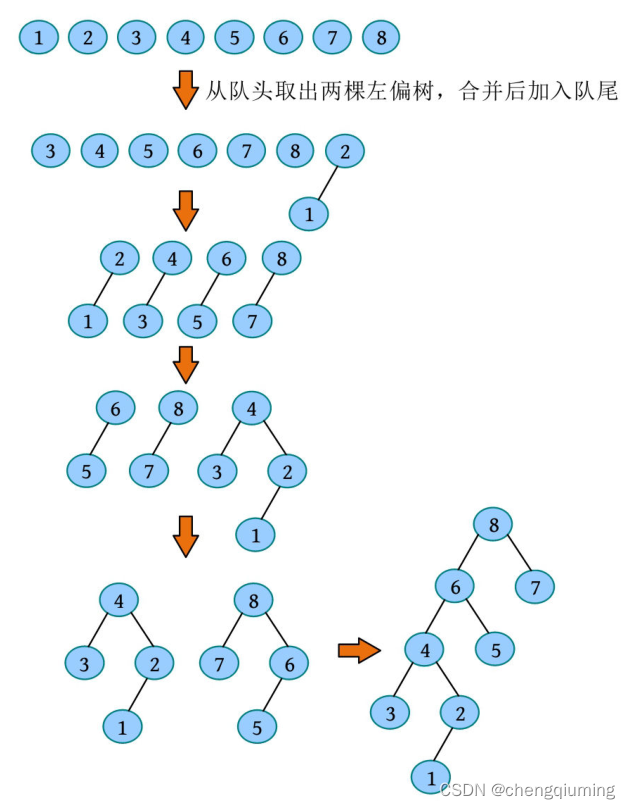
② 两两合并，将 n 个节点放入先进先出队列，依次从队头取出两棵左偏树，合并后加入队尾，直到只剩下一棵左偏树，其时间复杂度为O(n)。

2 图解

输入序列 1, 2, 3, 4, 5, 6, 7, 8，构建一棵左偏树，其过程如下图所示。