文章目录
- 前言
- 一、二分查找
- 1、正常二分
- 2、二分找第一个出现要查找的数的位置
- 3、在旋转数组中找最小数字
- 二分总结
- 一、归并排序
- 1、正常归并
- 2、小和问题
- 归并总结
前言
之前我们学习了各种排序算法,今天来让我们看看在线OJ上的题目吧,有哪些排序算法有什么样的延深吧。
一、二分查找
1、正常二分
查找有序数组中的数字,这是二分查找最常规的操作。
void Search()
{
int tmp[] = { -1,0,3,5,9,12 };
int sz = sizeof(tmp) / sizeof(tmp[0]);
int left = 0;
int right = sz - 1;
int target = 9;//要查找的值
int pos = -1;//查找值的位置
while (left <= right)
{
int mid = left + ((right - left) >> 1);
if (target < tmp[mid])
{
right = mid - 1;
}
else if (target > tmp[mid])
{
left = mid + 1;
}
else
{
pos = mid;
break;
}
}
printf("pos = %d\n", pos);
}
void test()
{
Search();
}
int main()
{
test();
return 0;
}
思路:

点这里进入推荐练习哟
2、二分找第一个出现要查找的数的位置
在有重复元素且有序的数组中查找我们所要的第一个出现的数的位置,这是在上面得基础上在进行几次二分查找。
void Search()
{
int tmp[] = { 5,6,7,7,7,8,8,10 };
int target = 8;
int sz = sizeof(tmp) / sizeof(tmp[0]);
int left = 0;
int right = sz - 1;
int pos = -1;
while (left <= right)
{
if (tmp[left] == target)//判断左边的值是否是我们第一个要找的值
{
pos = left;
break;
}
int mid = left + ((right - left) >> 1);
if (target <= tmp[mid])//注意要有等号
{
right = mid - 1;
}
else if (target > tmp[mid])
{
left = mid + 1;
}
}
if (tmp[left] == target)
{
pos = left;
}
printf("pos = %d", pos);
}

思路:

注意我们循环后要加一次判断,防止出现漏算的情况!!!
点击这里进入练习哟:这个找到我们第一次出现的数向后进行累加就可以了
点击这里进入练习哟:这个和上面的思路相似哦。
3、在旋转数组中找最小数字
int Search()
{
int tmp[] = { 3, 4, 5, 1, 2 };
int left = 0;
int right = sizeof(tmp) / sizeof(tmp[0]) - 1;
while (left < right)
{
int mid = left + ((right - left) >> 1);
if (tmp[mid] < tmp[right])
{
right = mid;
}
else if (tmp[mid] > tmp[right])
{
left = mid + 1;
}
else
{
right -= 1;
}
}
printf("%d\n", tmp[left]);
}
void test()
{
Search();
}
int main()
{
test();
return 0;
}

思路:

我们通过数组中的区间关系来定位最小值的位置。
点击这里进入练习哟:这个使用三次二分就可以找到了
二分总结
我们使用二分不仅可以在有序数组中,只要符合我们一次可以去掉一般元素,符合我们二分思想就可以用我们的二分查找。我们查找波峰和波谷也可以通过二分来进行完成。
一、归并排序
1、正常归并
void MergeSort(int* nums, int left, int right,int *tmp)
{
if (left >= right)
{
return;
}
//把区间拆分为两段
int middle = (left + right) >> 1;
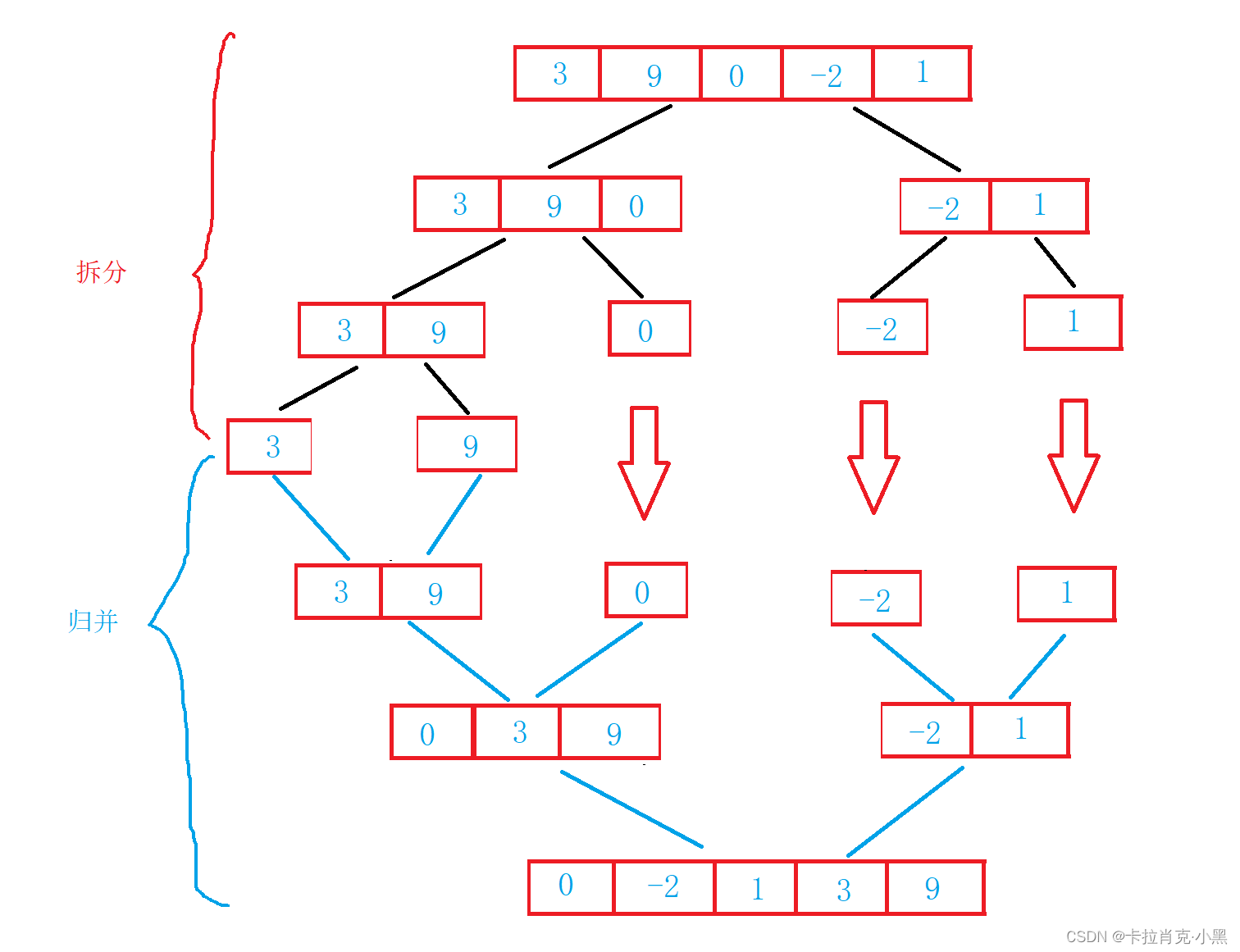
//拆分
MergeSort(nums, left, middle, tmp);
MergeSort(nums, middle+1, right, tmp);
//归并
int begin1 = left;
int begin2 = middle + 1;
int end1 = middle;
int end2 = right;
int i = 0;
//和链表的链接差不多
//直到有一个区间结束结束循环
while ((begin1 <= end1) && (begin2 <= end2))
{
//那个值小那个值进入开辟的数组
if (nums[begin1] <= nums[begin2])
{
tmp[i++] = nums[begin1++];
}
else
{
tmp[i++] = nums[begin2++];
}
}
//找到未完全结束的数组,并且把数组中的元素尾加到开辟的数组中
while (begin1 <= end1)
{
tmp[i++] = nums[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = nums[begin2++];
}
//把开辟的数组中的内容拷贝到源数组中
//拷贝时要注意拷贝时的位置
memcpy(nums + left, tmp, (right - left + 1) * sizeof(int));
}
2、小和问题
例如,数组 s = [1, 3, 5, 2, 4, 6] ,在 s[0] 的左边小于或等于 s[0] 的数的和为 0 ; 在 s[1] 的左边小于或等于 s[1] 的数的和为 1 ;在 s[2] 的左边小于或等于 s[2] 的数的和为 1+3=4 ;在 s[3] 的左边小于或等于 s[3] 的数的和为 1 。
int minSum(int* tmp, int left, int right) {
if (left == right)
{
return 0;
}
int mid = (left + right) / 2;
//进行区间划分
return minSum(tmp, left, mid)
+ minSum(tmp, mid + 1, right)
+ merge(tmp, left, mid, right);
}
int merge(int* tmp, int left, int mid, int right)
{
int n = right - left + 1;
int* help = (int*)malloc(sizeof(int)*n);//开辟辅助空间
int index = 0;
int p1 = left;
int p2 = mid + 1;
long long sum = 0;
//进行归并并计算小和
while (p1 <= mid && p2 <= right)
{
if (tmp[p1] <= tmp[p2])
{
sum += (right - p2 + 1) * tmp[p1];//计算小和
help[index++] = tmp[p1++];
}
else
{
help[index++] = tmp[p2++];
}
}
while (p1 <= mid)
{
help[index++] = tmp[p1++];
}
while (p2 <= right)
{
help[index++] = tmp[p2++];
}
for (int i = 0; i < n; i++)
{
tmp[left + i] = help[i];
}
return sum;
}
void test()
{
//Search();
int tmp[] = { 1, 3, 5, 2, 4, 6 };
int sz = sizeof(tmp) / sizeof(tmp[0]);
int sum = minSum(tmp, 0, sz - 1);
printf("%d\n", sum);
}
int main()
{
test();
return 0;
}

思路:
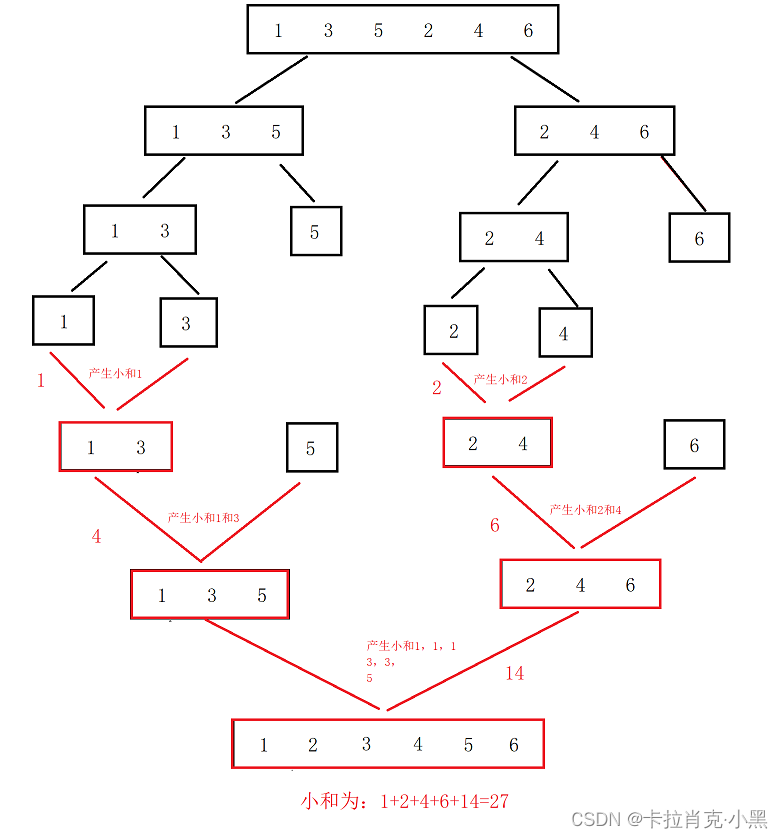
我们在归并的同时计算右区间有几个元素大于次元素,这样归并就可计算出小和了
题目练习
归并总结
我们还可以用归并算出逆序对的个数,思路和小和问题一样,在归并过程中顺便解决问题。