一. 斐波那契数列模型

解题步骤：

1. 确定状态表示（最重要）：明确dp表里的值所表示的含义
2. 推导状态转移方程（最难）：dp[i] 等于什么？
3. 初始化：保证填表的时候不越界
4. 填dp表：通过前面已经计算过的状态来推导当前状态的值
5. 返回结果

1. 第 N 个泰波那契数

题目解析
我们对题目给的公式进行转化：

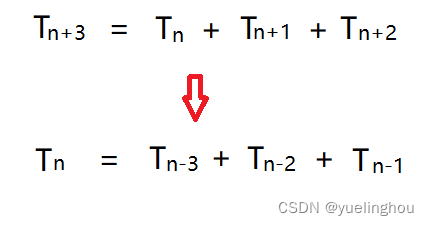
观察公式可以看到，如果要求第 i 个泰波那切数的话，我们只需知道前 i-1、i-2、i-3 的值即可。

算法原理

• 状态表示：dp[i] 代表第 i 个泰波那切数
• 状态转移方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
• 初始化：dp[0] = 1、dp[1] = 1、dp[2] = 1
• 填表：根据状态转移方程和初始化的值，使用滑动窗口的方式一直计算最终得到第 i 个泰波那切数。
• 返回值：第 n 个泰波那切数

编写代码

class Solution {
public:
    int tribonacci(int n) 
    {
        // 1、建表
        // 2、初始化
        // 3、填表
        // 4、返回值

        vector<int> dp(n+1);

        dp[0] = 0, dp[1] = dp[2] = 1;

        for(int i = 3; i <= n; ++i)
        {
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
        }

        return dp[n];
    }
};

/*
- 时间复杂度：O(n)
- 空间复杂度：O(n)
*/

2. 三步问题

---

题目解析：小孩最多一次跳三步，假设要跳到第n级台阶，那最后跳到第n级台阶时的那一步一定是下面三种情况之一：

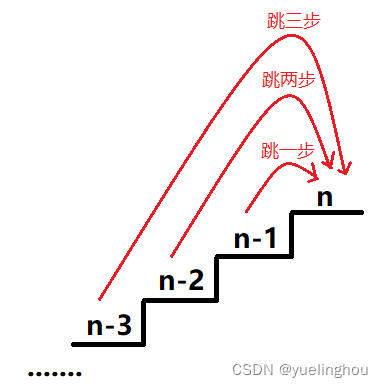
所以想求跳到第n级台阶有几种方法的话，我们只需知道跳到第 n-1、n-2 和 n-3 台阶时各自有几种方法，然后把它们相加起来即可。

PS：计算时需要注意取模

算法原理

• 状态表示：dp[i] 表示 到达i位置时，一共有多少种方法。
• 状态转移方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
• 初始化：dp[1] = 1 dp[2] = 2 dp[3] = 4
• 填表顺序：从左往右
• 返回值 ：dp[n]

代码实现

class Solution
{
public:
	int waysToStep(int n)
	{
		// 1、处理特殊情况
		if (n == 1) return 1;
		if (n == 2) return 2;
		if (n == 3) return 4;
		// 2、创建dp表
		vector<int> dp(n + 1);
		// 3、初始化
		dp[1] = 1;
		dp[2] = 2;
		dp[3] = 4;
		// 4、填表
		for (size_t i = 4; i <= n; ++i)
			dp[i] = ((dp[i - 1] + dp[i - 2]) % 1000000007 + dp[i - 3]) % 1000000007;
		// 5、返回值
		return dp[n];
	}
};

/*
- 时间复杂度：O(n)
- 空间复杂度：O(n)
*/

3. 使用最小花费爬楼梯

---

题目解析

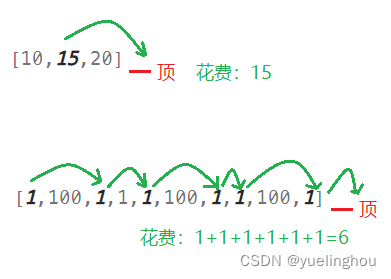
解法一：从左往右填表

• 状态表示：dp[i] 表示到达i位置时的最小花费
• 状态转移方程
  
• 初始化（保证填表的时候不越界）：dp[0]=dp[1]=0
• 填表顺序：从左往右
• 返回值：因为是从0号台阶开始，所以最后一个台阶的下标为 n-1。最后返回 dp[n]

代码实现

class Solution
{
public:
	int minCostClimbingStairs(vector<int>& cost)
	{
		// 创建dp表
		size_t n = cost.size();
		vector<int> dp(n + 1);
		// 填表
		for (size_t i = 2; i <= n; ++i)
			dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
		// 返回值
		return dp[n];
	}
};

/*
- 时间复杂度：O(n)
- 空间复杂度：O(n)
*/

解法二：从右往左填表

• 状态表示：dp[i] 表示从i位置出发，到达楼顶，此时的最小花费

• 状态转移方程
  

• 初始化：dp[n-1] = cost[n-1]、dp[n-2] = cost[n-2]

• 填表顺序：从右往左

• 返回值：min(dp[0]， dp[1])

代码实现

class Solution
{
public:
	int minCostClimbingStairs(vector<int>& cost)
	{
		int n = cost.size();
		vector<int> dp(n);
		dp[n - 1] = cost[n - 1];
		dp[n - 2] = cost[n - 2];
		for (int i = n - 3; i >= 0; --i)
			dp[i] = cost[i] + min(dp[i + 1], dp[i + 2]);
		return min(dp[0], dp[1]);
	}
};

/*
- 时间复杂度：O(n)
- 空间复杂度：O(n)
*/