本文属于数据结构专栏文章，适合数据结构入门者学习，涵盖数据结构基础的知识和内容体系，文章在介绍数据结构时会配合上动图演示，方便初学者在学习数据结构时理解和学习，了解数据结构系列专栏点击下方链接。

---

• 博客主页：Duck Bro 博客主页
• 系列专栏：数据结构专栏
• 关注博主，后期持续更新系列文章
• 如果有错误感谢请大家批评指出，及时修改
• 感谢大家点赞👍收藏⭐评论✍

---

数据结构入门 — 树的概念与结构

本文关键字：数据结构、树、概念、结构

---

---

一、树的概念

树是一种非线性数据结构，由若干个节点和它们之间的联系组成。 树具有如下特点：

1. 树的第一个节点称为根节点，根节点下可以有若干个子节点，每个子节点下也可以有若干个子节点，以此类推。

2. 节点之间的联系称为边，根节点没有父节点，其他节点的父节点是其直接上级，子节点是其直接下级。

3. 每个节点可以有零个或多个子节点，但每个节点只有一个父节点。

4. 树中节点的个数称为节点数或大小，从根节点到任意节点的路径上的边数称为深度或层数。

5. 树可以为空树，即不包含任何节点。

树常用于表示层次结构，例如计算机科学中的文件系统、解析树、表达式树等。在算法中，树是许多高效的数据结构和算法的基础，例如搜索树、堆、红黑树、B树、哈夫曼树等。

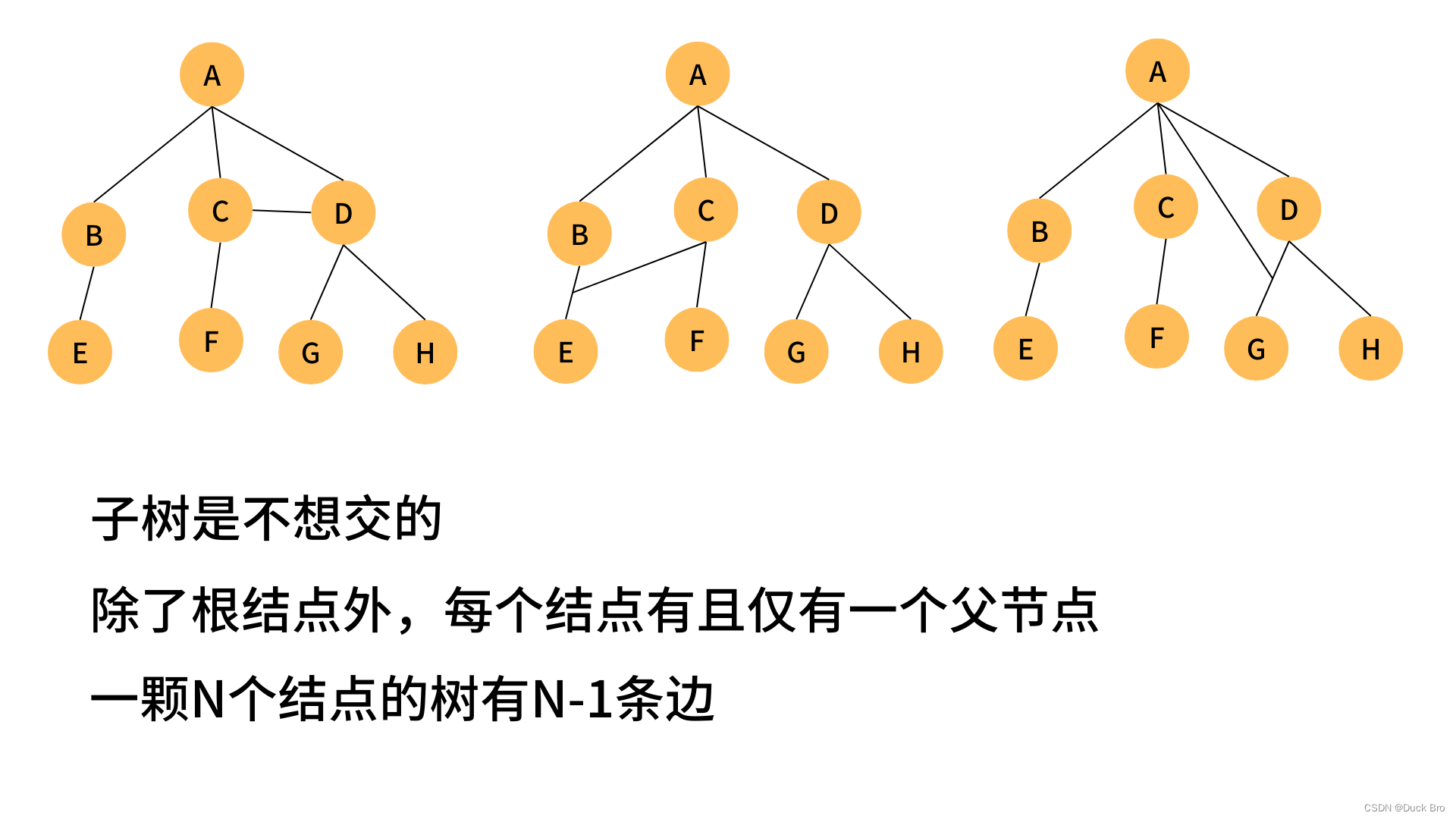
注意：树形结构中，子树之间不能有交集，否则就不是树形结构

---

二、树的结构

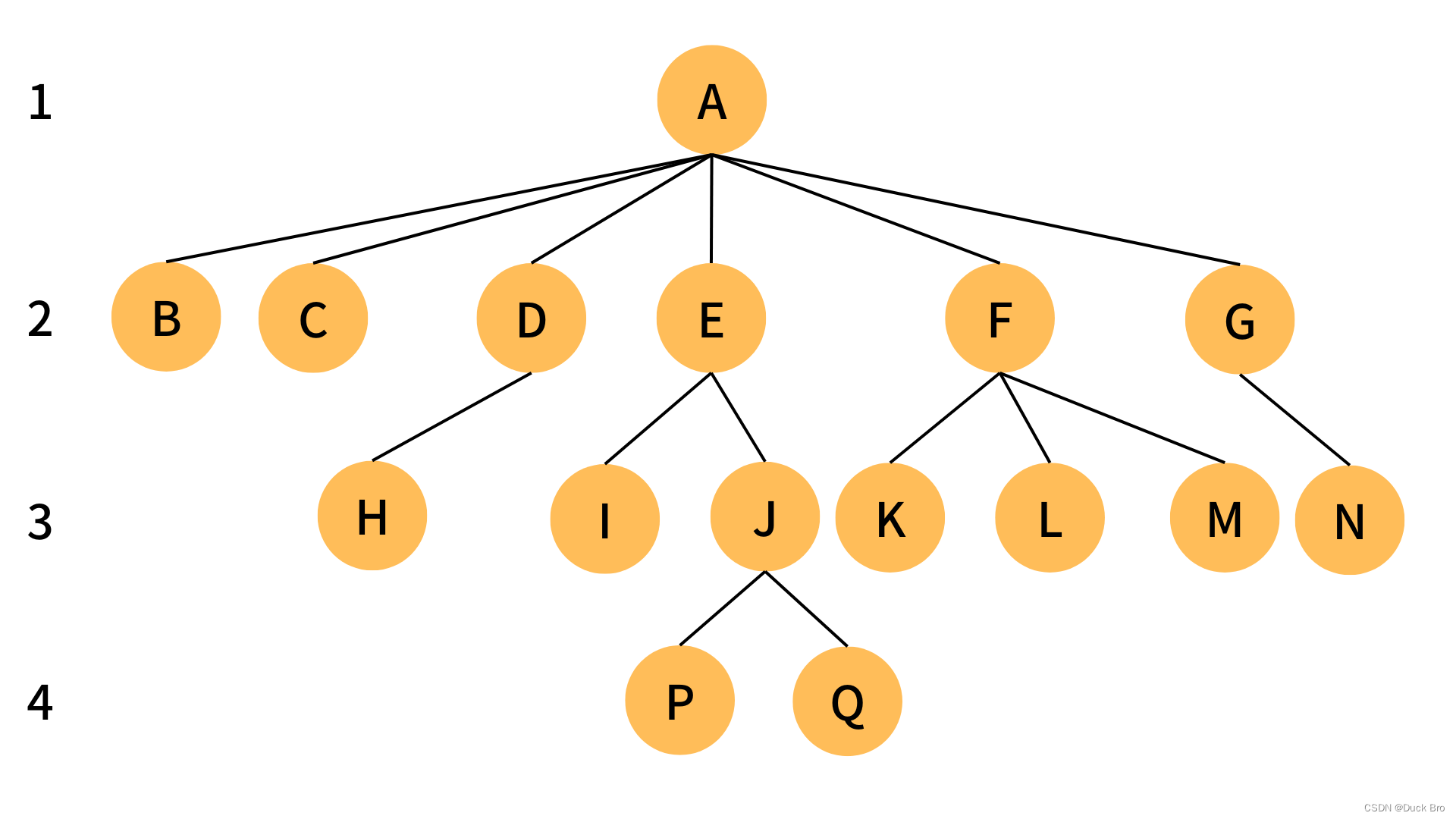
概念	说明	举例
节点的度	一个节点含有的子树的个数称为该节点的度	如上图：A的为6
叶节点或终端节点	度为0的节点称为叶节点	如上图：B、C、H、I…等节点为叶节点
非终端节点或分支节点	度不为0的节点	如上图：D、E、F、G…等节点为分支节点
双亲节点或父节点	若一个节点含有子节点，则这个节点称为其子节点的父节点	如上图：A是B的父节点
孩子节点或子节点	一个节点含有的子树的根节点称为该节点的子节点	如上图：B是A的孩子节点
兄弟节点	具有相同父节点的节点互称为兄弟节点	如上图：B、C是兄弟节点
树的度	一棵树中，最大的节点的度称为树的度	如上图：树的度为6
节点的层次	从根开始定义起，根为第1层，根的子节点为第2层，以此类推	如上图：1、2、3、4
树的高度或深度	树中节点的最大层次	如上图：树的高度为4
堂兄弟节点	双亲在同一层的节点互为堂兄弟	如上图：H、I互为兄弟节点
节点的祖先	从根到该节点所经分支上的所有节点	如上图：A是所有节点的祖先
子孙	以某节点为根的子树中任一节点都称为该节点的子孙	如上图：所有节点都是A的子孙
森林	由m（m>0）棵互不相交的树的集合称为森林

---

三、树的表示

树的常见表示方法有以下几种：

1. 链式前向星表示法：这种方法是树的常见表示方法之一。使用链式前向星构造一个图，其中每个节点表示树中的一个节点，每条边表示节点之间的父子关系。这个方法可以方便地进行遍历操作。

2. 双亲表示法：这种方法是使用一个数组来表示树，数组中每个元素表示树中的一个节点，其值为该节点的值，数组下标表示该节点的编号，而该节点在数组中对应的值表示其双亲节点的编号。这个方法可以方便地查找父节点。

3. 孩子兄弟表示法：这种方法也是使用一个数组来表示树，数组中每个元素表示树中的一个节点，存储每个节点的第一个孩子节点的编号，由此可以找到该节点的所有孩子节点。这个方法可以方便地查找孩子节点。

4. 邻接表表示法：这种方法是使用一个链表数组来表示树，数组中每个元素表示树中的一个节点，链表中存储该节点的所有孩子节点。这个方法可以方便地遍历孩子节点。

我们这里就简单的了解其中最常用的孩子兄弟表示法。

typedef int DataType;
struct Node
{
	 struct Node* _firstChild1; // 第一个孩子结点
	 struct Node* _pNextBrother; // 指向其下一个兄弟结点
	 DataType _data; // 结点中的数据域
};

---

四、树在实际中的运用

树在实际中有很多应用，以下是一些常见的应用场景：

1. 文件系统：文件系统通常使用树来组织文件和文件夹之间的关系。每个文件夹都可以包含子文件夹和文件，形成一棵树。

2. 数据库：数据库中的索引通常采用树的数据结构来存储，以便快速查找和排序数据。

3. 编译器：编译器通常使用抽象语法树（AST）来表示源代码，便于程序分析和优化。

4. 网络协议：许多网络协议使用树来表示分层结构，例如TCP/IP协议中的网络层、传输层和应用层。

5. 人工智能：人工智能中的决策树（Decision Tree）用于分类和预测，神经网络（Neural Network）也是一种树形结构。

6. 算法：许多经典算法（如二叉搜索树、AVL树、红黑树）都使用树的数据结构，以提高算法效率。

---