给你一个正整数数组 nums 。
同时给你一个长度为 m 的整数数组 queries 。第 i 个查询中，你需要将 nums 中所有元素变成 queries[i] 。你可以执行以下操作 任意 次：

将数组里一个元素 增大 或者 减小 1 。
请你返回一个长度为 m 的数组 answer ，其中 answer[i]是将 nums 中所有元素变成 queries[i] 的 最少 操作次数。

注意，每次查询后，数组变回最开始的值。

示例 1：
输入：nums = [3,1,6,8], queries = [1,5]
输出：[14,10]
解释：第一个查询，我们可以执行以下操作：

• 将 nums[0] 减小 2 次，nums = [1,1,6,8] 。
• 将 nums[2] 减小 5 次，nums = [1,1,1,8] 。
• 将 nums[3] 减小 7 次，nums = [1,1,1,1] 。
  第一个查询的总操作次数为 2 + 5 + 7 = 14 。
  第二个查询，我们可以执行以下操作：
• 将 nums[0] 增大 2 次，nums = [5,1,6,8] 。
• 将 nums[1] 增大 4 次，nums = [5,5,6,8] 。
• 将 nums[2] 减小 1 次，nums = [5,5,5,8] 。
• 将 nums[3] 减小 3 次，nums = [5,5,5,5] 。
  第二个查询的总操作次数为 2 + 4 + 1 + 3 = 10 。

示例 2：
输入：nums = [2,9,6,3], queries = [10]
输出：[20]
解释：我们可以将数组中所有元素都增大到 10 ，总操作次数为 8 + 1 + 4 + 7 = 20 。

提示：
n == nums.length
m == queries.length
1 <= n, m <= 105
1 <= nums[i], queries[i] <= 109

题目链接在：题目链接

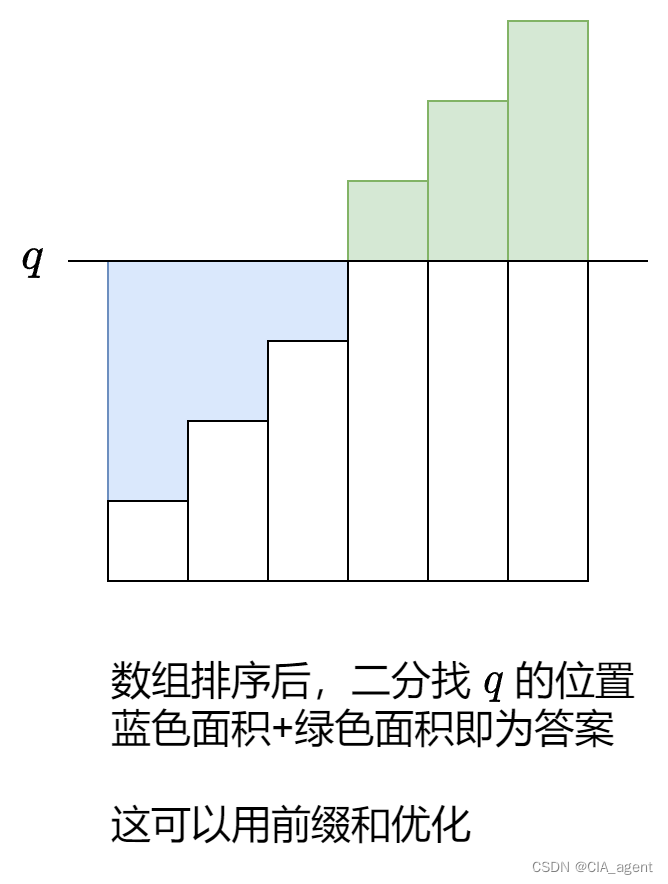
思路：可以用前缀和来减少计算， 如下图，先把 nums 从小到大排序，查找每个 query 在 nums 中的 index， index 左边的每个数都小于 query， index 右边的每个数都大于 query, 则 左边和就是 index*query - curSum[index]， 右边也同理，这样代码就很容易写出来了。

class Solution:
    ### return index(最小为 -1), 其中 index 左边的 <= target, index 右边的都比 target 大
    def findIndex(self, nums, target):
        l, r = 0, len(nums)-1
        while l < r:
            mid = int((l+r)/2)
            if nums[mid] <= target:
                if nums[mid+1] > target:
                    return mid
                else:
                    l = mid+1
            else:   # nums[mid] > target
                r = mid - 1
        if nums[l] > target:
            return -1
        return l

    def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:
        nums = sorted(nums)
        curSum = [0 for i in range(len(nums)+1)]
        curSum[0] = 0   ## 最前面塞一个值便于后续边界条件处理
        curSum[1] = nums[0]
        ### curSum[i] 表示 nums 前 i个数之和
        for i in range(2, len(nums)+1):
            curSum[i] = curSum[i-1] + nums[i-1]
        res = []
        for x in queries:
            index = self.findIndex(nums, x)+1  ## +1 用于 curSum 查找
            leftSum = x*index - curSum[index]
            rightSum = curSum[-1] - curSum[index] - x*(len(nums)-index)
            res.append(leftSum + rightSum)
        return res