一、堆排序思想

int a[] = { 2,3,5,7,4,6 };

对于这样一个数组来说，要想要用堆排序对它进行排序，首先要做的就是用数组里的数据建立一个堆，大堆和小堆都可以，只有是一个堆才能使用堆排序。

那么应该建大堆还是小堆呢，例如对于这个数组要排升序，如果建立小堆的话
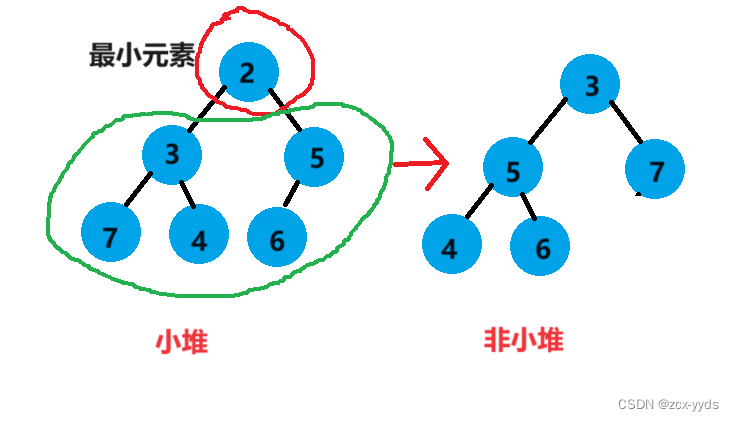
在这里插入图片描述

建成小堆后找出了最小的元素，要找到次小的就需要把剩下的元素看作堆，但剩下的元素不一定是堆，需要重新建堆，代价比较大。

更好的方法是升序建立大堆，堆顶和最后一个元素交换，最后一个最大的元素就已经有序，对剩下数据进行向下调整，就能找出第二大的，以此就能将数组排好序。

总结一下堆排序的思想就是：
1、根据要排什么序建大堆或小堆，此时堆顶端的元素就是最值
2、将顶端元素和末尾元素交换，此时末尾元素就是有序的，剩下的还有n-1个元素
3、将剩下的n-1个元素再次构建成堆，然后将堆顶端元素与第n-1个元素互换，反复执行便可得到有序数组

升序：建大堆
降序：建小堆

二、向上调整建堆排序

使用向上调整算法建堆的堆排序

例如：将数组a用堆排序按从小到大排列（升序）

在这里插入图片描述
首先，利用向上调整算法建大堆，此方法可参考堆的创建

向上调整算法的前提条件是：前面的元素是堆

对于单个结点来说既可以看作一个大堆，所以便可以通过向上调整算法依次对数组元素进行调整，那进行调整的元素前就一定是堆，满足条件

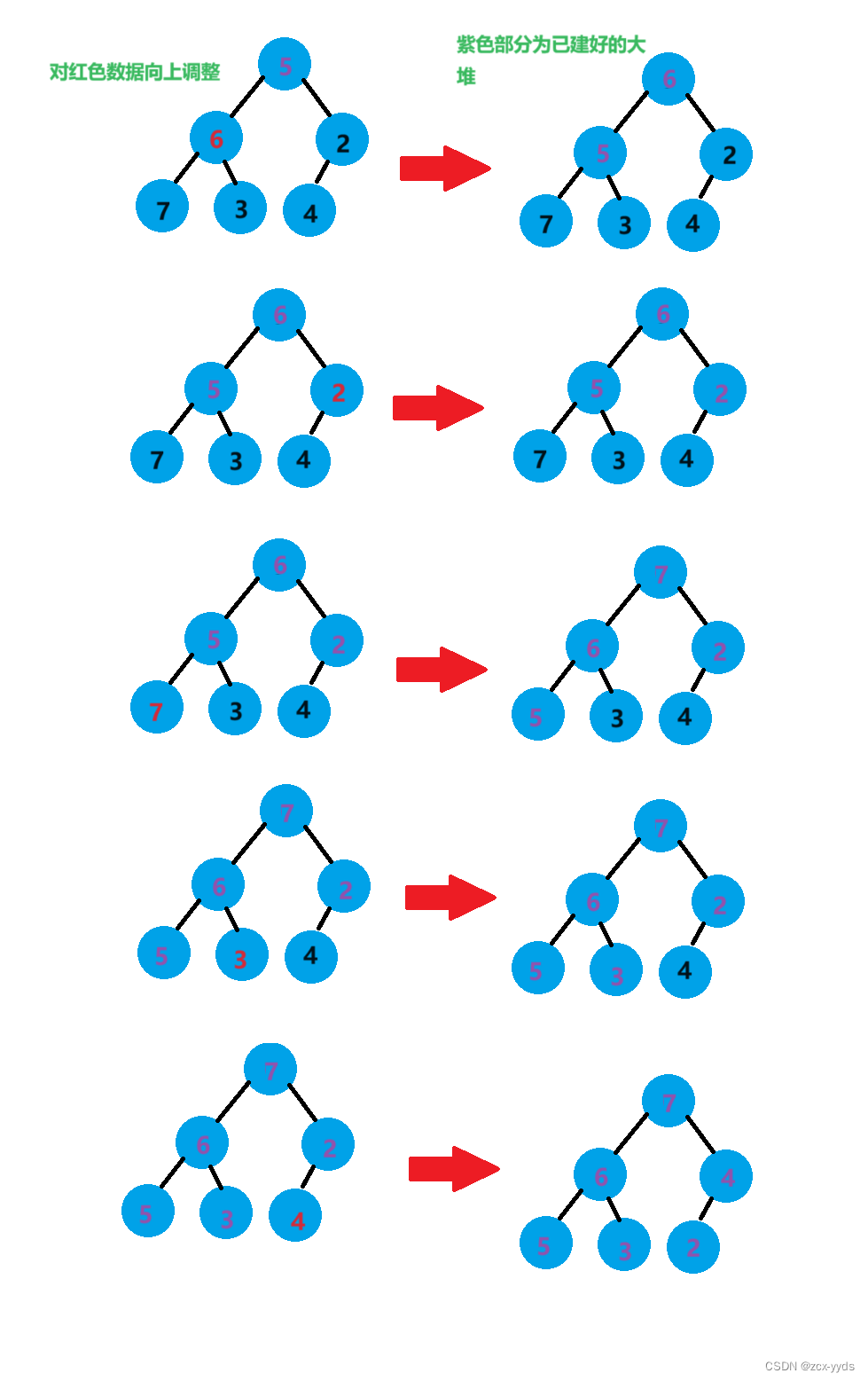
在这里插入图片描述

创建好的大堆如下：
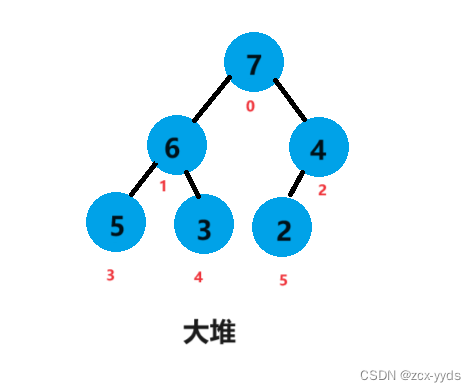
在这里插入图片描述

将堆的顶端元素7和末尾元素2进行交换，对除7外剩下的元素进行向下调整重新构建大堆
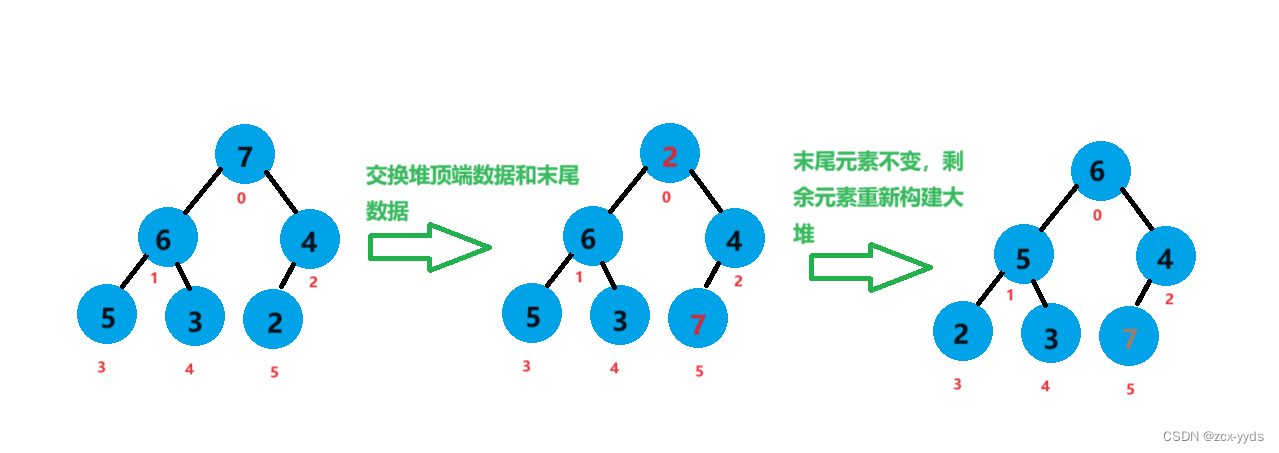
在这里插入图片描述
此时7已经是有序的，将元素6和元素3进行交换，对除6、7外剩下元素进行向下调整重新构建大堆

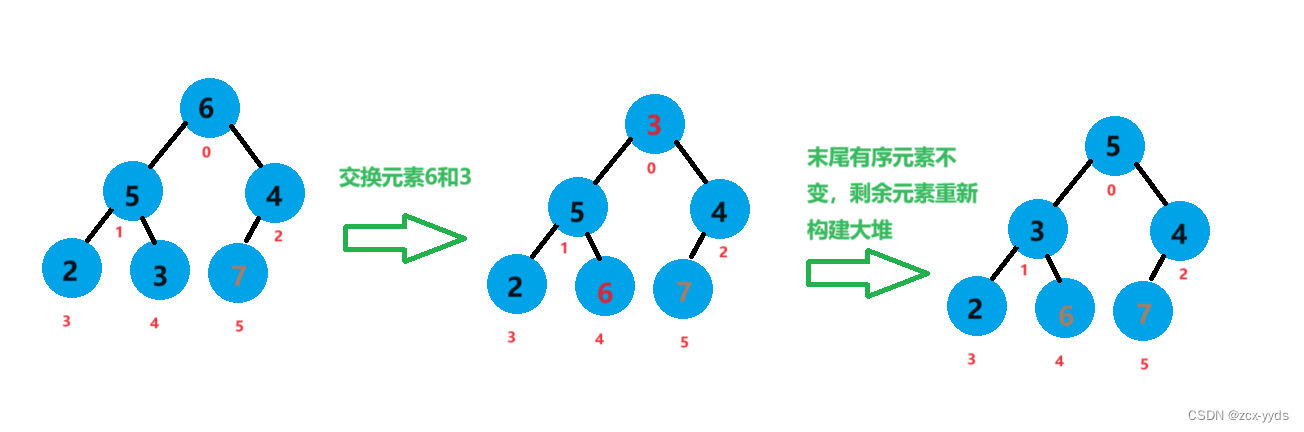
此时6、7已经有序，将元素5和元素2进行交换，对除5、6、7外剩下元素进行向下调整重新构建大堆

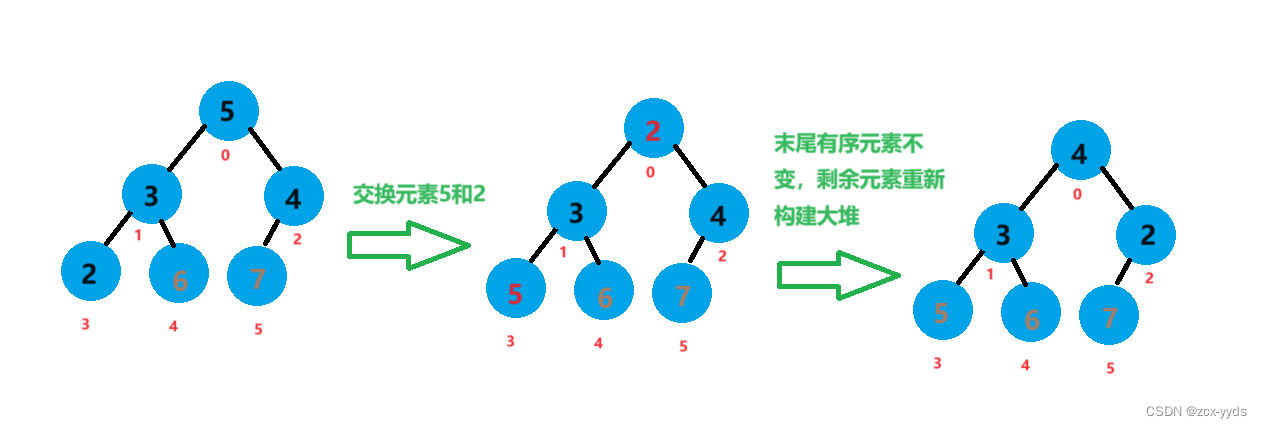
此时5、6、7已经有序，将元素4和元素2进行交换，此时数组已经有序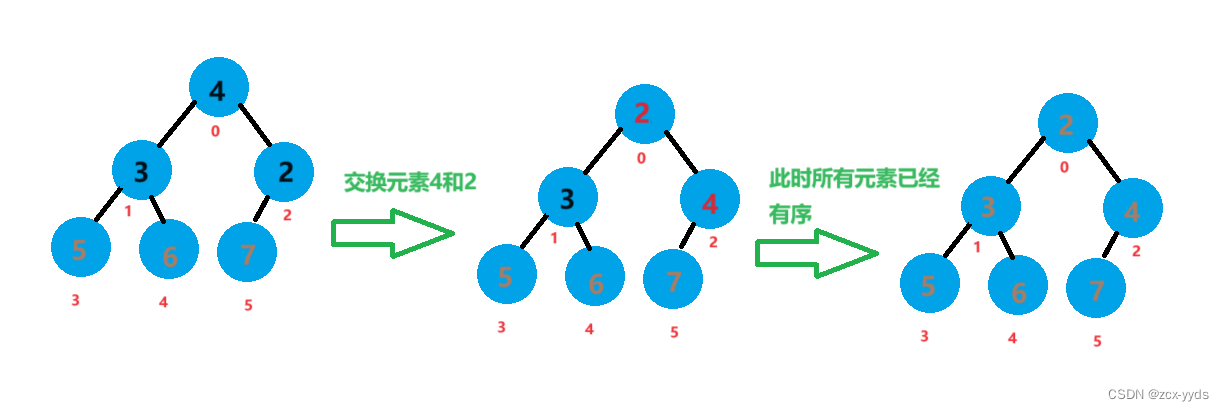在这里插入图片描述
排序完数组a变为

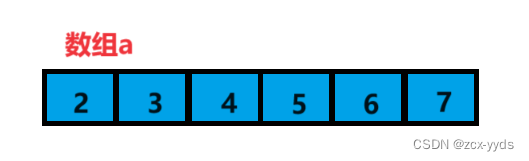
用向上调整算法建堆的升序的堆排序代码如下：

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int HPDataType;
//交换结点的函数
void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
//向上调整算法(大堆)
void AdjustUp(HPDataType* a, int child)
{
	//找出双亲的下标
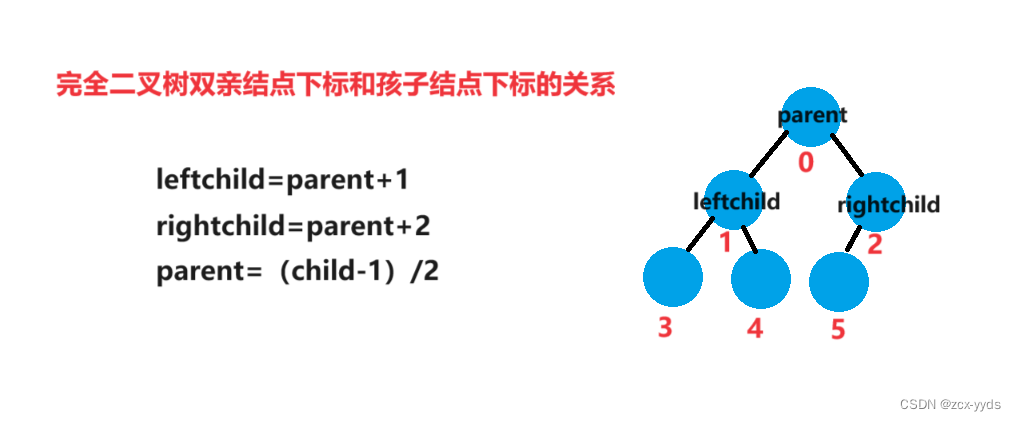
	int parent = (child - 1) / 2;

	while (child>0)
	{
		//孩子结点比双亲大则交换
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

//向下调整算法(大堆)
void AdjustDown(HPDataType* a, int n, int parent)
{
	//先默认左孩子是较大的
	int child = parent * 2 + 1;

	while (child < n)
	{
		//找出左右孩子中较大的
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		//孩子节点更小则交换
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//排序
void HeapSort(int* a, int n)
{
	//向上调整建堆
	for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}
	//最尾端数据下标为总数减一
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		//对剩余元素进行向下调整
		AdjustDown(a, end, 0);
		end--;
	}
}
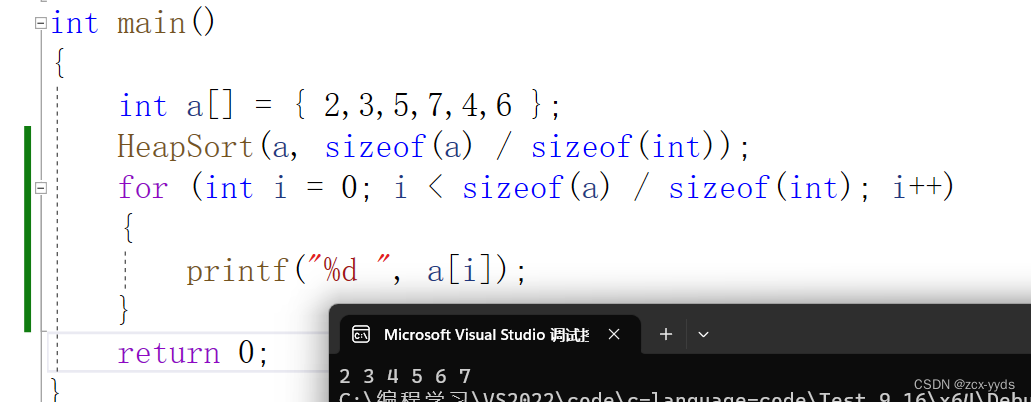
int main()
{
	int a[] = { 2,3,5,7,4,6 };
	HeapSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

运行结果如下：
在这里插入图片描述

空间复杂度：O(1)
平均时间复杂度：O(nlogn)

三、向下调整建堆排序

向下调整建堆排序与向上调整建堆排序不同的地方就在于建堆时用的算法不同，建好堆之后的后续操作都是相同的。

还是对上面那个案例，我们用向下调整算法建堆
在这里插入图片描述

向下调整算法前提条件：左右子树必须是堆，才能调整

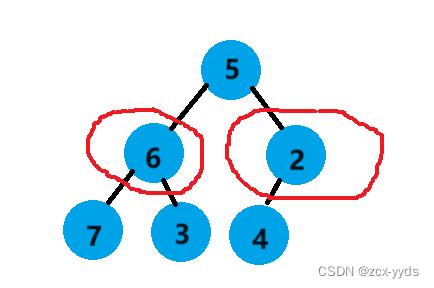
在这里插入图片描述

对于这个完全二叉树来说，它的倒数第一个非叶子节点2的左子树为4，没有右子树，可以用向下调整，再上一个节点6的左右子树是单个节点也可以看作堆，所有我们就可以从倒数第一个非叶子节点也就是最后一个节点的父亲开始向下调整：

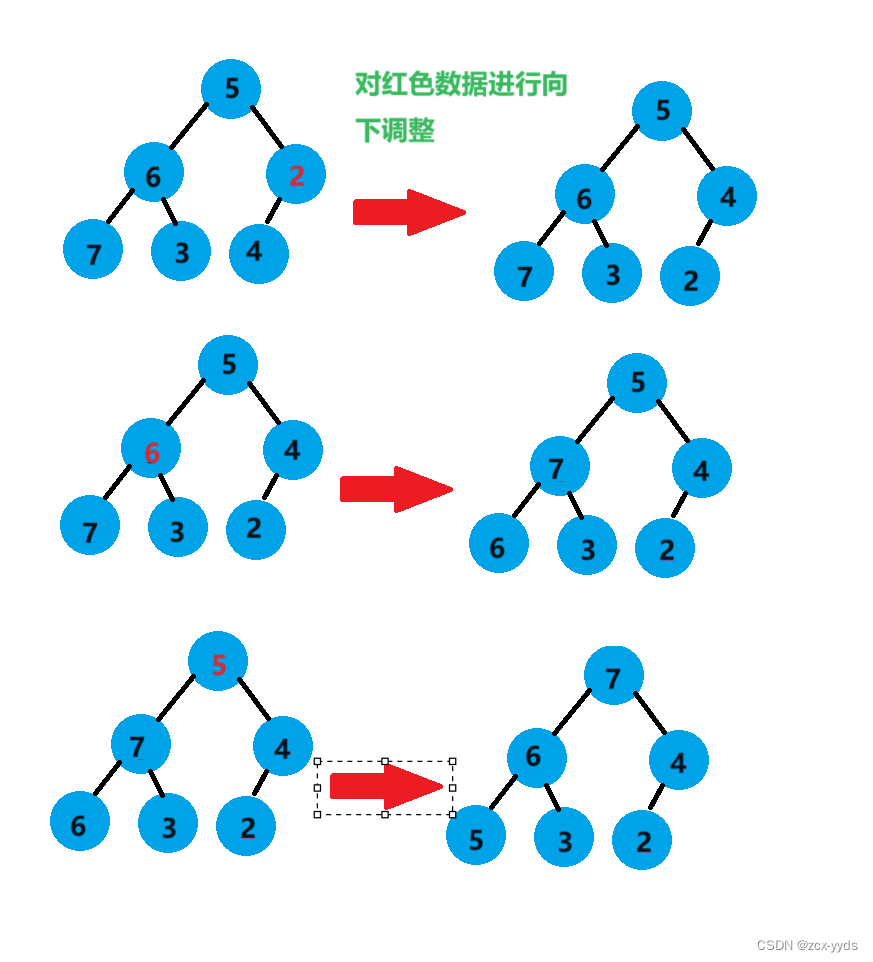
在这里插入图片描述

利用向下调整建好堆之后的后续操作与向上调整建好堆之后的操作一样，这里就不再演示

用向下调整算法建堆的升序的堆排序代码更改如下：

void HeapSort(int* a, int n)
{
	向上调整建堆
	//for (int i = 1; i < n; i++)
	//{
	//	AdjustUp(a, i);
	//}
	// 
	//向下调整建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	//最尾端数据下标为总数减一
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		//对剩余元素进行向下调整
		AdjustDown(a, end, 0);
		end--;
	}
}