1.三种常见的简单排序：

1.1冒泡排序

1.2 选择排序

1.3 插⼊排序

2 常见高级排序算法

2.1 希尔排序

2.2 快速排序

2.3 归并排序

2.4计数排序

先上结论：

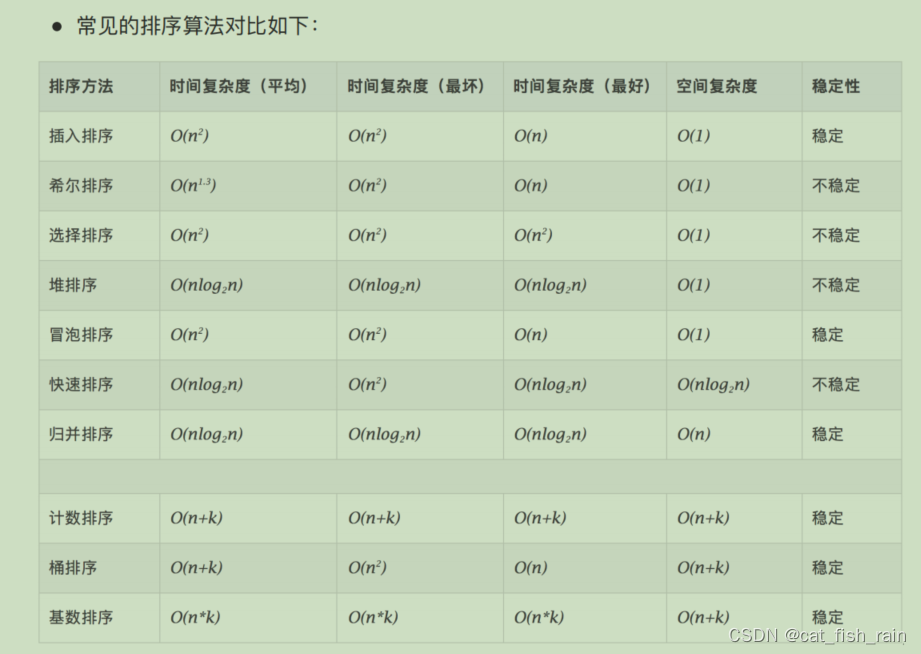
1.三种常见的简单排序：

1.1冒泡排序

1.⾸先在未排序数组的⾸位开始，和后⾯相邻的数字进⾏⽐较，如果前⾯⼀个⽐后⾯⼀个⼤

那么则进⾏交换。

2.接下来在将第⼆个位置的数字和后⾯相邻的数字进⾏⽐较，如果⼤那么则进⾏交换，直到将最⼤的数字交换的数组的尾部。

3.然后再从排序的数组的⾸位开始，重复前⾯两部将最⼤的数字交换到未排序数组的尾部（交换到尾部的数字是已经拍好序的）。如此反复，直到排序完毕。

代码。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

void bubbleSort(vector<int> &v)
{

    for (int i = 0; i < v.size() - 1; i++)
    {
        for (int j = 0; j < v.size() - i - 1; j++)
        {
            if (v[j] > v[j + 1])
            {
                swap(v[j], v[j + 1]);
            }
        }
    }
}

int main()
{

    vector<int> v = {10, 8, 2, 3, 1, 6, 7, 5, 4, 9};
    bubbleSort(v);

    for (auto i : v)
    {
        cout << i << endl;
    }

    system("pause");
    return 0;
}

1.2 选择排序

1⾸先在未排序序列中找到最⼩（⼤）元素，存放到排序序列的起始位置，

2.然后，再从剩余未排序元素中继续寻找最⼩（⼤）元素，然后放到已排序序列的末尾。

3.以此类推，直到所有元素均排序完毕。


void selectionSort(vector<int> &arr)
{
    int n = arr.size();
    int min_index; //最小值对应的index;

    for (int i = 0; i < arr.size(); i++)
    {
        min_index = i; //默认最小值对应的起始索引是当前位置
        for (int j = i; j < arr.size(); j++)
        {

            if (arr[j] < arr[min_index])
            {
                min_index = j;
            }
        }
        swap(arr[i], arr[min_index]);
    }
}

1.3 插⼊排序

1 从第⼀个元素开始，该元素可以认为已经被排序；

2 取出下⼀个元素，在已经排序的元素序列中从后向前扫描；

3 如果该元素（已排序）⼤于新元素，将该元素移到下⼀位置；

4 重复步骤 3 ，直到找到已排序的元素⼩于或者等于新元素的位置；

5 将新元素插⼊到该位置后；

6 重复步骤 2~5 。

// 插入排序函数
void insertionSort(vector<int> &arr)
{
    int n = arr.size();
    for (int i = 1; i < n; ++i)
    {
        int key = arr[i];
        int j = i - 1;

        // 将大于key的元素向后移动
        while (j >= 0 && arr[j] > key)
        {
            arr[j + 1] = arr[j];
            j = j - 1;
        }

        // 插入key到正确的位置
        arr[j + 1] = key;
    }
}

2 常见高级排序算法

2.1 希尔排序

2.1 算法描述

1959 年 Shell 发明，第⼀批突破 O(n2) 时间复杂度的排序算法，是简单插⼊排序的改进版。它与插⼊排序的不同之处在于，它会优先⽐较距离较远的元素。希尔排序⼜叫缩⼩增 量排序

算法核⼼思想是先将整个待排序的记录序列分割成为若⼲⼦序列分别进⾏直接 插⼊排序 ，具体算法描述：

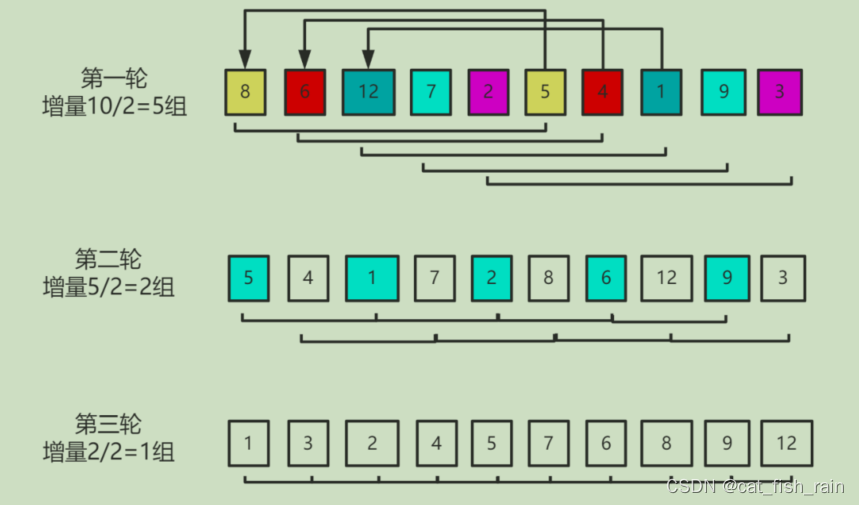
1.先根据数组的⻓度 /n ，获取增量 K （第⼀次 n 为 2 ）

2.按增量序列个数 k 进⾏分组，⼀般可以分成 k 组；

3.根据以分好的组进⾏插⼊排序；（每组排序，根据对应的增量 k 来找到当前组的元素）

4.当每组都排序完毕之后，回到第⼀步将 n*2 再次分组进⾏插⼊排序，直到最终 k=1 的时候，在执⾏⼀次插⼊排序 完成最终的排序

void shellSort(vector<int> &arr)
{
    int n = arr.size();

    // 使用一组增量进行排序
    for (int gap = n / 2; gap > 0; gap /= 2)
    {
        // 对每个增量进行插入排序
        for (int i = gap; i < n; i++)
        {
            int temp = arr[i];
            int j;

            // 将元素插入到正确的位置
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
            {
                arr[j] = arr[j - gap];
            }

            arr[j] = temp;
        }
    }
}

2.2 快速排序

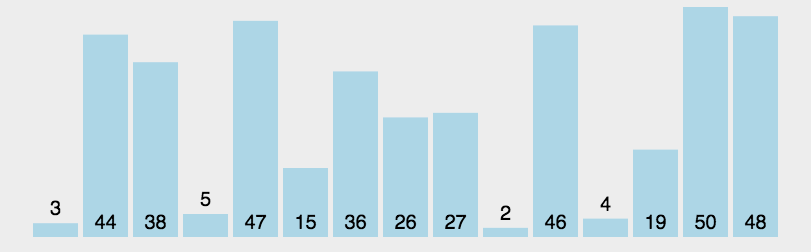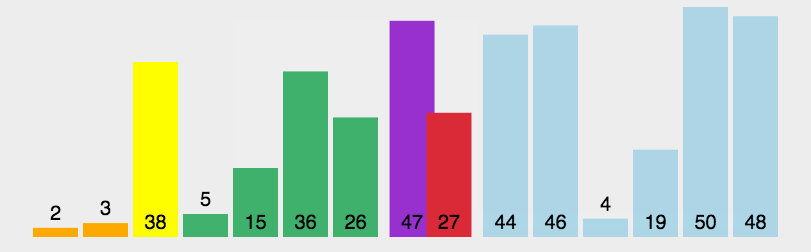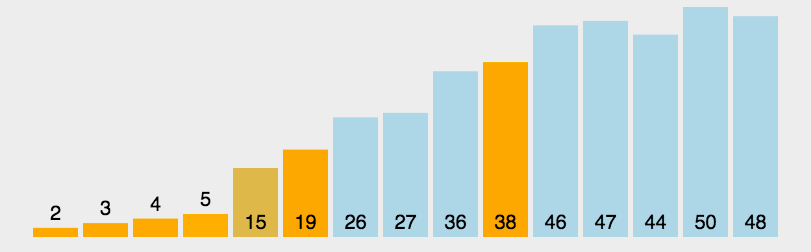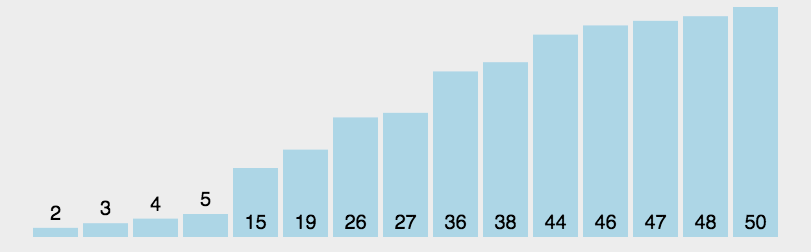
快速排序是对冒泡排序的⼀种改进，通过分⽽治之的思想减少排序中交换和遍历的次数，整个过程可以通过递归的⽅式完成。

具体描述如下 :

1 ，⾸先通过⽐较算法 , 找到基准数，⽐较过程通过交换，最终达到基准数左边的数字都⽐较右边的要⼩。分⽐在头尾设置两个指针，并且再将尾部元素作为⽐较基准。

移动 L 和 R 两个指针，直到重合，然后交换基准数字

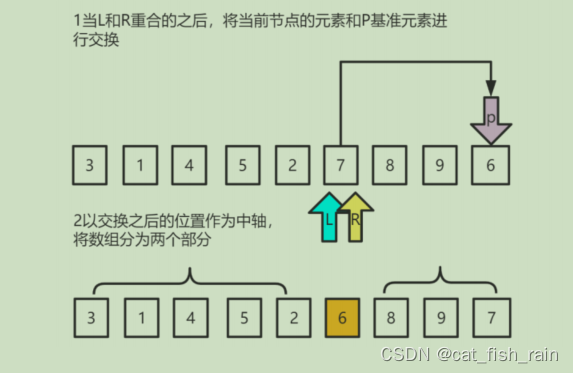
2 ，然后以基准数作为中轴，将数组分为两部分，分⽐执⾏ 1 步骤的算法（可以通过递

归实现），直到⽆法再次分割排序完毕。

递归

⼀个含直接或间接调⽤本函数语句的函数被称之为递归函数，它必须满⾜以下两个条件：

1 ）在每⼀次调⽤⾃⼰时，必须是（在某种意义上）更接近于解；

2 ）必须有⼀个终⽌处理或计算的准则。

算法实现

分解 1 ：创建左右两个指针，将最后⼀个值作为基准值，通过不断交换将数组分为两部

分，左边的⽐右边的要⼩。

先判断左指针和基准的值，如果⼩于等于就向后移动，直到遇到⽐基准值⼤的值

再判断右边指针和基准值，如果⼤于等于就向前移动，直到遇到⽐基准值⼩的值

然后交换左右指针的值。

循环上述操作，直到左右指针重合，然后交换重合值和基准值


// 根据基准元素将数组分成两部分，并返回基准元素的索引
int partition(vector<int> &arr, int low, int high)
{
    int pivot = arr[high]; // 选择最后一个元素作为基准
    int i = (low - 1);     // 初始化较小元素的索引

    for (int j = low; j <= high - 1; j++)
    {
        // 如果当前元素小于或等于基准元素，则交换arr[i+1]和arr[j]
        if (arr[j] <= pivot)
        {
            i++;
            swap(arr[i], arr[j]);
        }
    }

    // 最后交换arr[i+1]和arr[high]，将基准元素放在正确的位置
    swap(arr[i + 1], arr[high]);
    return (i + 1);
}

// 快速排序主函数
void quickSort(vector<int> &arr, int low, int high)
{
    if (low < high)
    {
        // 获取基准元素的索引
        int pivotIndex = partition(arr, low, high);

        // 对基准元素的左边和右边子数组进行递归排序
        quickSort(arr, low, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, high);
    }
}

int main()
{

    vector<int> v = {10, 8, 2, 3, 1, 6, 7, 5, 4, 9};
    // bubbleSort(v);

    // selectionSort(v);
    // insertionSort(v);
    // shellSort(v);
    quickSort(v, 0, v.size() - 1);

    for (auto i : v)
    {
        cout << i << endl;
    }

    system("pause");
    return 0;
}

2.3 归并排序

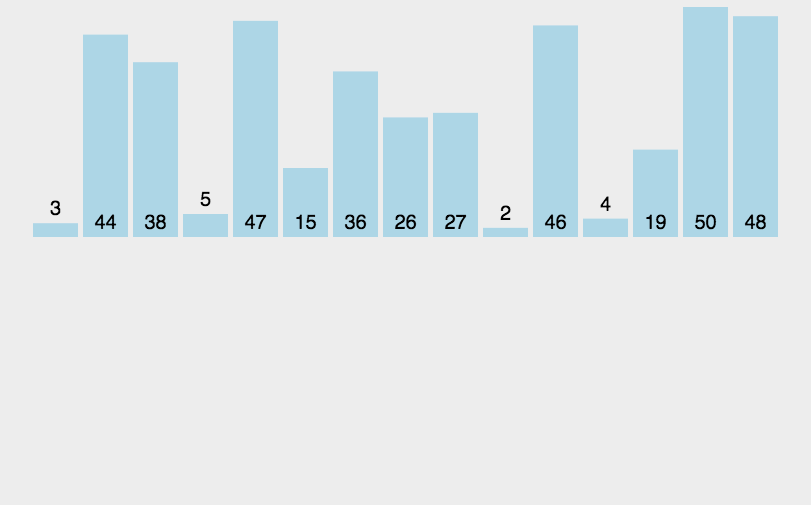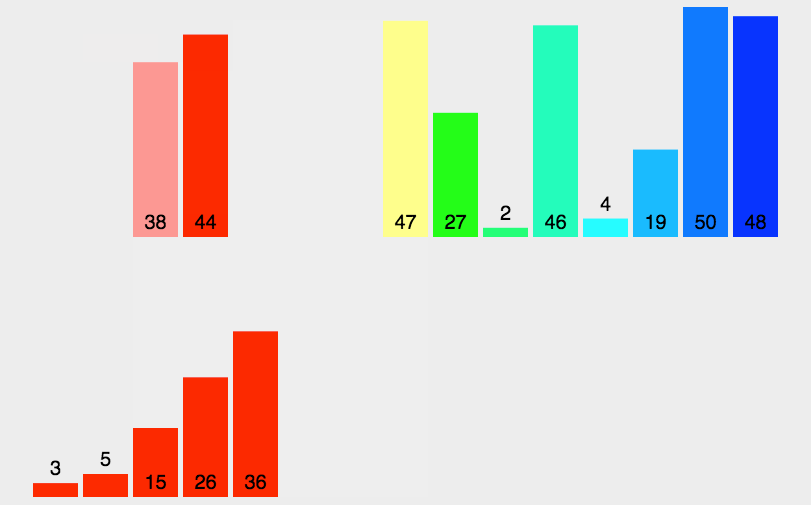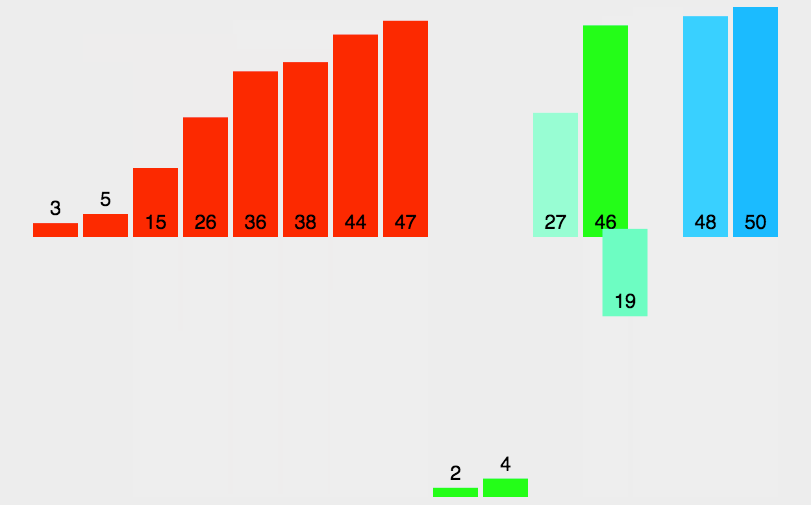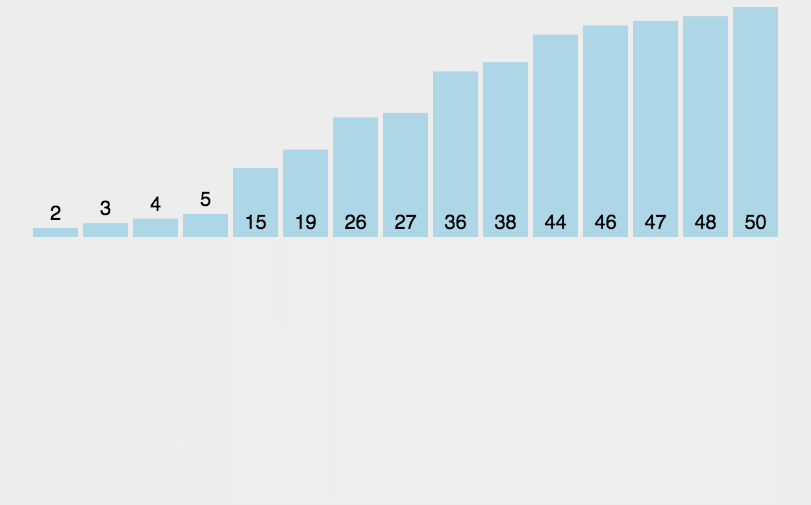
1.归并排序是利⽤归并的思想实现的排序⽅法，该算法采⽤经典的分治策略即将问题分成⼀

些⼩的问题然后递归求解，⽽治的阶段则将分的阶段得到的各答案 " 修补 " 在⼀起，即分⽽

治之

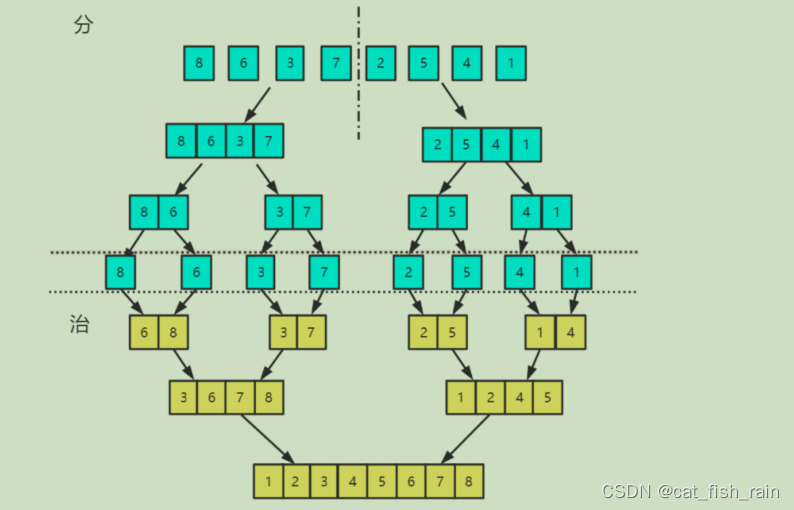
归并排序是稳定排序，它也是⼀种⼗分⾼效的排序，能利⽤完全⼆叉树特性的排序⼀般性

能都不会太差。 java 中 Arrays.sort() 采⽤了⼀种名为 TimSort 的排序算法，就是归并排序

的优化版本。从上⽂的图中可看出，每次合并操作的平均时间复杂度为 O(n) ，⽽完全⼆叉

树的深度为 |log2n| 。总的平均时间复杂度为 O(nlogn) 。⽽且，归并排序的最好，最坏，

平均时间复杂度均为 O(nlogn) 。

归并排序核⼼思想是先分再治 , 具体算法描述如下 :

1.先将未排序数组 /2 进⾏分组 , 然后再将分好组的数组继续 /2 再次分组 , 直到⽆法分组 , 这

个就是分的过程 .

2.然后在将之后再把两个数组⼤⼩为 1 的合并成⼀个⼤⼩为 2 的，再把两个⼤⼩为 2 的合

并成 4 的 , 同时在合并的过程中完成数组的排序 , 最终直到全部⼩的数组合并起来 , 这个

就是治的过程 .

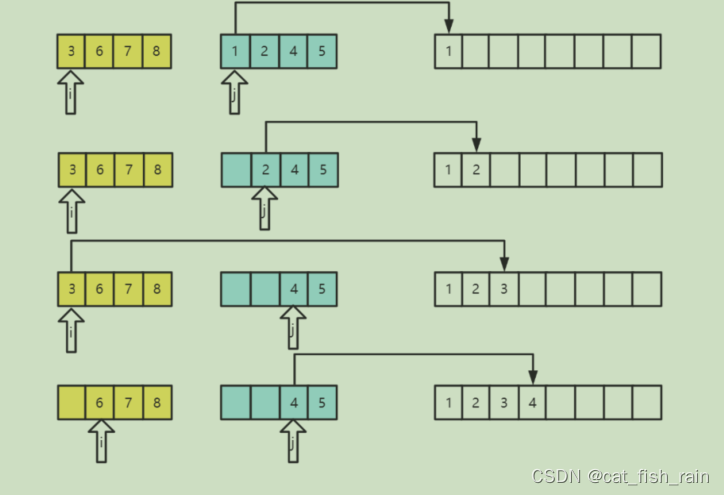
治的过程中会为两个数组设计两个游标 , 和⼀个新的数组 .

分⽐⽐较两个游标指对应数组的元素, 将⼩的插⼊到新的数组中

然后向后移动较⼩的数组的游标, 继续进⾏⽐较 .

反复前⾯两步, 最终将两个数组中的元素排序合并到新的数组中

#include <iostream>
#include <vector>

// 合并两个已排序的子数组
void merge(std::vector<int>& arr, int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;

    // 创建临时数组来存储两个子数组
    std::vector<int> leftArr(n1);
    std::vector<int> rightArr(n2);

    // 将数据复制到临时数组中
    for (int i = 0; i < n1; i++) {
        leftArr[i] = arr[left + i];
    }
    for (int i = 0; i < n2; i++) {
        rightArr[i] = arr[mid + 1 + i];
    }

    // 合并两个子数组
    int i = 0, j = 0, k = left;
    while (i < n1 && j < n2) {
        if (leftArr[i] <= rightArr[j]) {
            arr[k] = leftArr[i];
            i++;
        } else {
            arr[k] = rightArr[j];
            j++;
        }
        k++;
    }

    // 处理剩余的元素（如果有）
    while (i < n1) {
        arr[k] = leftArr[i];
        i++;
        k++;
    }
    while (j < n2) {
        arr[k] = rightArr[j];
        j++;
        k++;
    }
}

// 归并排序函数
void mergeSort(std::vector<int>& arr, int left, int right) {
    if (left < right) {
        // 找到数组中间点
        int mid = left + (right - left) / 2;

        // 递归排序左半部分和右半部分
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);

        // 合并已排序的两个子数组
        merge(arr, left, mid, right);
    }
}

int main() {
    std::vector<int> arr = {12, 11, 13, 5, 6, 7};

    std::cout << "原始数组: ";
    for (int num : arr) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    // 调用归并排序函数
    mergeSort(arr, 0, arr.size() - 1);

    std::cout << "排序后数组: ";
    for (int num : arr) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    return 0;
}

2.4计数排序

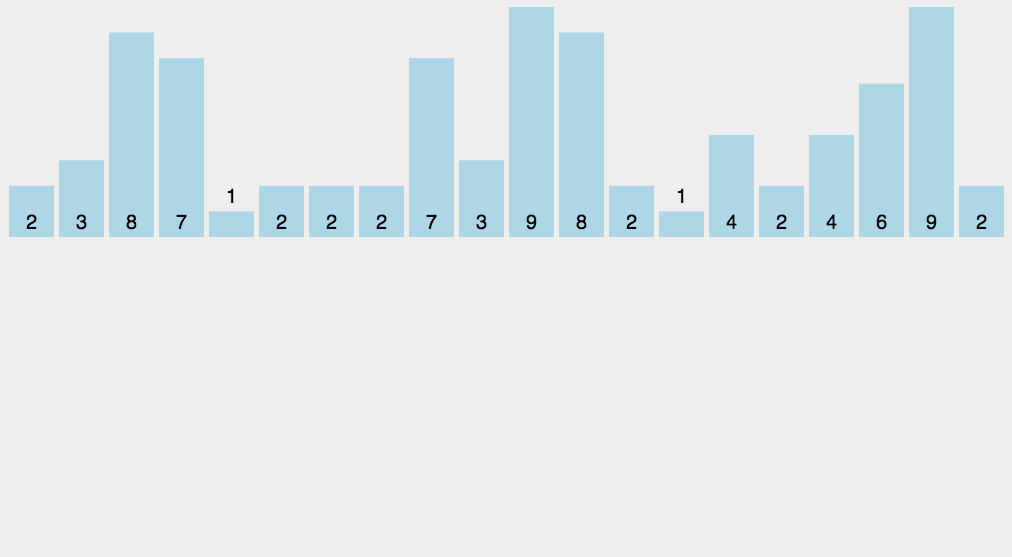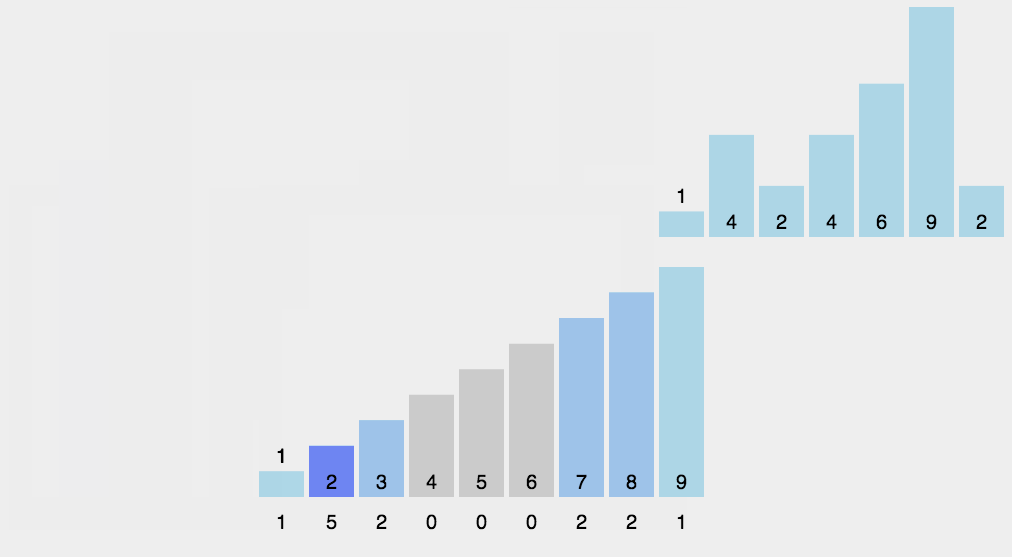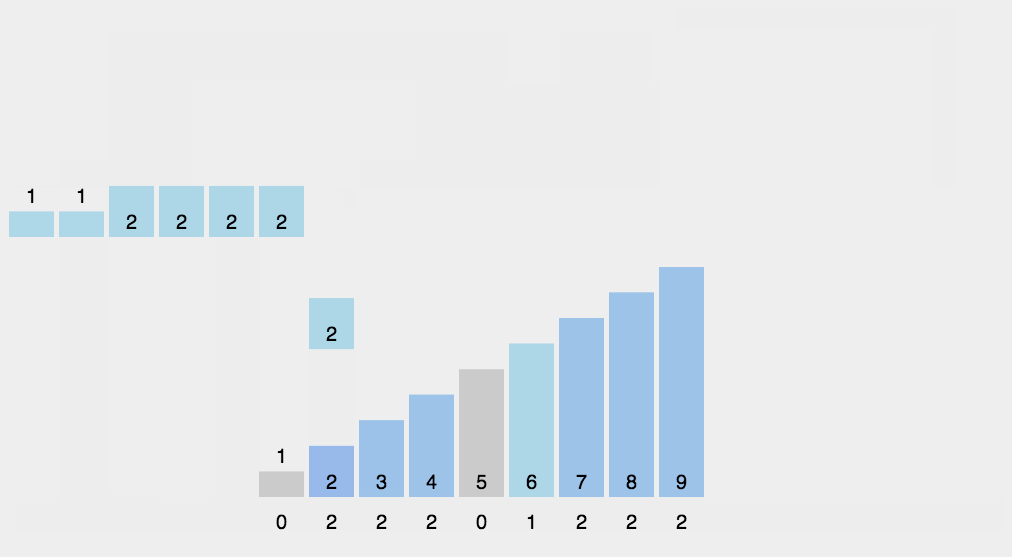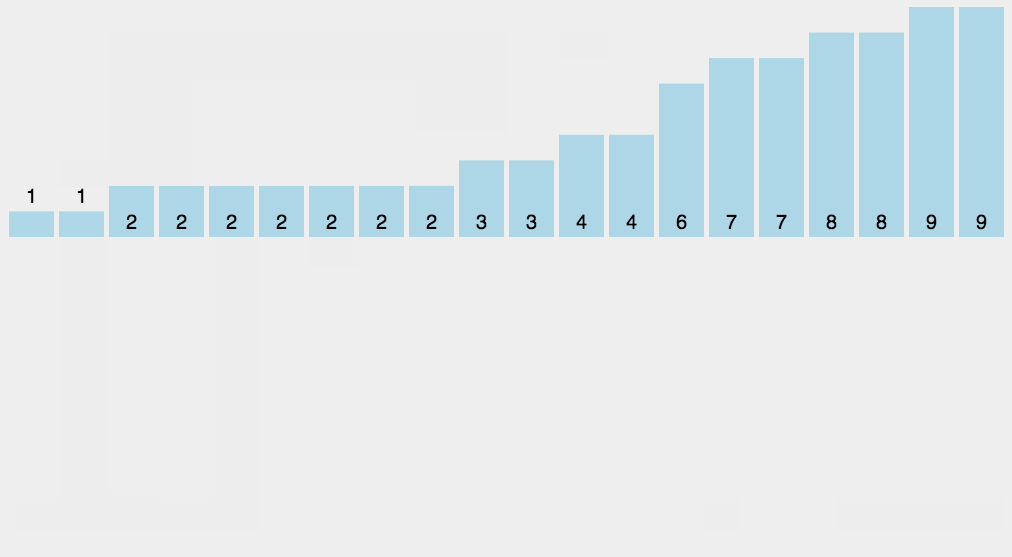
计数排序是⼀个⾮基于⽐较的排序算法，该算法于 1954 年由 Harold H. Seward 提出。它的优势在于在对⼀定范围内的整数排序时，它的复杂度为Ο (n+k) （其中 k 是整数的范围），快于任何⽐较排序算法。当然这是⼀种牺牲空间换取时间的做法，⽽且当 O(k)>O(nlog(n))的时候其效率反⽽不如基于⽐较的排序（基于⽐较的排序的时间复杂度在理论上的下限是O(nlog(n)), 如归并排序，堆排序）计数排序是⼀种适合于最⼤值和最⼩值的差值不是不是很⼤的排序，也就是说重复的数据

会⽐较多的情况。具体实现过程如下：⾸先遍历整个数组，找到最⼤的数字。

然后根据最⼤的数字创建⼀个临时统计数组，⽤于统计每个数字出现的次数，例如temp[i] = m, 表示元素 i ⼀共出现了 m 次。最后再把临时数组统计的数据从⼩到⼤返回到原来的数组中，这样就是有序的。

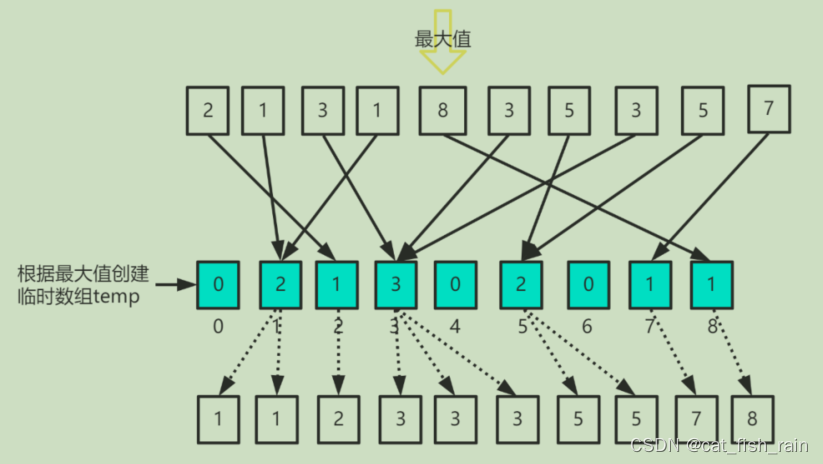
实现：

#include <iostream>
#include <vector>

void countingSort(std::vector<int>& arr) {
    int max_val = *std::max_element(arr.begin(), arr.end()); // 找到数组中的最大值
    int min_val = *std::min_element(arr.begin(), arr.end()); // 找到数组中的最小值

    int range = max_val - min_val + 1; // 计算数值范围

    // 创建计数数组并初始化为0
    std::vector<int> count(range, 0);

    // 计算每个元素的出现次数
    for (int num : arr) {
        count[num - min_val]++;
    }

    // 根据计数数组，重建原始数组
    int index = 0;
    for (int i = 0; i < range; i++) {
        while (count[i] > 0) {
            arr[index] = i + min_val;
            index++;
            count[i]--;
        }
    }
}

int main() {
    std::vector<int> arr = {4, 2, 2, 8, 3, 3, 1};

    std::cout << "原始数组: ";
    for (int num : arr) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    // 调用计数排序函数
    countingSort(arr);

    std::cout << "排序后数组: ";
    for (int num : arr) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    return 0;
}