概念

通过映射关系将关键字映射到存储位置，并实现增删改查操作。

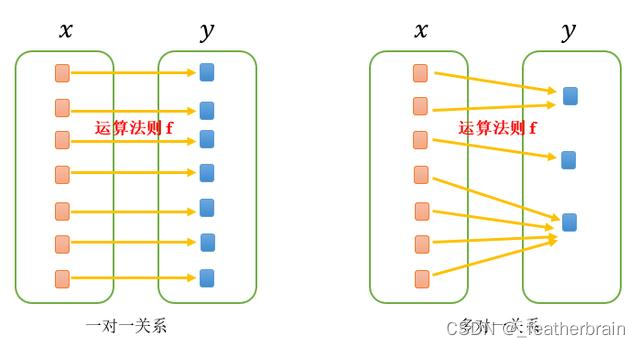
在这里插入图片描述

通过上面的方法构造出来的结构就叫哈希表（散列表），其中的映射关系叫做哈希函数

哈希冲突及原因

不同的关键字映射到同一个位置称为哈希冲突

原因：

哈希函数设计得不够合理

哈希函数设计原则：

哈希函数的定义域包括所有关键码，散列表的空间位 n，其值域为 $[0, m - 1]$
计算出来的地址均匀分布在整个散列表中
比较简单

其他类型哈希：

哈希函数需要将关键码进行取模操作，这就表示了当其他类型哈希时需要先将关键字转换为整型 —— 可以通过仿函数进行转换。

解决哈希冲突的方法

解决哈希冲突两种常见的方法是：闭散列和开散列

闭散列

闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。

寻找“下一个”空位置的方法：线性探测和二次探测

线性探测

从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。

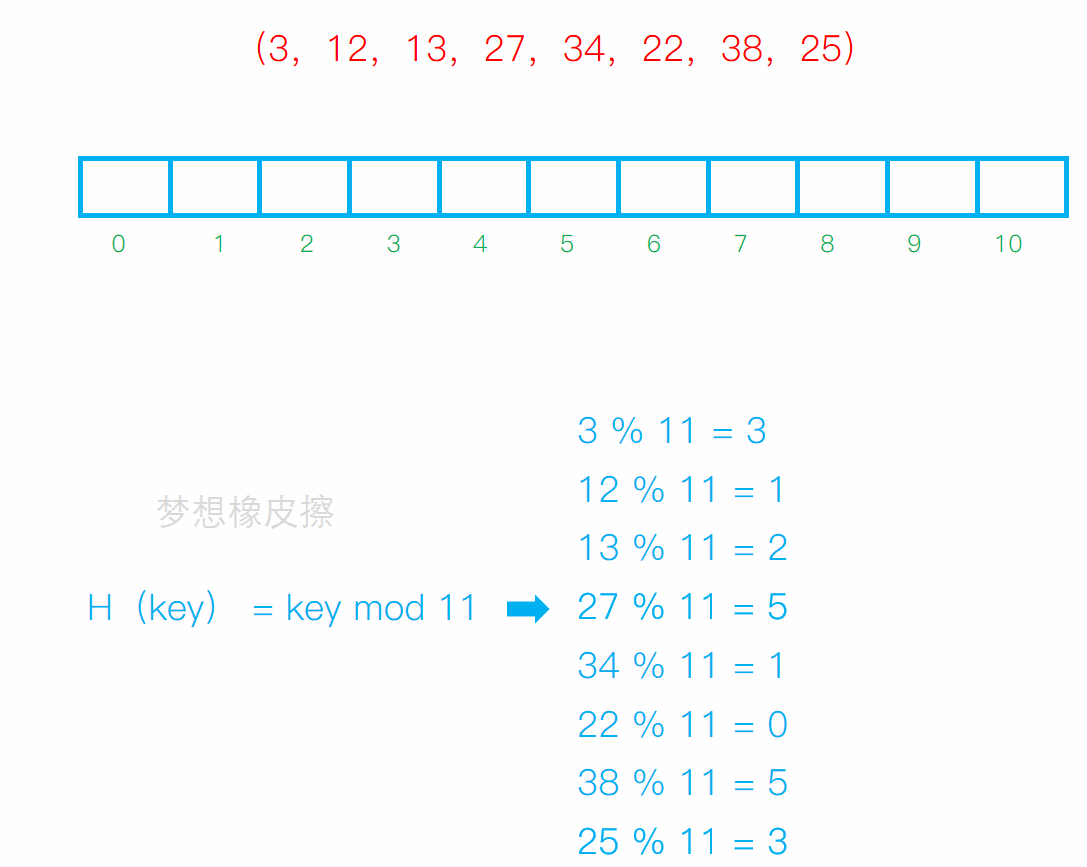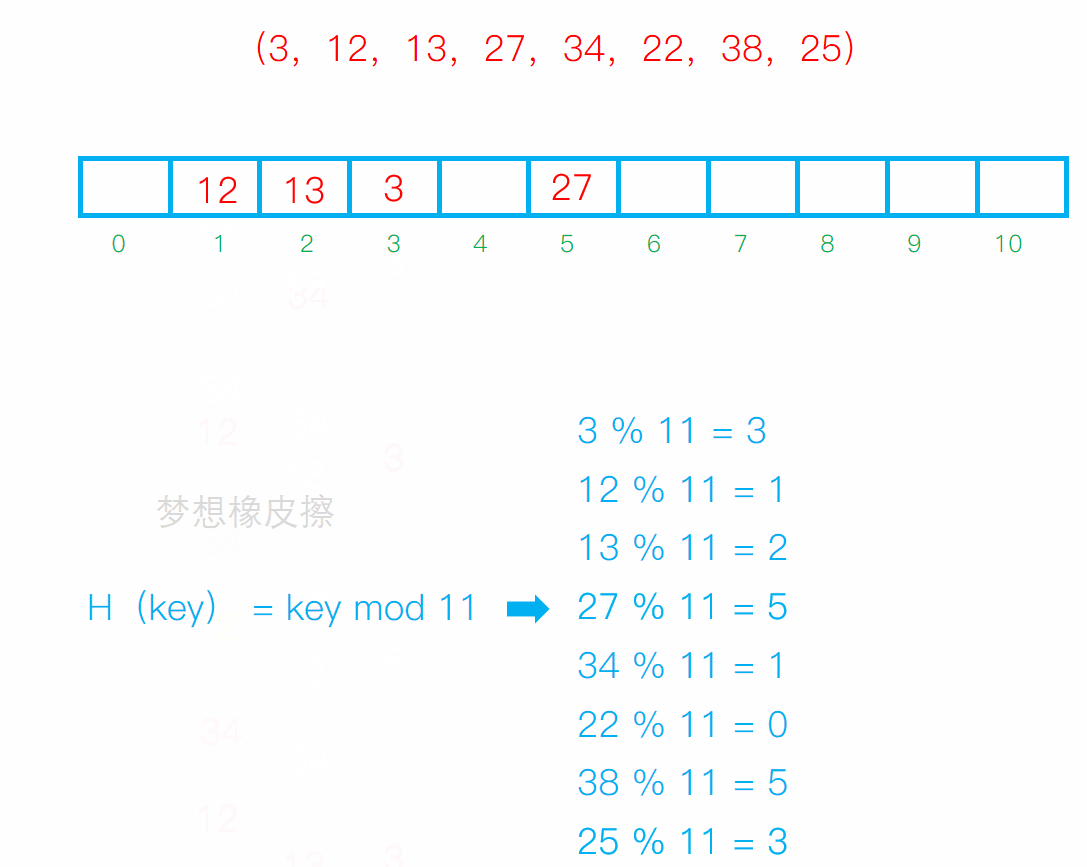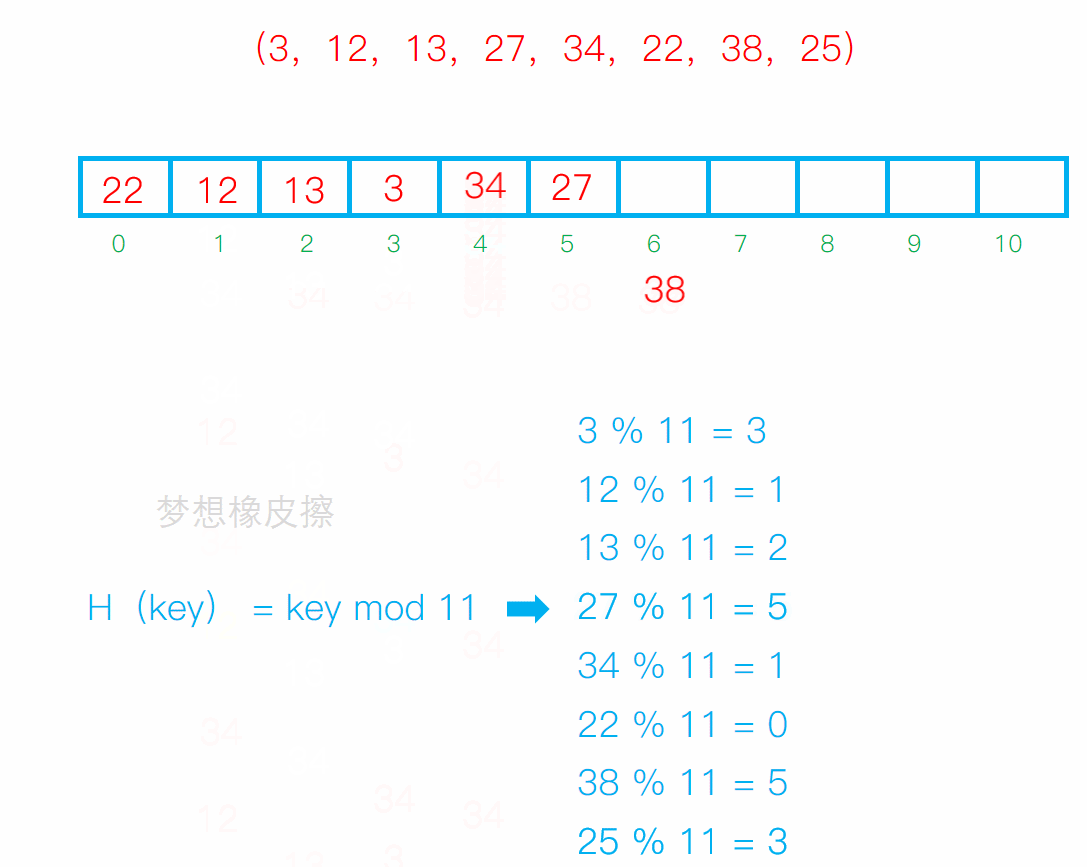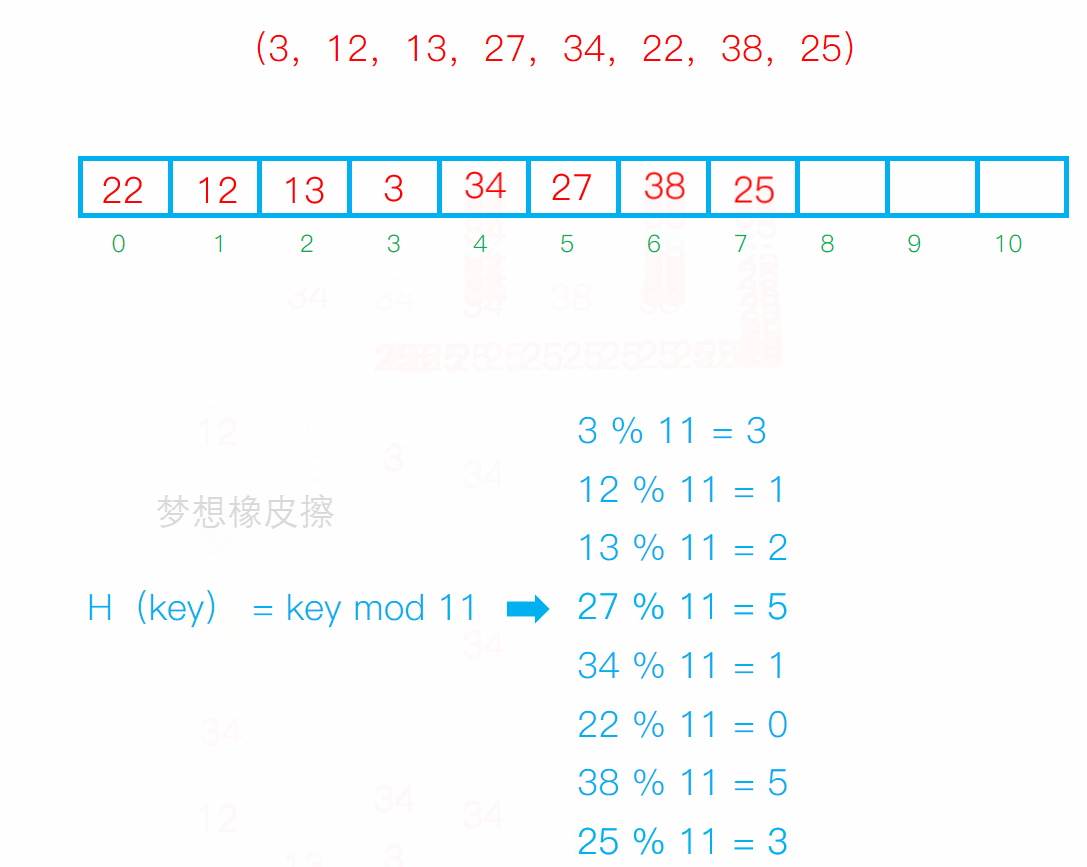
在这里插入图片描述

缺点：

冲突连在一起容易发生数据堆积，不同的关键字占用了可利用的空位置，使得同一个效率下降，影响效率

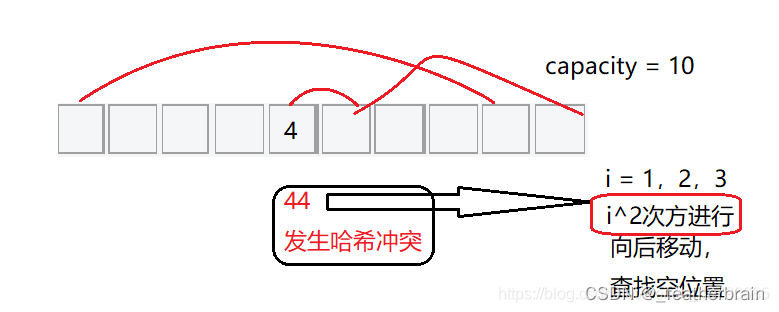
二次探测

线性探测造成数据堆积的原因是寻找空位置的方式，为了避免数据堆积，二次探测寻找下一个位置的方式为：

： $H_i = (H_0 + i^2 ) \% m$ , 或者： $H_i = (H_0 - i^2 ) \% m$ 。其中： $i = 1, 2, 3 \dots$ ， $H_0$ 是通过散列函数 $H a s h (x)$ 对元素的关键码 $k ey$ 进行计算得到的位置， $m$ 是表的大小。

在这里插入图片描述

扩容

当哈希表的载荷因子达到一定大是进行扩容

在这里插入图片描述

开散列

开散列法又叫链地址法(开链法)，将相同地址的关键字分为一个集合称为桶，通过单链表将桶中的元素链接起来。

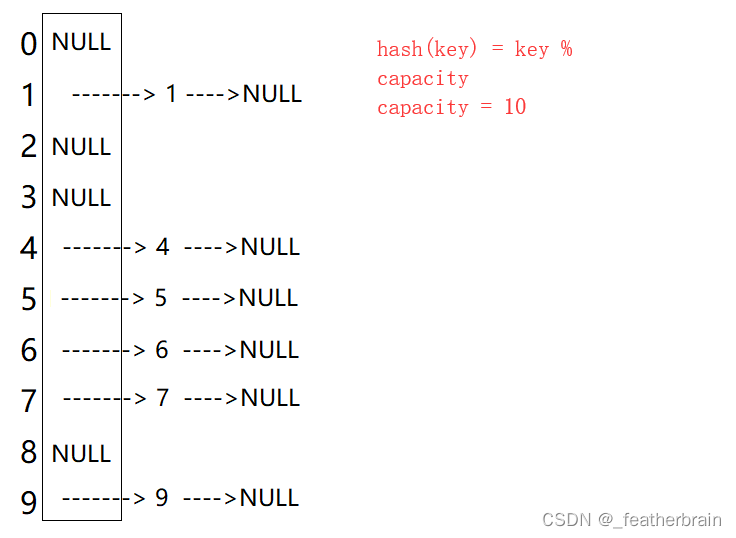
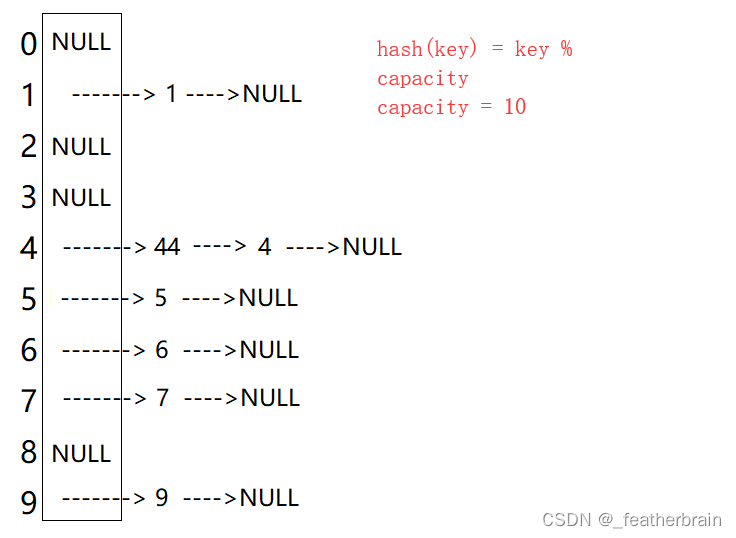
在这里插入图片描述

扩容

随着插入的增加，冲突的可能性越来越大即一个桶中节点越来越多，影响哈希表的性能。开散列最好的情况是每个哈希桶都只有一个节点，所以当 $元素个数 == 桶的个数$ 时进行扩容较为合理

哈希的应用

位图

用一个比特位来存放某种状态，用来快速判断某个数据在不在。

模拟实现：

template<size_t N = 100>
class bitset
{
public:
	bitset(size_t n = N)
	{
		_bit.resize(N / 8 + 1, 0);
	}

	bitset& set(size_t x, bool val = true)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		
		if (val)
		{
			_bit[i] |= 1 << j;
		}
		else
		{
			_bit[i] &= ~(1 << j);
		}

		return *this;
	}

	bitset& set()
	{
		vector<char> tmp(N / 8 + 1, 1);
		_bit.swap(tmp);
		return *this;
	}

	bitset& reset()
	{
		vector<char> tmp(N / 8 + 1, 0);
		_bit.swap(tmp);
		return *this;
	}

	bitset& reset(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;

		_bit[i] &= ~(1 << j);

		return *this;
	}

	bool test(size_t x) const
	{
		size_t i = x / 8;
		size_t j = x % 8;

		return _bit[i] & (1 << j);
	}

private:
	vector<char> _bit;
	size_t _size;
};