Python量化金融风险分析：一文全面掌握VaR计算

金融市场是一个复杂且多变的生态圈，涉及从经济数据到政治动态的各种影响因素。无论你身处何种角色——小投资者、企业财务，还是大型金融机构的资产经理，你都必须面对各种不确定性，例如股价波动、利率变动或突发事件如政治危机和自然灾害。

因此，量化风险评估不仅是一种科学需求，更是一种财务安全的基本保障。其中，Value at Risk（VaR）是一个广受欢迎的风险量化工具，能在特定置信水平和时间范围内，预测资产组合可能面临的最大潜在损失。

VaR不仅在资产管理和资本配置方面有广泛应用，也被用于评估市场风险、信贷风险和流动性风险。而计算VaR的方法也多种多样，从历史模拟法到蒙特卡洛模拟法，各有利弊。本文将详细介绍VaR的主要计算方法，并演示如何使用Python来实现这些方法，让你能更全面地掌握金融风险量化的核心技术。

VaR的计算方法

VaR是一个用于度量金融资产组合在一定置信水平和预定时间内潜在最大损失的度量指标。用数学语言来说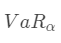，是随机变量 X（投资组合的收益或损失）的下分位数，即：

VaR 试图回答这样一个问题：在给定的置信水平（如95%或99%）和时间范围（如一天、一周、一个月等）内，资产组合可能面临的最大潜在损失是多少？如一个投资组合的一日99% VaR为100万元，这意味着在99%的情况下，该组合在一天内不会损失超过100万元。然而，这并不意味着该组合就绝对安全，因为还有1%的概率会造成超过100万元的损失。

====================================================================================================================================================================================

0****1

方差-协方差法

在方差-协方差法中，我们通常假设资产收益服从正态分布，且市场波动性和资产收益的相关性在短期内稳定。对于正态分布，其概率密度函数（pdf）和累积分布函数（cdf）有良好的数学性质。

对于标准正态分布，累积分布函数 F(x) 给出了随机变量 X 小于或等于 x 的概率。例如，F(0)=0.5 表示标准正态分布下随机变量小于或等于 0 的概率是 50%。VaR 通常表示为一个资产或投资组合在给定置信水平（通常为 95% 或 99%）和给定时间期限T 内可能会面临的最大预期损失。假设资产收益 R 服从均值为和标准差为的正态分布，则置信水平下的 VaR 可以表示为：

其中：是标准正态分布在置信水平下的 Z 分数。例如，对于 95% 的置信水平，通常取 1.645 或 1.65。是资产或投资组合的日度或年度波动性（标准差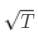）。是用于调整时间期限的因子。如果是日波动性，而 T 是以日为单位，则。

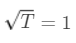这个公式的推导基础是正态分布的数学性质。在正态分布中，和能够完全描述分布的形状。通过正态分布的逆累积分布函数（即分位数函数），我们可以找到在置信水平下对应的 Z 分数（）。这个 VaR 公式非常直观且计算简单，但它依赖于正态分布假设，这一假设在现实金融市场中并不总是成立。因此，在使用方差-协方差法时，必须谨慎处理其局限性。

下面使用Python获取数据并使用方差-协方差法计算创业板指数的日收益率VaR值，代码如下：

import numpy as np  
import pandas as pd  
import qstock as qs  
import matplotlib.pyplot as plt  
from scipy.stats import norm  
import seaborn as sns

#获取数据  
df=qs.get_data('cyb',start='20130101',end='20230913')  
returns=df.close.pct_change().dropna()  
qs.hist_kde(returns)

# 计算标准差  
std_dev = returns.std()  
  
# 置信水平为 95%  
confidence_level = 0.95  
  
# 查找相应的Z分数  
z_score = norm.ppf(confidence_level)  
  
# 时间窗口（以天为单位）  
time_period = 5  # 一周有5个交易日  
  
# 计算一周的VaR  
VaR1= -z_score * std_dev * np.sqrt(time_period)  
  
print(f"在95%的置信水平下，一周的价值在险（VaR）为：{VaR1:.4f}")

在95%的置信水平下，一周的价值在险（VaR）为：-0.0703

在95%的置信水平下，一周的价值在险（VaR）为0.0703意味着，在所有可能的市场走势中，有95%的概率你在持有创业板指数的一周内最多会面临7.03%的资本损失。这是在假设模型和市场条件稳定的前提下的风险预测。

def plot_var(var):  
    plt.figure(figsize=(10,5))  
    sns.histplot(data=returns,kde=True, stat='count')  
    plt.text(var, 100, f'VAR：{round(var, 4)}',   
          horizontalalignment='right',  
          size=12,   
          color='navy')  
    rect=plt.Rectangle((var,0),-0.06,250,color = 'mistyrose')  
    plt.gca().add_patch(rect)  
    plt.show()

plot_var(VaR1)

0****2

历史模拟法

历史模拟法是一种简单直观的VaR计算方法，不需要对收益率的分布做任何假设。该方法直接使用过去的历史数据来估计未来的风险。步骤如下：

收集历史数据: 从历史价格或收益率数据中进行抽样。
排序数据: 将历史收益率数据从最小到最大进行排序。
选择置信水平: 如置信水平是95%，则查找对应于最低的5%收益率的值。

在历史模拟法中，我们通常使用单日的收益率进行分析。然而，如果你想计算一个更长时间段（如一周）的VaR，有两个选择：（1）直接使用单日收益率来计算VaR，并假设这些收益率在你关心的时间段内（一周）是独立且相同分布的。这样你可以通过合适的数学方法（比如，乘以如果你假设收益率是正态分布的）来扩展到一周。但这样做有一个明显的缺点，即它不考虑可能存在的时间相关性和收益率分布的偏态等特点。（2）直接计算每一周的累积收益率，并在这个基础上进行VaR计算。这样做的好处是它能够更准确地反映多日内资产价值的变动，因为它考虑了多天收益率的复合效应。计算一周的累积收益率是为了更准确地捕捉一周内可能出现的收益率波动，这对于某些市场（特别是波动性很高或有明显时间序列相关性的市场）来说可能是更合适的。

下面使用第二种选择进行历史模拟法的计算，代码如下：

# 置信水平为 95%  
confidence_level = 0.95  
# 时间窗口（以天为单位）  
time_period = 5  # 一周有5个交易日  
# 计算一周的累积收益率  
cumulative_returns = (1 + returns).rolling(window=time_period).apply(np.prod) - 1  
# 计算在1 - 置信水平（这里是5%）处的分位数  
VaR2 = np.percentile(cumulative_returns.dropna(), 100 * (1 - confidence_level))  
print(f"在{confidence_level * 100}%的置信水平下，一周的价值在险（VaR）为：{VaR2:.4f}")

在95.0%的置信水平下，一周的价值在险（VaR）为：-0.0654

风险值-0.0654表示在 95% 的置信水平下，最大损失为 6.54%，或者损失超过 6.54% 的概率为 5%。可以这么理解，对于 100,000 的投资，我们有 95% 的把握最大损失为 6,540。

0****3

Bootstrap法

Bootstrap 方法类似于历史方法，但在这种情况下，我们对回报进行多次采样，如 100 次或 1000 次或更多次，计算 VaR，最后取平均 VaR。这类似于在数据科学空间中进行的重采样，其中数据集被多次重采样，模型被重新训练以预测值。

def calculate_bootstrap_VaR(returns, confidence_level=0.95,   
                            iterations=1000, time_period=5):  
    """  
    使用Bootstrap法计算VaR  
    参数:  
        returns (pd.Series or np.array): 收益率序列  
        confidence_level (float): 置信水平，取值范围在0到1之间  
        iterations (int): Bootstrap迭代次数  
        time_period (int): 考虑的时间周期（例如：5天表示一周）  
    返回:  
        VaR(float): 在给定置信水平下一周的VaR值  
    """  
    bootstrap_VaRs = []  # 存储Bootstrap VaR的结果  
  
    # 开始Bootstrap迭代  
    for i in range(iterations):  
        # 有放回地随机抽取样本  
        sample = np.random.choice(returns, size=time_period, replace=True)  
        # 计算一周的累积收益率  
        cumulative_return = np.prod(1 + sample) - 1  
        bootstrap_VaRs.append(cumulative_return)  
    # 计算VaR  
    bootstrap_VaRs = np.sort(bootstrap_VaRs)  
    VaR= np.percentile(bootstrap_VaRs, 100 * (1 - confidence_level))  
    return VaR  
  
VaR3 = calculate_bootstrap_VaR(returns)  
print(f"使用Bootstrap法，95%的置信水平的五日价值在险（VaR）为：{VaR3:.4f}")

使用Bootstrap法，95%的置信水平的五日价值在险（VaR）为：-0.0642

0****4

蒙特卡洛模拟

蒙特卡洛模拟是一种通过模拟随机过程来估计某个变量的分布的方法。因此，蒙特卡洛方法通常涉及到根据某种概率模型生成数据，然后用这些生成的数据来估计分布。在VaR的计算中，这通常涉及假设资产收益率遵循某种分布（如正态分布），然后从该分布中随机抽样。

def simulate_values(returns, iterations=1000,n = 5,p=0.05):  
    mu=returns.mean()  
    sigma= returns.std()  
    try:  
        result = []        
        for i in range(iterations):  
            # 时间窗口（以天为单位）  
            # 计算一周的累积收益率  
            tmp_val = pd.Series(np.random.normal(mu, sigma, (len(returns))))   
            cum_ret = (1 + tmp_val).rolling(n  
                                ).apply(np.prod, raw=True) - 1  
            # 计算在1 - 置信水平（这里是5%）处的分位数  
            var = np.percentile(cum_ret.dropna(), p*100)  
            result.append(var)  
        return np.mean(result)  
    except Exception as e:  
        print(e)  
  
VaR4 = simulate_values(returns)  
print(f"使用蒙特卡洛模拟法，95%置信水平五日价值在险（VaR）为：{VaR4:.4f}")

使用蒙特卡洛模拟法，95%置信水平五日价值在险（VaR）为：-0.0661

值得注意的是，这个模型是基于日收益率服从正态分布的假设的，这一假设在实际应用中可能并不准确。因此，在使用这个模型时应谨慎，并可能需要对其进行进一步的检验和调整。

0****5

衰减因子法

衰减因子法（也被称为指数加权移动平均模型，EWMA）是一个金融时间序列模型，经常用于金融风险管理中。相较于简单的历史模拟法，它赋予近期的数据更高的权重，因此它可以更快地捕捉到市场的变动。

衰减因子的基本思想是近期的观测值比较重要，因此应当给予更高的权重。而较早之前的观测值逐渐“衰减”并被赋予较低的权重。公式如下：

其中，是时点 t 的波动率的估计，是时点 t-1 的收益率，是衰减因子（通常接近1，例如0.94或0.97）。一旦得到了波动率的估计，就可以使用正态分布假设来计算VaR。

def calculate_decay_factor_VaR(returns, lambda_factor=0.94,   
                    confidence_level=0.95, time_period=5):  
    """  
    使用衰减因子法计算VaR  
  
    参数:  
        returns (pd.Series or np.array): 收益率序列  
        lambda_factor (float): 衰减因子  
        confidence_level (float): 置信水平，取值范围在0到1之间  
        time_period (int): 考虑的时间周期（例如：5天表示一周）  
  
    返回:  
        VaR (float): 在给定置信水平下的VaR值  
    """  
    # 计算日波动率  
    variance = np.zeros_like(returns)  
    for t in range(1, len(returns)):  
        variance[t] = lambda_factor * variance[t-1] + \  
                   (1-lambda_factor) * returns[t-1]**2  
    volatility = np.sqrt(variance)  
  
    # 使用正态分布假设计算VaR  
    VaR = -norm.ppf(1-confidence_level) * volatility * np.sqrt(time_period)  
  
    return -VaR[-1]  # 返回最新的VaR值  
  
VaR5 = calculate_decay_factor_VaR(returns)  
print(f"使用衰减因子法，95%的置信水平一周VaR为：{VaR5:.4f}")

使用衰减因子法，95%的置信水平一周VaR为：-0.0416

注意，衰减因子法也是假设收益率是正态分布的，这可能不适用于所有金融资产。在实践中，金融资产的收益率可能会有厚尾或者偏度，需要更复杂的模型来处理。

0****6

GARCH模型

在金融风险管理中，广义自回归条件异方差（GARCH）模型用于捕捉金融时间序列波动性的复杂模型，与基础的EWMA模型相比，这些模型能更精确地捕捉金融资产收益率的动态特性。

GARCH模型使用了条件异方差的概念，可以用于预测波动率：

# 使用GARCH(1,1)模型  
from arch import arch_model  
#将收益率转为百分比  
garch_model = arch_model(returns*100, p=1, q=1)  
garch_fit = garch_model.fit(update_freq=5)  
forecast = garch_fit.forecast(start=0)  
  
# 获取最后一天的预测波动率  
final_volatility = np.sqrt(forecast.variance.values[-1,0])  
  
# 计算VaR  
VaR6 = norm.ppf(0.05) * final_volatility * np.sqrt(5)/100  # 5天，95%置信度  
print(f"使用GARCH方法，在95%的置信水平下，一周的价值在险（VaR）为：: {VaR6:.4f}")

`Iteration:      5,   Func. Count:     35,   Neg. LLF: 7267535.843682719   Iteration:     10,   Func. Count:     64,   Neg. LLF: 5102.880767591566   Optimization terminated successfully    (Exit mode 0)               Current function value: 5102.879334090473               Iterations: 14               Function evaluations: 83               Gradient evaluations: 14   使用GARCH方法，在95%的置信水平下，一周的价值在险（VaR）为：: -0.0464`

0****7

极值理论

极值理论（Extreme Value Theory, EVT）是一种统计学方法，专门用于研究随机变量分布的极端尾部行为。这一理论在金融、气象学、工程和其他多个领域有着广泛的应用，尤其在金融风险管理方面非常重要。在金融市场中，大多数分布的中心（即均值附近）的行为可以用常规的统计模型（如正态分布、对数正态分布等）进行描述，但这些模型往往不能准确捕捉分布尾部的极端事件。这些极端事件，虽然发生概率低，但一旦发生，其影响通常是巨大和灾难性的。

EVT 提供了一系列模型和方法，用于更准确地估计这些罕见但重要的极端事件。通过适当地建模和参数估计，EVT 可以用于计算价值在险（Value at Risk, VaR）、期望损失（Expected Shortfall）以及其他尾部风险度量。常用的 EVT 模型有广义极值分布（Generalized Extreme Value, GEV）和高阈值方法（Peaks Over Threshold, POT）。

from scipy.stats import genextreme as gev  
# 使用极端值分布（GEV）拟合数据尾部  
c, loc, scale = gev.fit(-returns[returns < np.percentile(returns, 5)])  
# 设置置信水平  
confidence_level = 0.95  
# 计算VaR  
VaR_1= -gev.ppf(confidence_level, c, loc, scale)  
print(f"在95%的置信水平下，一日在险价值（VaR）为：{VaR_1:.4f}")

在95%的置信水平下，一日在险价值（VaR）为：-0.0835

计算得到的一日VaR是0.0835，这意味着在95%的置信水平下，该资产一日内的最大预期损失不会超过8.35%。上述代码示例用于一日VaR的计算。对于多日VaR，你可以进行适当的缩放。

需要注意的是，这个简化方法是在一些假设下得到的，如金融资产收益率的独立性和相同分布等。如果这些假设不成立，那么这个简化公式的准确性就可能受到影响。

使用之前的代码片段，五日VaR的计算如下：

# 计算 5 日的 VaR  
VaR7 = VaR_1 * np.sqrt(5)  
print(f"在95置信水平下，资产五日价值在险（VaR）为：{VaR7:.4f}")

在95置信水平下，资产五日价值在险（VaR）为：-0.1867

var=[VaR1,VaR2,VaR3,VaR4,VaR5,VaR6,VaR7]  
index=['方差-协方差法','历史模拟法','Bootstrap法',  
 '蒙特卡洛模拟','衰减因子法','GARCH模型','极值理论']  
pd.Series(var,index=index).round(4)

方差-协方差法      -0.0703  
历史模拟法        -0.0654  
Bootstrap法   -0.0642  
蒙特卡洛模拟       -0.0661  
衰减因子法        -0.0416  
GARCH模型      -0.0464  
极值理论         -0.1867  
dtype: float64

计算金融资产在险价值（VaR）时，采用不同方法可能得到不同的 VaR 值。例如，在给出的数据中，方差-协方差法、历史模拟法、Bootstrap法和蒙特卡洛模拟产生的 VaR 值都在 -0.0642 到 -0.0703 的范围内，相对接近。这些方法通常用于描述一般的市场风险，并且每种方法都有其优缺点，如方差-协方差法的计算相对简单但依赖正态分布假设，而蒙特卡洛模拟更灵活但计算复杂。相对来说，衰减因子法（-0.0416）和 GARCH模型（-0.0464）给出了较低的 VaR 值，这可能反映了这些方法更多地考虑了近期的市场波动性。最引人注目的是，极值理论给出了明显更高的 VaR 值（-0.1867），这可能意味着该方法在预测罕见的市场极端事件方面具有更高的灵敏度。总体而言，每种方法都有其适用场景和局限性，选择哪一种取决于你的风险管理需求和对市场态势的判断。有时候，综合使用多种方法能够提供更全面和多角度的风险评估。

条件VaR（CVaR）

期望损失（Expected Shortfall, ES）也被称为条件VaR（Conditional VaR, CVaR）。与VaR只告诉我们在某个置信水平下可能面临的最大损失不同，ES（或CVaR）更进一步地衡量，当这种极端损失发生时，我们应预期多大的损失。

ES（CVaR）的计算公式是：

# 置信水平，例如95%  
alpha = 0.95  
  
# 首先计算VaR  
VaR = -np.percentile(returns, 100 * (1 - alpha))  
  
# 然后计算CVaR  
# 只考虑那些小于VaR（即更大损失）的收益率  
tail_losses = returns[returns < -VaR]  
CVaR = -tail_losses.mean()  
  
# 打印结果  
print(f"在95%的置信水平下，VaR（价值在险）为：{VaR:.4f}")  
print(f"在95%的置信水平下，CVaR（条件价值在险）或ES（期望损失）为：{CVaR:.4f}")

在95%的置信水平下，VaR（价值在险）为：0.0291  
在95%的置信水平下，CVaR（条件价值在险）或ES（期望损失）为：0.0464

VaR告诉我们，在给定的置信水平（这里是95%）下，预期的最大单日损失不会超过这个VaR值（如0.029）。CVaR或ES告诉我们，当损失超过VaR时，预期的平均损失将是CVaR（0.0464）。注意，这里使用历史模拟法来估计VaR和CVaR，这是一种非参数方法。在实际应用中，可能还需要考虑更多因素，如市场流动性、交易成本等。

结语

在险价值（Value-at-Risk, VaR）是一个广泛使用的风险管理工具，它提供了一种量化潜在损失的方法，并在置信水平和时间窗口内给出了最坏的预期损失。然而，VaR并不是万能的。虽然它能提供关于潜在损失的有用信息，但它也有局限性，如无法完全捕捉尾部风险，也不提供超出VaR水平后的损失大小。因此，在实践中，VaR通常与其他风险度量指标，如条件VaR（CVaR）或期望损失（ES）、CoVaR等，一同使用以获得更全面的风险评估。

使用VaR模型时，特别需要注意的是模型假设、数据质量和置信水平的选择，因为这些因素都会影响VaR的准确性和可靠性。同时，金融机构和个人投资者应当持续监控和调整其风险模型，以适应市场环境的变化。

---------------------------END---------------------------