本文不涉及:蒙特卡洛积分的原理以及渲染方程是如何推到出来，而是一步一步阐述蒙特卡洛路径追踪是如何解渲染方程的。

基本思想

渲染方程告诉我们的是，我们需要在物体表面的半球上进行积分，才能解出这个渲染方程，但是在半球上进行积分计算机不擅长做这个事情，因此我们采用蒙特卡洛积分解决这个问题

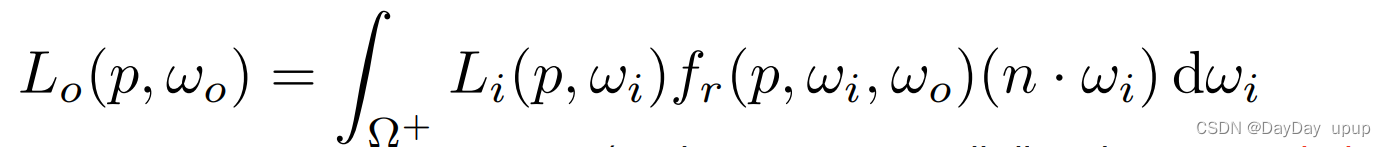
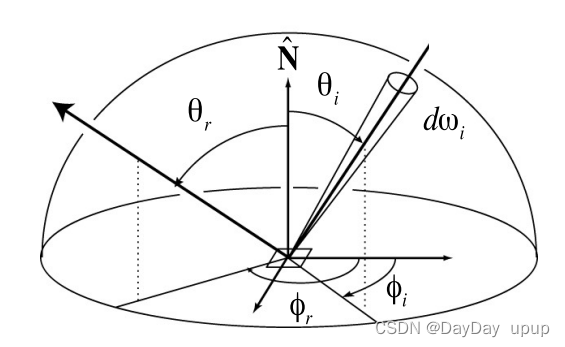
根据蒙特卡洛积分的原理，我们可以把连续的积分，转化成对离散的数值进行求和

基本代码

1. 从摄像机打出的光线直接打到了光源

2. 从摄像机打出的光线，打到了物体，光线经过弹射打到光源，根据蒙特卡洛积分，我们每次弹射都弹射N跟光线

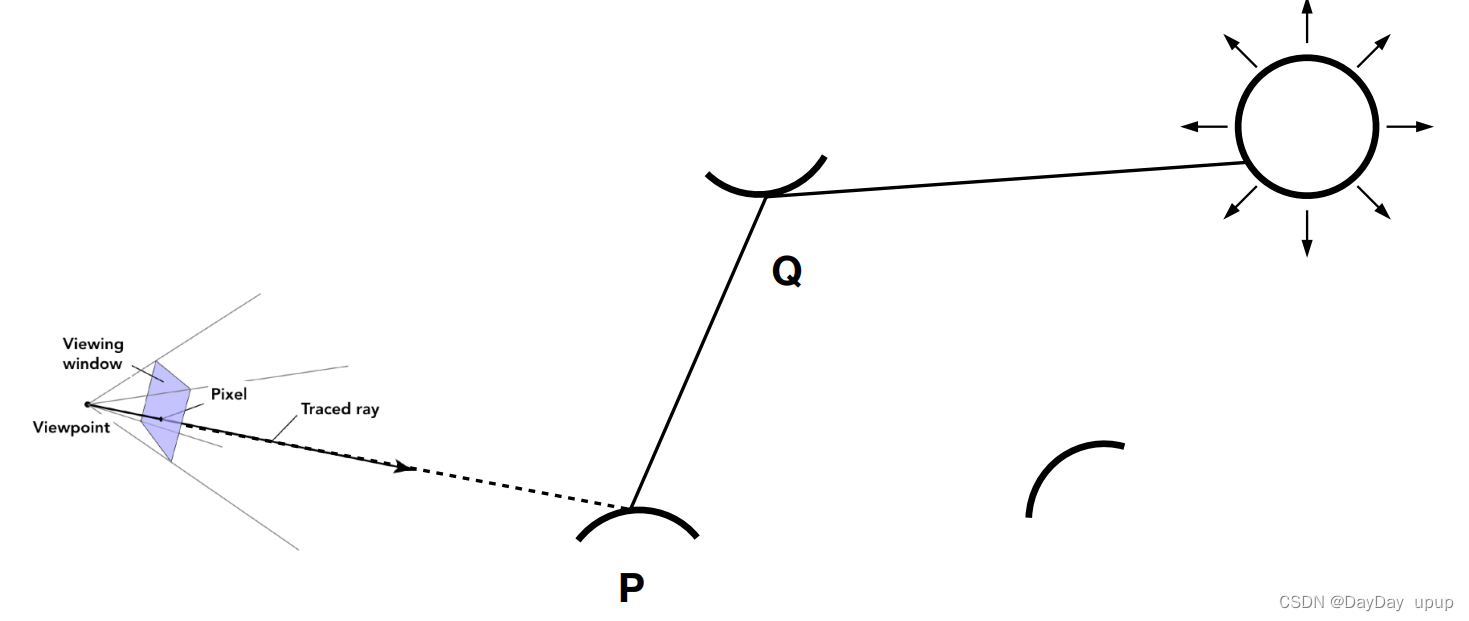
这样我们就得到了基本的代码

问题1:我们采取每次弹射都弹射N跟光线，此时会发生指数爆炸

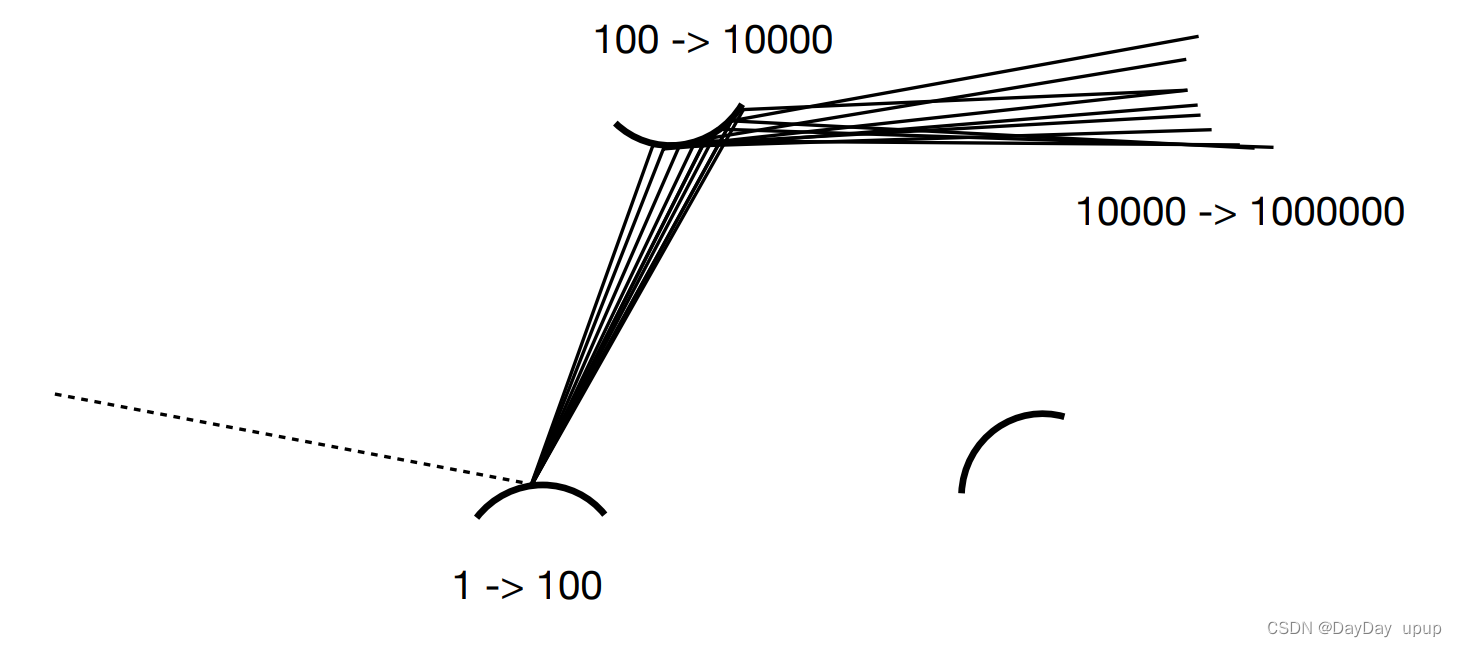
我们如何解决这个问题呢？
令N=1即可

但这样得到的图像噪声是很大的，我们仅需在一个像素内，打多根光线就行解决这个问题

问题2:这是一个递归的过程，递归的终止条件我们还没规定

解决方法1:我们人为的规定光线能弹射的最大次数，但这样做会有能量的损失，这里就不展开来说了

解决方法2:引入俄罗斯轮盘赌的方法
光线是否继续弹射，我们规定一个概率，从0到1进行随机选取一个数，若小于则继续进行光线的弹射

其实到这里，蒙特卡洛路径积分就已经完成了，为了加快收敛的速度，我们需选取更为合适的pdf

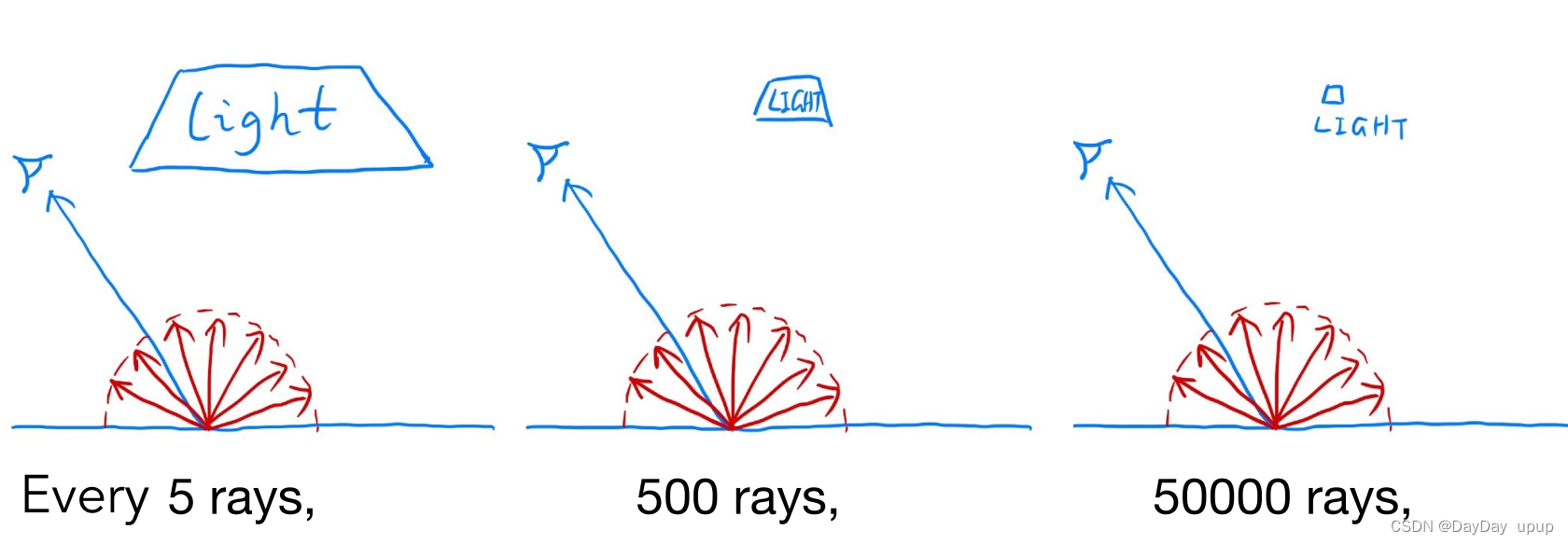
优化，对光源直接进行采样

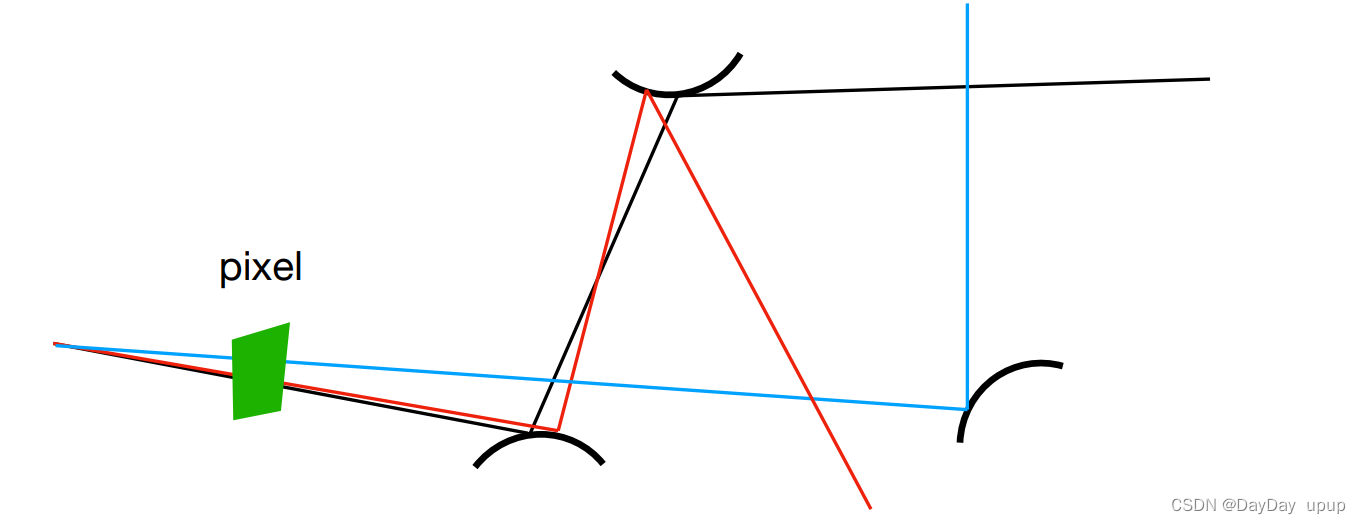
在下面这种情况下，当光源面积很大时，我们仅需很少的光线就能得到想要的效果，而当光源面积很小时，需要很多的光线才能打到光源，因此为了能尽快的打到光源，我们需要采取合适的pdf，直接对光源进行采样

因为蒙特卡洛积分要求对谁积分就要在谁上面进行采样，所以渲染方程进行改写，从对dω积分改为对dA积分，我们只需要知道dω和dA的关系然后替换即可。怎么替换？我们想想立体角的定义，面积除以距离平方，那我们只需要把dA这块面积投影到球面上然后除以着色点x和光源处点x’距离的平方即可，面积投影可以用cosθ’求得。而采样分布函数p(X)就是1/A，因为我们在光源上进行均匀的采样。这样一来我们就把渲染方程改为了对光源的积分。

这样我们就加速了积分的收敛速度