文章目录
- 前言
- 一、CRC校验原理
- 二、CRC实现
-
- 1.verilog实现
- 2.模块仿真
- 3.仿真波形
前言
现代数据通信要求信息传输具有高度可靠性 ,即误码率要足够低 。 然而 ,数据信号在传输过程中不可避免地会受到噪声干扰 ,或者信道不理想 ,从而造成的码间干扰而产生差错 ,即出现误码。 我们通常是通过一个校验码去判断接收的消息是否出现差错。信息在发送时,发送端会通过某个算法得到一个值,这个值被称为校验码。通信时发送端在发送消息时将校验码加在信息末端,接收端以相同的算法得到一个校验码,将发送端和接收端的校验码进行对比来判断是否正确接收到了信息。
提示:以下是本篇文章正文内容,下面案例可供参考
**【注意:】需要注意的是,CRC 软件计算结果与以太网使用时的关系为:
CRC 计算软件结果:低字节在前,高字节在后。
以太网使用时:高字节在前,低字节在后,即应以字节位为单位调换 4 个字节的高低顺序,如 BE7C1CBB 应该调换为 BB1C7CBE。**注意字节的使用顺序。
一、CRC校验原理
关于 CRC 校验能够降低数据链路通信出错概率的理论推导较长,这里为大家提供链接供大家下载学习。
链接:https://pan.baidu.com/s/18vUa-tnsxeIaqOEZoEO_sw?pwd=q0gn
提取码:q0gn
二、CRC实现
以太网报文校验字段 FCS 采用的是 CRC32 计算,关于 CRC 计算的 Verilog 代码实现已经做的很成熟,网上也有可直接生成 CRC 计算 Verilog 代码的网站。关于 CRC 计算原理感兴趣的可自行网上查找相关资料。这里主要是通过一个网站在线生成 CRC32 的 Verilog 代码,然后通过仿真对代码进行仿真验证。本例以千兆以太网的 GMII/RGMII 接口的 8 位数据模式为例进行介绍。
在线生成 CRC32 的 Verilog 代码的网站如下,点击进入网站是如下界面。
在线生成 CRC32 的 Verilog 代码的
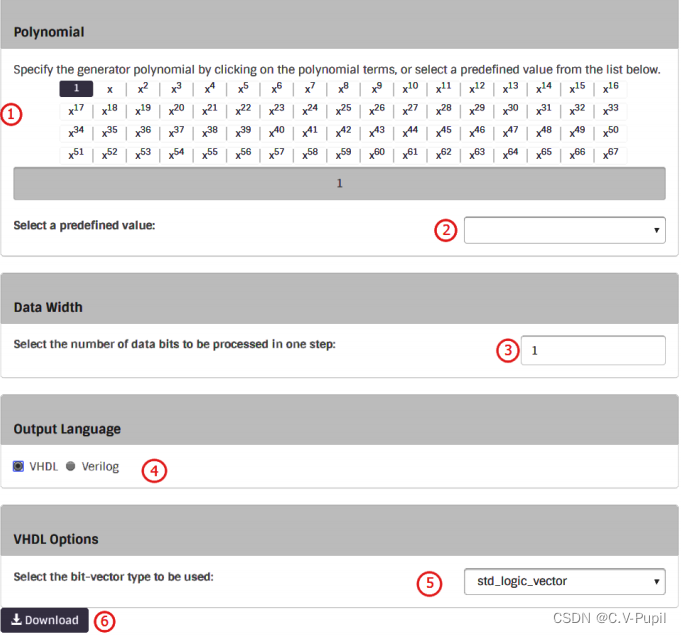
(1)CRC 生成多项式的设置,可根据多项式在窗口选择点击多项式中系数为 1 的 x 的
幂次方。比如这里的以太网的 CRC32 的多项式为 x32 + x26 + x23 + x22 + x16 + x12 + x11+ x10
- x8 + x7 + x5 + x4 + x2 + x + 1,则只需将 x32、x26 、x23、x22、x16、x12、x11、x10、x8、
x7、x5、x4、x2、x 、1 点击选择上,在窗口下方会根据你点击选择的 x 的幂次方会将 CRC
生成公式呈现出来,可与以太网的 CRC 生成多项式进行比较核对,确保多项式的设置没有
问题。

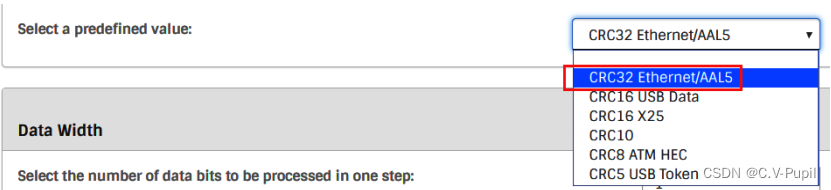
(2)这里同样是 CRC 生成多项式的设置,与步骤○1 不同的地方是这里提供了几个常用的 CRC 生成多项式供选择,对于以太网的 CRC 就直接在下拉框中选择 CRC32Ethernet/AAL5 即可,如下图所示。这里的不同的选择,同样会在步骤 1 中的窗口中同步更新显示,步骤 2 与步骤 1 都是 CRC 生成多项式的设置,步骤 1 更加灵活,可设置任意的CRC 生成多项式,而步骤 2 就只能选择几种常见多项式的中的一种。两个地方只要选择一个地方进行设置即可。
(3)设置输入数据流的位宽,如果是 MII 接口,则设置为 4,如果是用于 GMII/RGMII接口则设置为“8”。
(4)选择生成 HDL 代码的语言,选择“Verilog”。
(5)设置 VHDL 语言下要使用的位矢量类型,步骤 4 选择的是 Verilog 语言,就没有需要设置这个的地方。
(6)下载生成 Verilog 代码的入口,点击可进行下载。
配置完后的界面如下,这个网站设置后有时候更新很慢,需要等待一会时间。
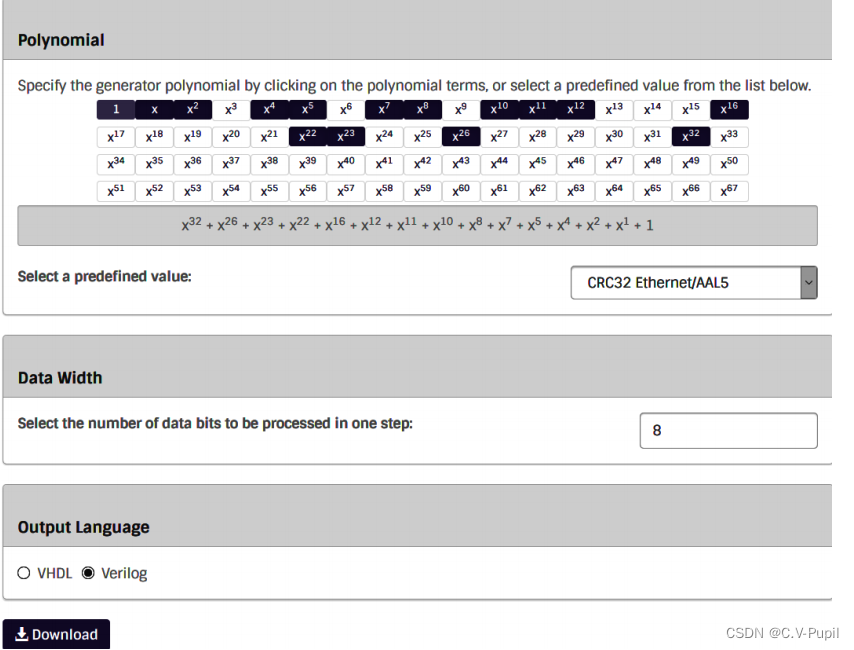
点击 Download,保存生成一个命名为 CRC32_D8 的代码文件,生成的具体代码如下。
// Copyright (C) 1999-2008 Easics NV.
// This source file may be used and distributed without restriction
// provided that this copyright statement is not removed from the file
// and that any derivative work contains the original copyright notice
// and the associated disclaimer.
//
// THIS SOURCE FILE IS PROVIDED "AS IS" AND WITHOUT ANY EXPRESS
// OR IMPLIED WARRANTIES, INCLUDING, WITHOUT LIMITATION, THE IMPLIED
// WARRANTIES OF MERCHANTIBILITY AND FITNESS FOR A PARTICULAR PURPOSE.
//
// Purpose : synthesizable CRC function
// * polynomial: x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x^1 + 1
// * data width: 8
//
// Info : tools@easics.be
// http://www.easics.com
module CRC32_D8;
// polynomial: x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x^1 + 1
// data width: 8
// convention: the first serial bit is D[7]
function [31:0] nextCRC32_D8;
input [7:0] Data;
input [31:0] crc;
reg [7:0] d;
reg [31:0] c;
reg [31:0] newcrc;
begin
d = Data;
c = crc;
newcrc[0] = d[6] ^ d[0] ^ c[24] ^ c[30];
newcrc[1] = d[7] ^ d[6] ^ d[1] ^ d[0] ^ c[24] ^ c[25] ^ c[30] ^ c[31];
newcrc[2] = d[7] ^ d[6] ^ d[2] ^ d[1] ^ d[0] ^ c[24] ^ c[25] ^ c[26] ^ c[30] ^ c[31];
newcrc[3] = d[7] ^ d[3] ^ d[2] ^ d[1] ^ c[25] ^ c[26] ^ c[27] ^ c[31];
newcrc[4] = d[6] ^ d[4] ^ d[3] ^ d[2] ^ d[0] ^ c[24] ^ c[26] ^ c[27] ^ c[28] ^ c[30];
newcrc[5] = d[7] ^ d[6] ^ d[5] ^ d[4] ^ d[3] ^ d[1] ^ d[0] ^ c[24] ^ c[25] ^ c[27] ^ c[28] ^ c[29] ^ c[30] ^ c[31];
newcrc[6] = d[7] ^ d[6] ^ d[5] ^ d[4] ^ d[2] ^ d[1] ^ c[25] ^ c[26] ^ c[28] ^ c[29] ^ c[30] ^ c[31];
newcrc[7] = d[7] ^ d[5] ^ d[3] ^ d[2] ^ d[0] ^ c[24] ^ c[26] ^ c[27] ^ c[29] ^ c[31];
newcrc[8] = d[4] ^ d[3] ^ d[1] ^ d[0] ^ c[0] ^ c[24] ^ c[25] ^ c[27] ^ c[28];
newcrc[9] = d[5] ^ d[4] ^ d[2] ^ d[1] ^ c[1] ^ c[25] ^ c[26] ^ c[28] ^ c[29];
newcrc[10] = d[5] ^ d[3] ^ d[2] ^ d[0] ^ c[2] ^ c[24] ^ c[26] ^ c[27] ^ c[29];
newcrc