论文笔记:SUPERVISED CONTRASTIVE REGRESSION_UQI-LIUWJ的博客-CSDN博客的loss function
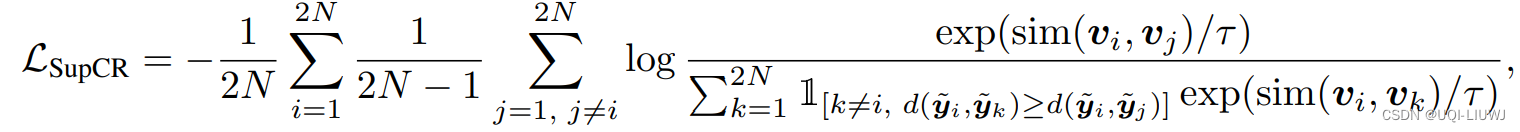
出于简单考虑,我们令v=y,同时sim就是两个向量的内积,d是两个向量逐元素差的绝对值之和
1 数据
import numpy as np
a=np.array([[1,3,4],
[2,3,7],
[4,0,-4],
[5,0,1]])
tau=0.52 相似度矩阵
similarity=np.dot(a,a.T)/tau
similarity
#第i,j个元素表示 第i行数据和第j行数据的相似度
'''
array([[ 52., 78., -24., 18.],
[ 78., 124., -40., 34.],
[-24., -40., 64., 32.],
[ 18., 34., 32., 52.]])
'''
exp_sim = np.exp(similarity)
exp_sim
'''
array([[3.83100800e+22, 7.49841700e+33, 3.77513454e-11, 6.56599691e+07],
[7.49841700e+33, 7.12058633e+53, 4.24835426e-18, 5.83461743e+14],
[3.77513454e-11, 4.24835426e-18, 6.23514908e+27, 7.89629602e+13],
[6.56599691e+07, 5.83461743e+14, 7.89629602e+13, 3.83100800e+22]])
'''
#exp_sim也即分子
numerator = exp_sim
numerator3 距离矩阵
n,m=a.shape
n,m
#(4, 3)
distance=np.abs(a.reshape(n,1,m)-a)
distance
#第i,j,k个元素的意义是:第i行和第j行第k个元素的距离
'''
array([[[ 0, 0, 0],
[ 1, 0, 3],
[ 3, 3, 8],
[ 4, 3, 3]],
[[ 1, 0, 3],
[ 0, 0, 0],
[ 2, 3, 11],
[ 3, 3, 6]],
[[ 3, 3, 8],
[ 2, 3, 11],
[ 0, 0, 0],
[ 1, 0, 5]],
[[ 4, 3, 3],
[ 3, 3, 6],
[ 1, 0, 5],
[ 0, 0, 0]]])
'''
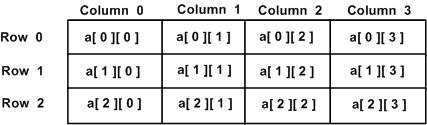
- 这里说一下思考过程,我们希望distance矩阵的第i,j,k个元素的意义是:第i行和第j行第k个元素的距离(我们统一用i表示三维矩阵第一个维度的下标,j表示第二个维度的下标,k表示第三个维度的下标)
- a.reshape(n,1,m)之后,第i,1,k个元素表示第i行数据的第k个值
- a是一个2维矩阵,和a.reshape(n,1,m)相加,根据广播机制,最前面要补一个维度
- 也就是自动被reshape成(1,n,m)维度,第1,j,k个元素表示第j行数据的第k个值
- 我们后面直接用a.reshape(1,n,m)表示a
- a.reshape(n,1,m)和a.reshape(1,n,m)还是不能直接相加,第一个张量的第二个维度需要复制n-1次,变成(n,n,m)维度;第二个张量的第一个维度需要复制n-1次,变成(n,n,m)维度
- 这两个复制后的矩阵相加,再加上abs(取绝对值操作),就得到了distance矩阵
- distance矩阵的第(i,j,k)个元素,是a.reshape(n,1,m)扩展到(n,n,m)的第(i,j,k)个元素,加上a.reshape(1,n,m)扩展到(n,n,m)的第(i,j,k)个元素
- a.reshape(n,1,m)扩展到(n,n,m)的第(i,j,k)个元素就是a.reshape(n,1,m)的第(i,1,k)个元素
- a.reshape(1,n,m)扩展到(n,n,m)的第(i,j,k)个元素就是a.reshape(1,n,m)的第1,j,k个元素
- ——>第i行数据的第k个值,减去第j行数据的第k个值
total_dis=np.sum(distance,axis=2)
total_dis
#第ij个元素就是第i行和第j行的距离,是一个对称矩阵
#每一对(i,j)的所有k加和
'''
array([[ 0, 4, 14, 10],
[ 4, 0, 16, 12],
[14, 16, 0, 6],
[10, 12, 6, 0]])
'''4 约束条件限制
4.1 k ≠ i
mask_i = np.eye(4) == 0
mask_i
'''
array([[False, True, True, True],
[ True, False, True, True],
[ True, True, False, True],
[ True, True, True, False]])
'''
mask_i=mask_i.reshape(n,1,n)
#第(i,1,k)个元素4.2 d(yi,yk)≤d(yi,yj)
dist_cond = total_dis.reshape(n,1, n) <= total_dis.reshape(n, n, 1)
dist_cond
'''
array([[[ True, True, True, True],
[False, True, True, True],
[False, False, True, False],
[False, False, True, True]],
[[ True, False, True, True],
[ True, True, True, True],
[False, False, True, False],
[False, False, True, True]],
[[ True, True, False, False],
[False, True, False, False],
[ True, True, True, True],
[ True, True, False, True]],
[[ True, True, False, False],
[False, True, False, False],
[ True, True, True, False],
[ True, True, True, True]]])
'''和前面广播类似的思考方法
dist_cond的第i,j,k个元素表示d(yi,yk)≤d(yi,yj)是否满足
total_dis.reshape(n, 1, n)的第i,1,k个元素表示d(yi,yk)
total_dis.reshape(n, n, 1)的第i,j,1个元素表示d(yi,yj)
total_dis.reshape(n, 1, n)≤total_dis.reshape(n, n, 1)就是d(yi,yk)≤d(yi,yj)
4.3 两个判断条件合并
indicator = np.logical_and(mask_i[:, np.newaxis, :], dist_cond)
indicator
'''
array([[[False, True, True, True],
[False, True, True, True],
[False, False, True, False],
[False, False, True, True]],
[[ True, False, True, True],
[ True, False, True, True],
[False, False, True, False],
[False, False, True, True]],
[[ True, True, False, False],
[False, True, False, False],
[ True, True, False, True],
[ True, True, False, True]],
[[ True, True, False, False],
[False, True, False, False],
[ True, True, True, False],
[ True, True, True, False]]])
'''5 计算分母
denominator = np.sum(indicator * exp_sim.reshape(n,1,n), axis=-1)
'''
array([[7.49841700e+33, 7.49841700e+33, 3.77513454e-11, 6.56599691e+07],
[7.49841700e+33, 7.49841700e+33, 4.24835426e-18, 5.83461743e+14],
[3.77513497e-11, 4.24835426e-18, 7.89629602e+13, 7.89629602e+13],
[5.83461808e+14, 5.83461743e+14, 6.62424768e+14, 6.62424768e+14]])
'''
- exp_sim.reshape(n,1,n) 表示
- 呈上indicator就是前面的那个条件不等式
- sum就是对k求和
6 计算最后的loss function
result_matrix = np.log(numerator / denominator)
result_matrix
'''
array([[-2.60000000e+01, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00],
[ 0.00000000e+00, 4.60000000e+01, 0.00000000e+00,
0.00000000e+00],
[-1.12535168e-07, 0.00000000e+00, 3.20000000e+01,
0.00000000e+00],
[-1.60000001e+01, 0.00000000e+00, -2.12692811e+00,
1.78730719e+01]])
'''loss=np.sum(result_matrix)
loss
#51.74614355460242
#对x轴和y轴求和